切片分析：小学数学教材分析新路径

基金项目：江苏省教育科学“十三五”规划重点资助课题“小学数学结构化学习的实践研究”（编号：R-a/2018/04）、江苏省教育科学“十三五”规划重点自筹课题“小学数学结构化学材开发的课例研究”（编号：B-b/2018/02/74）。

摘 要 我国小学数学教材有近十个版本，是非常好的教学研究参考资料。调查发现，广大中青年教师对不同版本教材资源的关注度并不高，不会研读教材是主因。从切片面包获得启示，采用切片法可以对教材进行较为深入的分析，化解问题。构建一课切片式教材分析框架，以“因数和倍数”为例，在三个版本教材切片分析比较基础上，统整教材资源，为教师研究教材提供参考途径。

关键词 切片式教材分析；框架建构；实例解读；教学实践

中图分类号 G623.5

文献标识码 A

文章编号 2095-5995（2022）04-0041-04

教材是学生获取知识的主要来源和教师教学的主要依据。^[1]教材资源效益最大化是教师专业素养的重要体现。目前，我国小学数学教材有近十个版本，给一线教师带来很大的学习研究空间。从丰富的教材资源中，博采众长，丰富“用教材去教”的理念，理应成为一线教师的行动自觉。“双减”时代，一线教师更要注重教材教法的深入研究，提高课堂教学效率。

一、问题的提出

2020年，笔者有幸参加江苏省某市A区乡村小学数学骨干教师培育站暑期培训和山东省某市B区小学高年级段数学教师暑期培训活动，对接受培训的教师进行现场调查，了解了两区教材的使用情况。两区使用的教材分别是苏教版、青岛版，手机现场扫码采集数据，共收到296份有效信息。通过数据分析，笔者发现：两区教师的教龄结构相似，其中21～30年教龄段人数占比最多，达32%，其余依次是4～10年、1～3年、11～20年，31年及以上最少，占8%。此外，调查显示，教师对教材研究存在如下问题：

（一）青年教师对不同版本教材的关注度需提高

从阅读不同版本教材人数占各教龄段人数的百分比看，经常阅读不同版本教材的教师为工作1～3年的年轻教师，A区经常阅读的教师占比19%，B区经常阅读的教师占比41.2%。把“经常”、“有时”两个选项的百分比相加可得：入职1～3年的教师对各版本的教材关注度也最高，A区占本段人群的52.3%，B区占本段人群的67.7%，远超过其他教龄段的教师。

（二）经常深入研读不同版本教材的教师不多

调查“您曾经深入地比较分析研究两种及以上不同版本教材的同一内容吗？” 两区调查结果较为相似，有近一半的教师没有深入研究分析不同版本的教材，其中研究不同版本教材的频次达到3次及以上的仅占15%～20%。

（三）研读教材没有成为教师教学设计智慧的重要来源

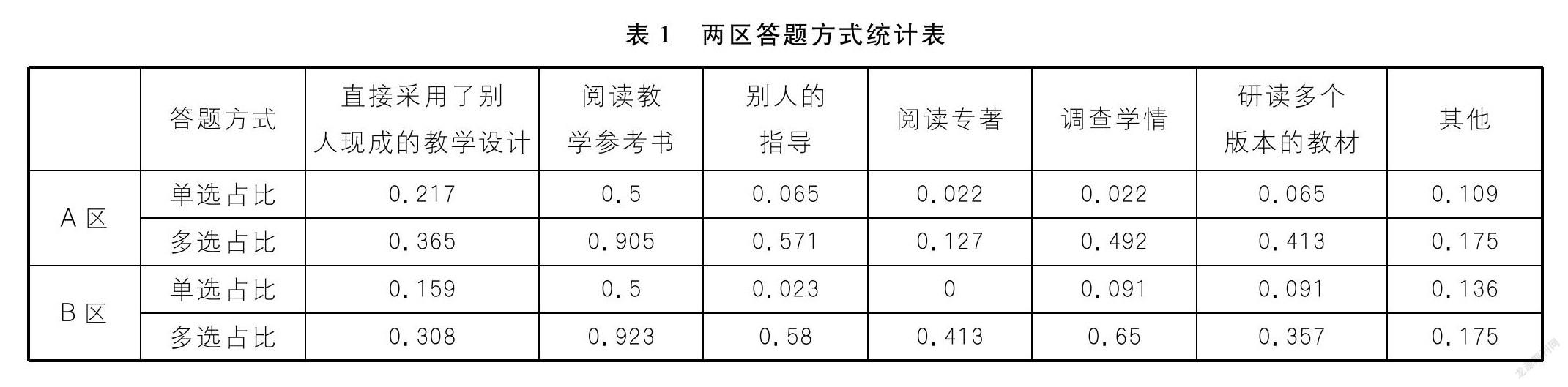
研读教材最显性的价值就是改进教学，有效促进学生发展。对于调查中“最近一次公开教学备课时，您的教学设计的灵感主要来自哪里？”这一问题，两区答题统计结果如表1所示。

在七种教学设计智慧来源中，“研读多个版本的教材”的回答占比居第五位，位次較低。在最近一次的公开教学中，仅有6.5%～9.1%（单选）的教师从研究多版教材中获得设计灵感；有35.7%～41.3%（多选）的教师选择多种策略，包含研读多版教材。

通过以上的调查发现，绝大部分教师没有深入地研究多版同类教材的经历，教材资源利用率低，通过访谈得知教师不会研读教材是主因。

二、切片式教材分析框架

（一）切片式教材分析内涵

数学教材如何研读？仁者见仁智者见智。生活是智慧之源，会给我们很多启示。切片面包是很多人的最爱，因为将一整块面包切开后，可以有多种吃法，随意取几片，可以蘸奶酪、番茄酱、果酱吃，中间也可以夹果蔬，夹煎蛋、培根等，根据自己的口味，丰富搭配，吃出个性。2000年后“一标多本”打破了“一本书教遍天下”的局面，教材呈百花齐放的态势。如何充分利用教材资源改善教学？

如果把一本教材中的一个单元、一课内容等看作一整块面包，根据编排内容的次序依次切开，每个切片就如面包的切片。对每个切片进行分析，充分研究后再进行加工，就如在面包中蘸酱、夹果蔬等进行个性化、深度理解的设计。如果对相同内容的两个版本及以上的教材用这种方法切开，进行横向比较分析，更深入地思考教学内容，这种研究教材的方法就叫“切片式”教材分析。这种教材分析法是把教材进行解构，切开后，再分析内部各元素之间、部分与整体之间的关系，然后重构教学。

（二）切片式教材分析框架

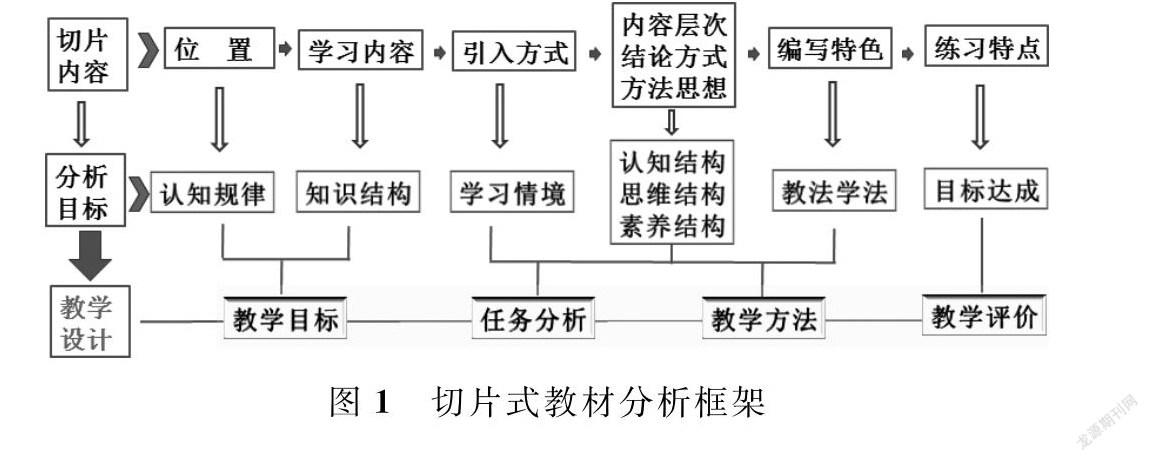
根据教学三要素：内容、学生和教师，切片式教材分析分为三个维度：切片内容、分析目标和教学设计。切片内容根据显性的教材编排顺序和隐性的方法思想，分为这几块：内容所处位置、学习内容、引入方式、内容层次结论方式及方法思想、编写特色和练习特点。根据结构化学学理分析的要素^[2]，分析目标可分为学生的认知规律、知识结构、学习情境、认知结构、思维结构、素养结构、表征结构等。现代教学设计是用系统化的方法将教学过程中的各元素进行结构化^[3]设计，设计主要分为教和学这两个系统，因此教学设计要关照教学目标、任务分析、教学方法和教学评价。根据解构与重构的结构观，可以按教材编排的顺序对教材进行切片分析，下面以一课时教学内容为例，构建切片式教材分析框架（如图1）。

三、切片式教材分析实例

（一）教材切片实例分析

以人教版小学数学教材五年级下册的“因数和倍数”这课为例进行切片分析。

1．切片的划分

人教版数学教材“因数和倍数”这课被切成七片，第一片是学习内容所处的位置；第二片是本课的学习内容；第三片是学习内容引入方式；第四、五、六片是学习内容展开的层次和方法思想；第七片是结论方式2。不同的学习内容，切片数量也存在差异，例如处在单元中间的内容，第二个切片在教材中不好切，则需要提炼；有的没有引入情境，如本课的例2和例3，则可以作为一大切片，然后将它再分项切成两至三个小切片来处理。

2．切片的分析

根据以上教材切片，下面重点对“引入方式”、“内容层次、方法思想”、“结论方式”这三个切片作以下分析：

（1）引入方式分析。在前面整数和小数除法的基础上，将9道除法算式进行分类，比较分类结果，进行归纳与概括。对除法算式分类时，是基于学生学习现状，从数学内在的逻辑结构展开，对接旧知，联系新知。

（2）内容层次与方法思想分析。本课有三个例题，即三个大的切片，每个例题在内容层次、方法思想方面存在紧密联系，例1是概念，例2、例3是概念的应用。例1的内容聚焦在除法分类结果中的第一类（整除），在归纳这类除法算式共同特点的基础上给因数和倍数下定义，然后用定义来阐释算式中两个数间的因数或倍数关系，体现了由具体到抽象再到具象应用的思想。例2和例3教材编排层次基本相同，注重介绍找一个数因数或倍数的策略——一一列举，这种策略渗透了集合思想。

（3）结论方式分析。结论主要指数学的概念、规律、公式、定理等，这些数学结论呈现的方式体现了对学生认知规律的尊重和数学结构发展的不断完善。本课有两个结论：一个是因数和倍数的概念，采用下定义的方式；另一个是一个数的因数或倍数的规律，采用不完全归纳法。下定义，纯文字是抽象的，对学生的理解能力要求高；归纳是基于具体的实例，有具象支撑，也可验证（具体分析见表2）。

（二）多版本教材切片对比分析

下面以“因数和倍数”这课为例，选择三个版本教材进行切片比较（如表2）。

（三）追问究理，统整教材的教学实践

1．反思追问

问题1：整除的概念有必要引入吗？整除是因数和倍数的上位概念，如果引入教学，则增加了学习任务量，也会增大难度，影响学生的学习动机。^[4]从以往的教学经验发现学生很容易混淆“谁能被谁整除”和“谁整除谁”。但是从知识整体性看，学生需要弄清“谁能被谁整除”和“谁整除谁”，这需要教师将整除概念的内涵向学生阐释清楚。

问题2：集合图要教学吗？必须渗透集合的思想吗？自然数、整数、因数和倍数的数学科学概念都是从集合论的角度来定义的，因此，教学中渗透集合思想是必需的。

问题3：枚举法是用乘法好、除法好、还是两种方法都用好？方法好不好可以从两个角度来判断：一是学生选不选，好不好用；二是两种方法是否都必须掌握。从方法的完整性来说，这两种都要教学，但选哪种？适合的才是最好的，由学生自己确定。

问题4：怎样培养学生的合情推理能力？合情推理在同类型同结构的情况下才易发生，所以推理前要丰富实例。

问题5：本课知识的本质是什么？因数和倍数两个概念的本质是非零自然数域内数与数之间的关系。

2．刨根究理

（1）数学科学概念。自然数是数学中最基本的概念，是指“一类等价的非空有限集合的标记，它表示非空有限集合中元素的个数”^[5]，或“有限集合的基数”^[6]。这两种界定方式大同小异，都是从集合论的角度来界定，此外还有公理化的界定。在几种自然数的界定中，这种集合论的界定与小学生能理解的描述性定义关系更近一些。因此，某些版本教材的编写者就从自然数作为数学科学概念的角度在此部分教材中呈现了集合图，以渗透集合思想。

因数与倍数是数论中的基本概念，数论中的因数与倍数的定义为：“如果整数a能被自然数b整除，那么a叫做b的倍数，b叫做a的约数，约数有时也叫因数。”^[7]还有一种定义为：“对于整数a与b（b≠0），如果存在一个整数q使a=bq成立，那么称b整除a，记为b│a。这时a称为b的倍数 ，b称为a的约数或因数。”^[8]前一种定义中“整除”是属概念，是因数和倍数概念的根，后一种定义则是将相乘关系作为属概念，整数是研究数的范围。在以上三个版本的教材中，人教版教材主要依据前一种定义来介绍因数和倍数，其他两个版本教材则根据后一种定义引入因数和倍数。从小学生当前的认知水平看，在学习此内容之前学生已有丰富的乘法和除法运算基础，但乘、除两种运算中，乘法属于顺向思维，所以对于因数和倍数的界定，后一种方式更利于小学生理解和掌握。

（2）课程标准中相关内容的表述。与本课内容相关的教学标准有：在1～100的自然数中，能找出10以内自然数的所有倍数，能找出一个自然数的所有因数，了解自然数、整数等。^[9]在数学思考方面，与本课联系紧密的有：在一系列思维活动中，发展合情推理能力，独立、有条理地思考，清楚表达思考过程与结果。体会数学的基本思想。^[10]在情感态度方面的要求则为：“在运用数学知识和方法解决问题的过程中，认识数学的价值。”^[11]

（3）教材单元知识结构。梳理教材知识结构（如图2），我们会发现本课学习的基础是整数的乘、除法，整除是因数与倍数的根概念，因数与倍数又是后面其他知识学习的核心概念，因此乘除法（积、商）是学生认识和掌握因数倍数的桥梁（图2）。

3．统整教材的教学实践

在教材切片分析和学理分析的基础上，统整三个版本教材资源，设计教学可以充分发挥教材资源的作用，优势互补，对教师的教学设计进行适当的充实与完善。这样获得的“因数和倍数”的教学思路如下：画出12个小正方形拼成的长方形——描述乘除法算式中的因数与倍数关系——任意两数间的关系——引导学生通过反例——找因数及规律——找倍数及规律——实践情境演练。在教学实践中，我们会发现：学生在判断任意两个数因数和倍数关系时，明显比直接根据乘、除法算式思考的时间要长，学生思考时十分依赖乘、除法算式，在说算理的过程中，学生想乘法算式的人数明显比想除法的要多得多。学生只要想出了算式，就能判断两数间的关系；反例的学习可以促进学生正确建构核心概念，激发学生学习主动性。

切片式教材分析是分析教材的一个新视角和新方法，通过纵、横分析与比较，教师可以更深入地理解教材，发现差异，通过深入思考发现知识间的内在逻辑关系。这样，教师就可以根据学生的认知结构设计出适合学生学习、有自己独特理解的教学流程，在提高教师自身专业素养的同时促进学生更好地发展。切片式教材分析的框架只是按教材本身的编排顺序进行初步的建构，操作容易，但它的合理性、科学性还有待在实践中进一步完善。

（毛文波，南京市金陵小学，南京 210046）

参考文献：

[1] 邵瑞珍.教育心理學[M]．上海：上海教育出版社，1988：392．

[2] 吴玉国.小学数学结构化学习的实践研究[M]．南京：江苏凤凰教育出版社，2021：19-22．

[3] 毛文波，吴玉国. 备课轴：小学数学结构化学习的实务[J].中小学教师培训，2018（12）：62-66.

[4] 邵瑞珍等.教育心理学——学与教的原理 [M]．上海：上海教育出版社，1983：290．

[5][7] 江苏省中等师范学校教材编写组.小学数学基础理论[M]．南京：江苏教育出版社，1987：2，69．

[6][8] 洪修仁.小学数学基础理论[M]．苏州：苏州大学出版社，1995：54，119．

[9][10][11] 中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

责任编辑：刘 源