初中数学例题变式教学的实践与认识

蒋媛

【摘  要】本文对初中数学例题变式教学的实践进行探究。首先，概述初中数学例题变式教学的原则，包括目的性原则、启发性原则；其次，分析例题变式教学的作用；最后，从概念教学、习题教学、复习教学三个角度出发，列举例题变式教学的实践策略。

【关键词】初中数学；例题变式；教学

一、初中数学例题变式教学的原则

近年来，在初中数学课堂教学中，有很多教师对例题变式教学活动进行了一系列的探索与尝试，取得了宝贵的经验，经验表明，遵循以下原则进行例题变式教学，可使例题变式教学取得最佳成效。

（一）目的性教学原则

例题变式教学中，教师多数情况下都会使用现成材料进行课堂教学，如针对教材中出示的例题，设置变式题目进行课堂教学。教师有必要遵循目的性教学原则，完成教学工作，將现有的资料，以多种方式进行灵活变化，形成更具针对性、创新性的例题，吸引学生的注意力。结合教学需求，采用多种新颖的教学模式，为学生讲解例题及变式题，使课堂变得更丰富多彩，活跃学生的学习思维，缓解学生的学习疲劳，最大化发挥例题变式教学的效果。为达到以上教学目的，教师有必要在备课环节中，仔细分析题目特点，找到变式方向，如此便可使变式题教学真正成为数学教学的助推力，促进学生的成长和发展。

（二）启发性教学原则

以循循善诱的启发性教学方式，引导学生进行自主探究式学习，是课程改革倡导的教学思路。教师应遵循启发式教学原则，开展例题变式教学。在日常授课过程中，教师应结合学生的学习需求、学习能力、思维特点甚至兴趣爱好，选择具体的例题变式教学方法，循序渐进、潜移默化地带领学生借助变式题，巩固数形知识、技能，提升学生的学习质量，推动学生数学学习水平的持续进步。

二、初中数学例题变式教学的作用

（一）有利于帮助学生克服思维定势

长期学习数学学科后，学生往往会形成一定的思维定势，这种思维定势通常指的是一种固化的思维习惯。大量研究及实例证明，人脑的认识活动常受“经验”的影响，有时人们会因这种经验的影响而走入误区，这便是思维定势为人们带来的不利影响，若无法及时察觉这种思维定势，人们的思考会变得因循守旧、生搬硬套，细化到数学解题领域中，就是学生常会因思维定势的蒙蔽，走入解题的误区。教师可借助例题变式教学，解决以上问题，减少思维定势为学生带来的影响，使学生的学习思维变得更科学、严谨，鼓励学生开阔思路，使学生逐渐形成良好的思维习惯。

（二）有利于培养学生的发散思维能力

培育学生的发散思维能力，使学生解题思维变得更为变通，这也有助于提升学生的数学学习水平。初中生正处青春期，大脑尚在发育，可塑性强，教师可借助例题变式教学，开发学生的潜能，促进学生发散思维能力及创新能力的成长发展。例如，教师可从例题的情境、条件等角度出发，给予例题灵活的变化，从多视角切入，考查学生对不同知识的掌握情况，使学生形成挑战欲望，激发学生的学习积极性，拓展学生的发散思维能力。此外，现阶段看来，初中数学课堂中，进行例题变式教学的价值，还在于能够彰显数学学科的本质，能够帮助学生更为明确地察觉题目给出的干扰项，对数学知识的本质产生明确认识，这同样也有助于拓宽学生的发散思维，使学生在学习时能举一反三、灵活变通。

三、初中数学例题变式教学的实践策略

（一）概念教学中的变式教学

概念教学是数学教学的基础。目前看来，初中课堂中，很多学生背诵数学公式十分熟练，却对概念的理解十分肤浅，在使用这些数学基础知识进行解题时，常会遇到瓶颈，若教师给予变式题，这些学生很难顺利完成“举一反三”。为解决以上问题，使这类学生真正领会数学概念的核心意义，教师应重视在概念教学中，为学生设计一系列的变式题，将概念还原到真实的数学模型或数学情境中，为学生呈现有针对性的变式题，供学生进行探索，使数学概念的内涵变得更为清晰、明确，使学生更好地经历知识体系在脑海中构建而成的全过程，突破概念教学瓶颈。

以对“相似三角形”这一知识内容的教学为例。教师可为学生出示两个全等三角形△ABC、△DEF，并提出问题：这两个三角形是全等三角形吗？你是如何判断的？你认为满足什么特征的两个三角形，可被称作全等三角形？引导学生对这些问题展开思索。之后教师可为学生拿出两张大小不同的中国地图，提问学生这两张地图有怎样的关系？接着为学生展示两个大小不同的等边三角形，引导学生分析“全等三角形”的特点。最后，教师可为学生展示两组相似三角形，鼓励学生走上台来，以直尺等工具，测量两个三角形，分析“相似三角形”的内涵，明确相似三角形的判断定理，掌握概念的核心特征。

又如在教学“平面直角坐标系”这一知识点时，教师可针对例题，为学生设计变式题：

（1）x轴上有一点P（a，b），求b的值是多少；若点P位于y轴上，求a的值是多少；若点P与0点重合，求a、b的值分别是多少。

（2）若点P位于第一象限，求a与b的取值范围。若条件不变，P位于第三象限呢？

（3）求点P（-3，1）到x轴、y轴、原点的距离。

（4）若点P到x轴距离为5，到y轴距离为4，且点P位于第二象限，写出点P的坐标。

（5）已知点P坐标为（3，-6），现有一点关于x轴与点P对称，写出该点坐标；还有一点关于y轴与点P对称，写出该点坐标。

教师可依据教学需求及学生的学习情况，精心设计层层递进、由浅入深的变式题，训练学生的思维，让学生感受到通过自主探究，一步步探明数学概念的满足感与成就感，升华学生对核心概念的理解，增强学生的解题能力，培育学生的思维品质。

（二）例题教学中的变式教学

现阶段来看，数学教材给出的例题极具典型性，对学生而言，有良好的潜能开发价值。在教学过程中，若教师仅沿用传统教学手段，让学生孤立、静止地解答这些习题，学生获得的学习体验，也仅是使用学过的数学知识，解决了一个问题而已。但如果教师能够指引学生对例题展开深入研究，通过一题多解、一题多变等方式，挖掘题目更为深刻的学习价值，长此以往，学生思维的灵活性与深刻性将会得到质的提升，教学成效会更加显著。同时，在教学过程中，为学生设计恰当合理的变式题目，也有助于在课堂中营造出民主、活跃、宽松的学习氛围，使学生对数学知识产生一定的亲近感，这有利于减小学生的学习压力，培育学生的创新精神，使学生逐步形成从多视角出发、自主探究数学题目的意识、习惯与能力。

原题：如图1所示，已知四边形ABCD为平行四边形，AF与CH、DE与BG长度相等，EG与HF互相平分吗？为什么？

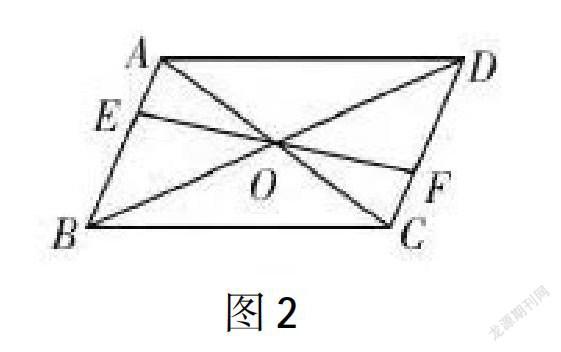
变式1：如图2所示，已知四边形ABCD为平行四边形，O为对角线AC与BD的交点，现作一线过点O，交AB、CD于点E、点F，OE与OF长度相等吗？为什么？

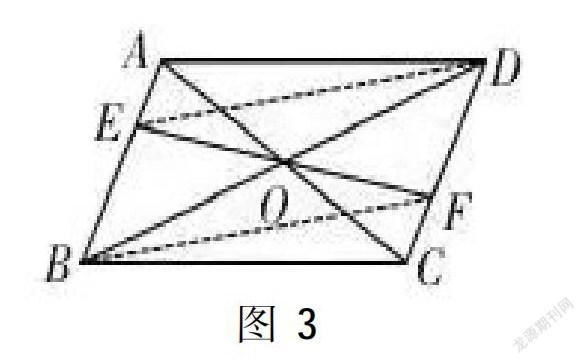
变式2：连接图2中哪些线段，可构成新的平行四边形？图3、图4出示了两種构成新的平行四边形的方法，请证明四边形EBFD、AECF为平行四边形。

变式3：图2中， 若过点O，再作一线段GH， 分别交AD、BC于点G和点H （图5） ， 可得到哪些新的平行四边形，为什么？

在上题组中，教师对题目的条件、结论、背景给予了层层递进的变化，为学生提供了一系列丰富多样的变式题，从不同角度出发，考查了学生对课堂所学知识的掌握情况，这有利于使学生形成灵活的数学解题思维，提升学生的学习水平。

（三）复习教学中的变式教学

复习课在初中数学课堂教学中有重要的作用。在课程改革背景下，教师应积极思索传统复习课的不足，将复习课真正视作深化、提升学生学习思维的重要环节，精选习题，给予学生有针对性的变式训练，指导学生从更高层次出发，进一步思索自己学过的数学知识，夯实知识、技能储备。

例如在教学完“全等三角形”一课后，教师可为学生设计变式题：

问题：在△ABC中，有AB=AC，BD与CE为三角形角平分线，求证BD=CE。

教师可设计以下的变式题：（1）你能够用不同方法证明BD=CE吗？（2）原题目中，若已知条件不变，可得出哪些结论？（3）能否在改变已知条件的情况下，证得BD=CE？（4）请你同时改变已知条件与结论，甚至改变图形，利用学过的知识点，对题目进行一定的改编，并自己回答问题。

以上的变式题，体现了教师与学生对“全等三角形”相关题目的创新，实践证明有良好的课堂教学效果。在数学课堂教学中，教师应重视革新问题情境与问题条件，使题目变得更为新颖，培养学生“举一反三”的思维习惯。但应注意，为“变式”而“变式”，设计形式僵化的数学题也是不妥当的，教师应遵循目的性原则，结合教学目标设计变式题，确保变式题与学生的学习需求一致，力求激发学生思维的积极性与创造性，使学生活学活用、学以致用地学习数学知识，彰显数学知识的本质属性，培养学生的知识应用能力、发散思维能力与创新能力，促进学生的进步发展。

四、结束语

综上所述，在初中数学课堂教学中，围绕教材给出的例题，为学生设计一系列的变式题目，有重要的意义。教师应为例题变式教学制订明确的目标，结合学生的学习基础、学习需求，围绕例题，给予学生一系列层层递进的变式题目，发展学生的数学思维能力，促进学生的持续成长。

【参考文献】

[1]许道娒.“变式教学活动”在初中数学例题教学中的组织设计[J].教育界，2020（27）：50-51.

[2]胡安红.初中数学教学中变式题的应用技巧探究[J].新智慧，2019（3）：32.

[3]吴玉龙.掌握初中数学变式题组，提升复习课学习效果[J].现代中学生（初中版），2021（6）：25-26.