基于多轮升维策略与改进量子行为粒子群优化算法的热导率函数估计方法
席振翔, 于 帆
(北京科技大学 能源与环境工程学院,北京 100083)
1 引 言
根据测得的温度场反演材料随温度变化的热导率是一类典型的热传导反问题IHCP(inverse heat conduction problem),在各类工业领域广泛存在[1,2]。IHCP属于不适定问题,较小的输入误差可能造成反演结果精度骤降,不恰当的初值也会使得算法无法获得有效结果。受限于测温技术,测量误差无法避免,这就要求解决方案能在一定的输入误差下稳定工作,同时,若解决方案过多依赖于初值或是搜索范围的选取,则会大大降低其有效性。
对于热导率反演问题,国内外学者提出的求解方法主要可分为梯度类方法与随机类方法。梯度类方法主要包括Levenberg-Marquardt算法[3]、伴随方程法[4]和共轭梯度法[5]等,此类方法收敛速度快,计算结果精度高,但会涉及到灵敏度矩阵的计算,且初值敏感度高,无法跳出局部极值点。随机类方法中应用最广泛的为遗传算法[6],该方法具有较强的全局搜索能力,对搜索范围的要求相对较低,但收敛速度缓慢。在先验信息不足且同时反演的热导率参数较多的情况下,即便是全局搜索能力较强的随机类方法也难以得出有效结果。
为解决以上问题,本文将一种改进的量子行为粒子群优化算法应用于高温隔热材料热导率函数估计问题中,并提出了一种多轮升维策略提升算法在该问题的搜索效率。
2 正问题
为确定材料热导率而开展的实验往往会设置一个加热面,通过大功率加热使得试件升温,而非加热面既可以安装隔热材料防止热量散失,也可以使其暴露于空气中。经过一段时间的加热,获取试件上各测点的温度数据,以此来反演材料随温度变化的热导率。本文考虑材料除上下表面外的四个端面为绝热,在一维变物性、无源项和瞬态导热问题中讨论算法性能,其控制方程可表示为
(1)
初始条件为
t=0∶T(y,t)=T0
(2)
边界条件为y=0∶T=f(t)
(3)

由外节点法将目标区域离散为有限个网格,采用有限差分法推导时间隐式离散方程,并由三对角阵算法求解即可获得各节点处的温度值。
3 反问题
3.1 反问题的优化目标函数
在反问题中,优化目标函数设置为测点温度计算值与测量值之间的残差,即
(4)
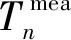
x=(x1,x2,…,xD)=(λ1,λ2,…,λD)
(5)
将热导率离散为常数从而进行反演的方法称为热导率的函数估计方法(function estimation approach),本文将待反演的温度范围均分成多个温度区间,x的每一分量对应某一温度区间端点的热导率值,温度区间内热导率值由温度区间端点处热导率值线性插值获得。
3.2 改进的量子行为粒子群优化算法
粒子群优化PSO(particle swarm optimization)算法是一种基于种群的高性能优化技术[7],在IHCP领域已经得到了广泛应用,并在一些传统方法失效的情况下得以证明,PSO算法也能取得良好的数值结果[8]。在标准的PSO基础上,Sun等[9,10]从量子力学的角度提出了量子行为粒子群优化QPSO(quantum-behavior particle swarm optimization)算法,并通过实验结果证明了QPSO算法收敛性能相比于PSO算法以及遗传算法有了很大的提升。QPSO算法的粒子进化方程可表示为
xi,k + 1=ai,k±α|mk-xi,k|∘ln(1/ui,k)
(6)
式中xi,k为第i个粒子在第k代时的位置,α为收缩扩张系数,ui,k为0~1上均匀分布的随机变量组成的向量,ai,k为局部吸引子,mk为第k代的平均最好位置,∘为两向量对应元素分别相乘。
ai,k=φi,k∘pi,k+(e-φi,k)∘gk
(7)
式中pi,k为第i个粒子在第k代时的个体最佳位置,gk为第k次迭代时的种群最佳位置,φi,k为 0~1上均匀分布的随机变量组成的向量,e为与φi,k同维的单位向量。
(8)
式中N为种群规模。
对于最小化问题,当k>0时,pi,k与gk按如下方法确定,
(9)
(10,11)
本文式(6)的参数α采用自适应策略[11],相比于普遍采用的线性递减策略[9],该策略能使QPSO的收敛速度明显提高。其实现方法如下,
αk=C1-C2sk+C3jk
(12)
式中C1,C2和C3均为常数,分别取为1,0.4和0.1;sk与jk分别为进化速度因子和聚集度因子。
在寻找极小值的问题中,当k>0时,sk与jk的计算方法为
sk=F(gk)/F(gk - 1)
(13)
(14)
为了增加算法的全局搜索能力,合理利用多核处理器资源,本文基于多种群协同搜索策略[12]构建一种粗粒度并行模型,将整个粒子群划分为多个子种群,每个子种群由多核CPU的一个核进行独立计算,再按照一定的交流概率共享部分信息。其交流概率计算为
qk=(k/K)z
(15)
式中K为迭代总次数,z取0.8。
采用以上改进策略的QPSO算法即为多种群并行自适应量子行为粒子群优化算法,即MAQPSO算法,其具有较强全局搜索能力,适合于处理高维问题。采用MAQPSO算法反演热导率的计算流程如下。
(1) 置k=0,在搜索范围(xmin,xmax)内初始化各粒子群中粒子位置xi,0,置pi,0=xi,0,由式(8)计算m0,由式(4)计算F(xi,0),由式(10,11)确定g0。
(2) 由式(15)计算qk,产生(0,1)内均匀分布的随机数μk,若μk (3) 若k=0,置α0=1;否则,分别由式(13,14)计算进化速度因子sk与聚集度因子jk,再由式(12)计算收缩扩张因子αk。 (4) 由式(7)计算局部吸引子ai,k,由式(6)更新粒子位置xi,k + 1,由式(4)计算F(xi,k + 1),由式(9~11)确定pi,k + 1与gk + 1,由式(8)计算mk + 1。 (5) 若k+1 在反演较大温度跨度下的材料热导率时,为了更细致地捕捉热导率随温度的变化规律,往往会划分更小的温度区间对热导率进行离散,这意味着更高的反演维度,这时即便采用上述MAQPSO算法,也难以在较少迭代次数下获得有效结果。 热导率反演也存在初值敏感度问题,梯度类算法虽然有更高的计算效率,但其计算表现却严重依赖于初值的选取,且初值敏感度会随着反演参数个数以及测量误差水平的增加而增加。相比之下,基于种群的随机类算法仅需输入一个搜索范围,这使得此类方法在材料先验信息不足的情况下有着天然的优势。然而在较高的反演维度下,过大的搜索范围也会使得随机类算法收敛速度大大降低。 为了解决以上问题,本文将MAQPSO的反演过程划分为M轮(记m为反演轮次,dm与Km分别为第m轮反演的维度与最大迭代次数),dm从低到高逐轮提升,并在最后一轮开始时达到目标维度。在每轮反演结束后将粒子的位置x通过线性插值转化为下一轮反演的粒子初始位置,而个体最佳位置p与种群最佳位置g也做同样的处理。 图1 多轮升维策略实现方式Fig.1 Multi -round upgrading strategy implementation 即除了首轮反演中粒子位置需要在迭代前进行随机初始化以外,后续轮次反演开始时均继承上一轮反演搜索到的有用信息。以上策略基于材料热导率随温度变化相对连续的特点,利用算法在低维空间中获取的信息指导高维搜索,从实现上来说则是在搜索过程中多次对粒子的位置信息进行插值,使得搜索进程由低维向高维推进。 c(T)=1013+0.75×10-3T2 (16) 用离散数据点表示在300 K~1300 K的范围内热导率随温度的变化,计算中将热导率看作分段线性函数,每25 K取一个温度节点,由41个离散数据点组成的向量即为待反演变量x的精确解。 一维模型为真实实验的简化模型,在y=b面,取h=10 W/(m2·K),Tf=300 K,而在y=0面进行大功率加热,其温度随时间变化为 (17) (18) 在较大的搜索范围下测试MAQPSO算法的搜索能力,取xmax=100,由于真实热导率值总大于0,取xmin=0,采用4个种群并行计算,每个种群的粒子数为10。基于多轮升维策略,将算法的反演过程分为4轮,d1~d4分别取2,6,21和41,K1~K4分别取30,30,30和50。 定义平均相对误差,以描述反演结果的误差水平为 (19) 本文数值实验环境为MATLAB R2019a,Intel(R) Core(TM) i7-6700HQ CPU@2.60GHz,为了便于对比,每次计算均固定ω,即在同一套测量噪音下进行数值实验。 图2 不同σ下热导率的反演结果Fig.2 Inversion results of thermal conductivity with different σ 图3 不同σ下利用反演结果计算出来的测点温度变化历程与其测量值比较Fig.3 Comparison of temperature history calculated with estimated thermal conductivity and experimental value under different σ 当σ=0,2%,4%和6%,反演结果的平均相对误差分别为2.172%,3.058%,2.773%和3.157%。可以看出,算法在不同误差水平下都能得到有效结果,且对测量误差的敏感度较低,随着σ增加,计算结果偏离精确解的程度略有增加。 将热导率真值设为分段函数,忽略了系统误差的影响,理想情况下,若σ=0,式(4)的值可降低至0。为研究系统误差带来的影响,热导率真值改为由以下随温度变化的连续函数获得 λ(T)=0.5exp(T/1500)+0.2sin(T/150) (20) 而算法反演时仍将热导率看作分段线性函数,以此来产生系统误差,在这种情况下,即便σ=0,式(4)的值也无法降低至0,精确解与反演结果如图4所示。 图4 不同σ下λ(T)的反演结果Fig.4 Inversion results of λ(T) with different σ 可以看出,在存在系统误差的情况下,算法仍能较好地捕捉热导率随温度的变化,反演结果在较低σ下与真值的函数曲线符合良好。随着σ增加,剩余的目标函数值增加,当σ=0,2%,4%和6%,反演结果的目标函数值分别为0.092,4.591,9.180和13.771,反演结果逐渐散布在了真值两侧。 将MAQPSO算法与PSO和QPSO算法进行比较,分别取xmax为1,10,100和1000,σ=2%,总粒子数为40,迭代总次数为140,热导率真值设为以分段线性函数表示的材料真实热导率,算法将反演300 K~1300 K下41个离散热导率参数值(图2 中Exact),按是否采用多轮升维策略分为两组,若采用该策略,各轮次迭代的反演维度与次数设置同4.1节。 PSO算法为采用了惯性权重线性递减策略的标准粒子群算法,其惯性权重值随着迭代次数的增加从0.9线性减小至0.6,设置粒子的运动速度上限vmax=0.1xmax,学习因子c1=c2=1.5。 QPSO算法中α采用线性递减策略,其值随着迭代次数的增加从0.8线性减小至0.5;MAQPSO算法的设置与4.1节相同。 两组数值实验中,同一搜索范围下各算法均采用同一随机数种子初始化种群,使得各算法在同一搜索范围下有相同的起点。不同搜索范围下的初始目标函数值Finitial、最终目标函数值Ffinal、反演结果的平均相对误差Emr以及算法总运行时间列入表1和表2。 表1 未采用多轮升维策略时各算法的反演结果Tab.1 Inversion results of each algorithm without using multi-round upgrading strategy 表2 采用多轮升维策略时各算法的反演结果Tab.2 Inversion results of each algorithm using multi-round upgrading strategy 由表1可知,在未采用多轮升维策略时,各算法均无法高效处理41个热导率分量。随着搜索范围增大,剩余的目标函数值也增大,即便在(0,1)的范围中进行搜索,各算法所得结果也均无法满足工程应用的要求。 由表2可知,采用了多轮升维策略后,各算法的搜索效率明显提高,在(0,1)的搜索范围下,PSO、QPSO和MAQPSO算法均在140次迭代后获得了有效结果,如图5所示。可以看出,即便是采用了多轮升维策略,随着搜索范围的加大,PSO算法的结果质量也逐渐下滑,当xmax=1000时,仅有采用了多轮升维策略的QPSO与MAQPSO算法能在140次迭代中获得有效结果,且PSO算法在使用时需要设置粒子运动速度范围,不恰当的vmax也会影响算法收敛,这限制了传统粒子群优化算法的工程应用。采用多轮升维策略的QPSO与MAQPSO算法在不同搜索范围下的计算结果如图6和图7所示,可以看出,其反演结果几乎不受搜索范围的影响。 图5 不同算法在(0,1)搜索范围下的反演结果Fig.5 Thermal conductivity inversion results obtained by different algorithms in the search range of (0,1) 图6 基于多轮升维策略的QPSO算法在不同xmax下的反演结果Fig.6 Thermal conductivity inversion results of QPSO algorithm based on multi-round upgrading strategy at different xmax 图7 基于多轮升维策略的MAQPSO算法在不同xmax下的反演结果Fig.7 Thermal conductivity inversion results of MAQPSO algorithm based on multi -round upgrading strategy at different xmax 由表2可知,当采用了多轮升维策略后,MAQPSO算法的反演精度略低于QPSO算法,其部分原因在于多轮升维策略使得该问题对算法全局搜索能力的要求降低。但从耗时上考虑,MAQPSO算法的并行计算方式使其能够利用多核处理器资源,相比于PSO和QPSO算法有着更短的计算时间。 本文将一种改进的量子行为粒子群算法应用于热导率函数估计问题中,并提出了一种多轮升维策略提升粒子群优化算法在该问题中的搜索性能。通过数值实验讨论了测量误差以及系统误差对算法反演结果的影响,并分析了不同粒子群优化算法在该问题下的表现,得到的主要结论如下。 (1) 基于多轮升维策略的MAQPSO算法能在单个测点下同时反演多个热导率参数,对搜索范围以及测量误差的敏感度较低。 (2) 多轮升维策略对PSO、QPSO和MAQPSO算法在热导率函数估计问题的计算表现均有较大提升,但使用该策略后的PSO算法对搜索范围仍然较为敏感,相比之下,QPSO和MAQPSO算法有更佳的计算表现。3.3 基于热导率函数估计的多轮升维策略

4 仿真实验与讨论
4.1 仿真实验条件与算法设置

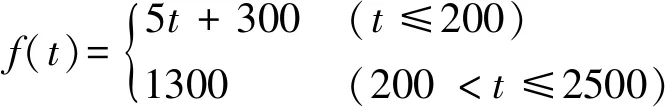
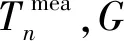
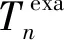
4.2 测量误差及系统误差下的反演结果
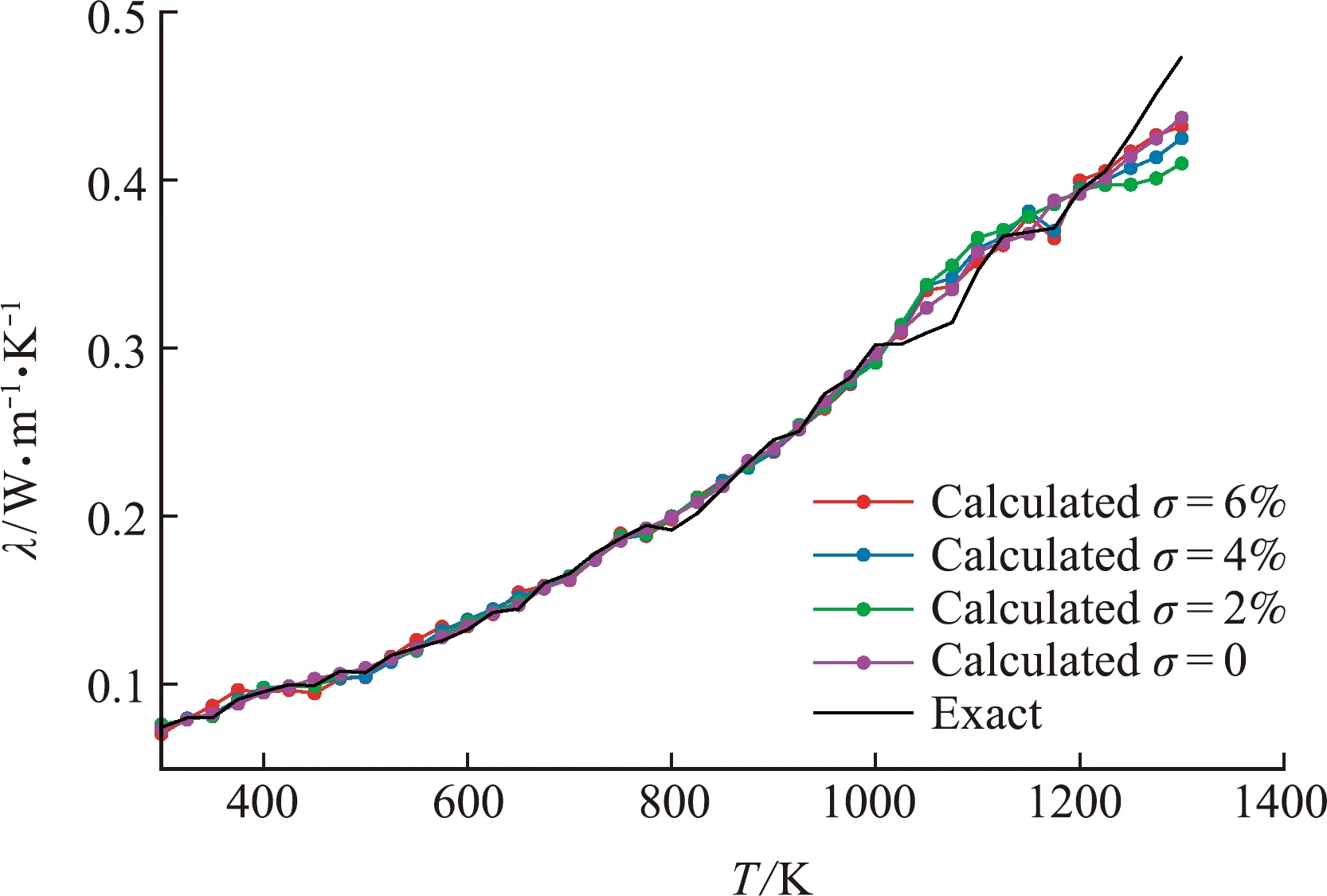
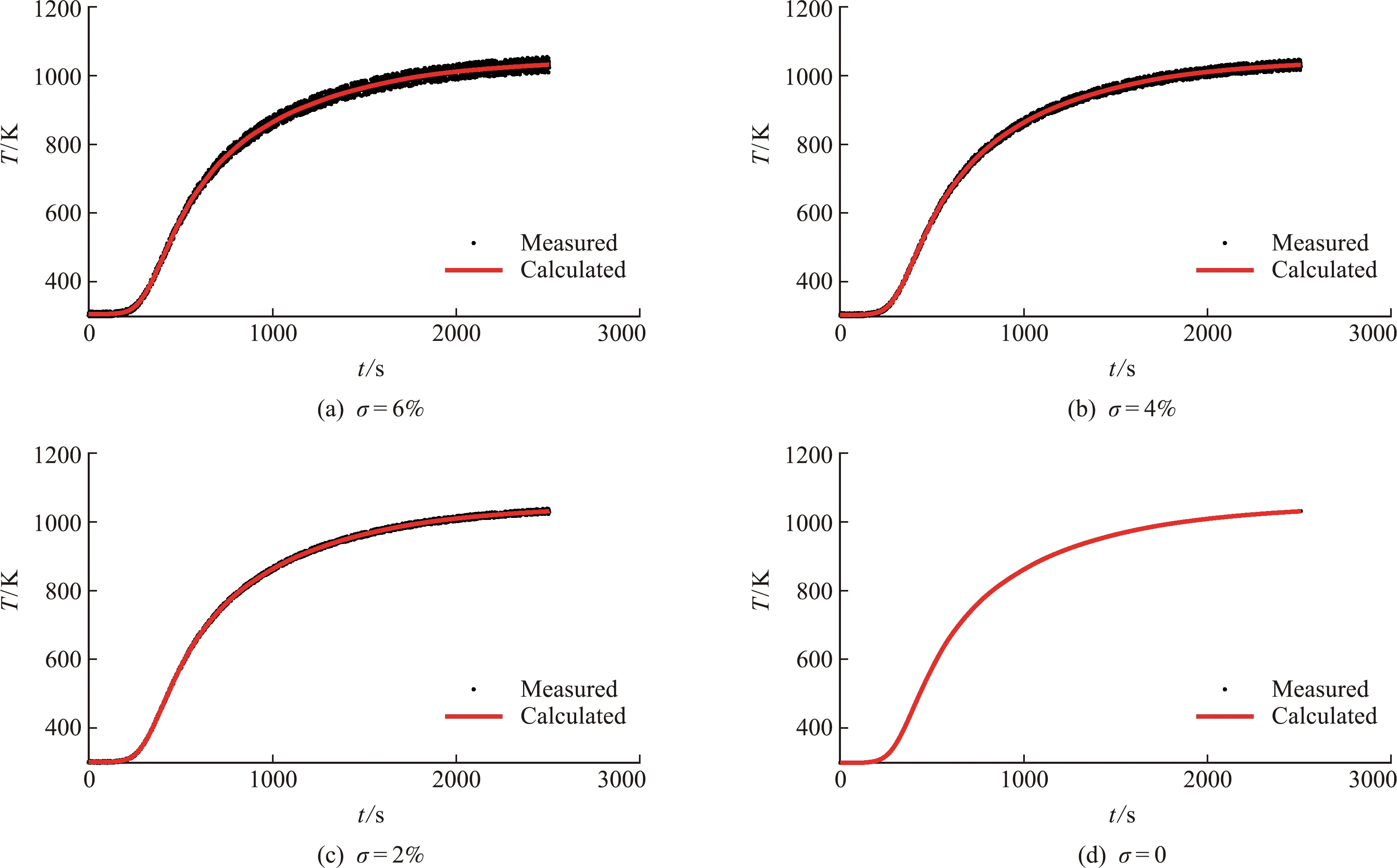
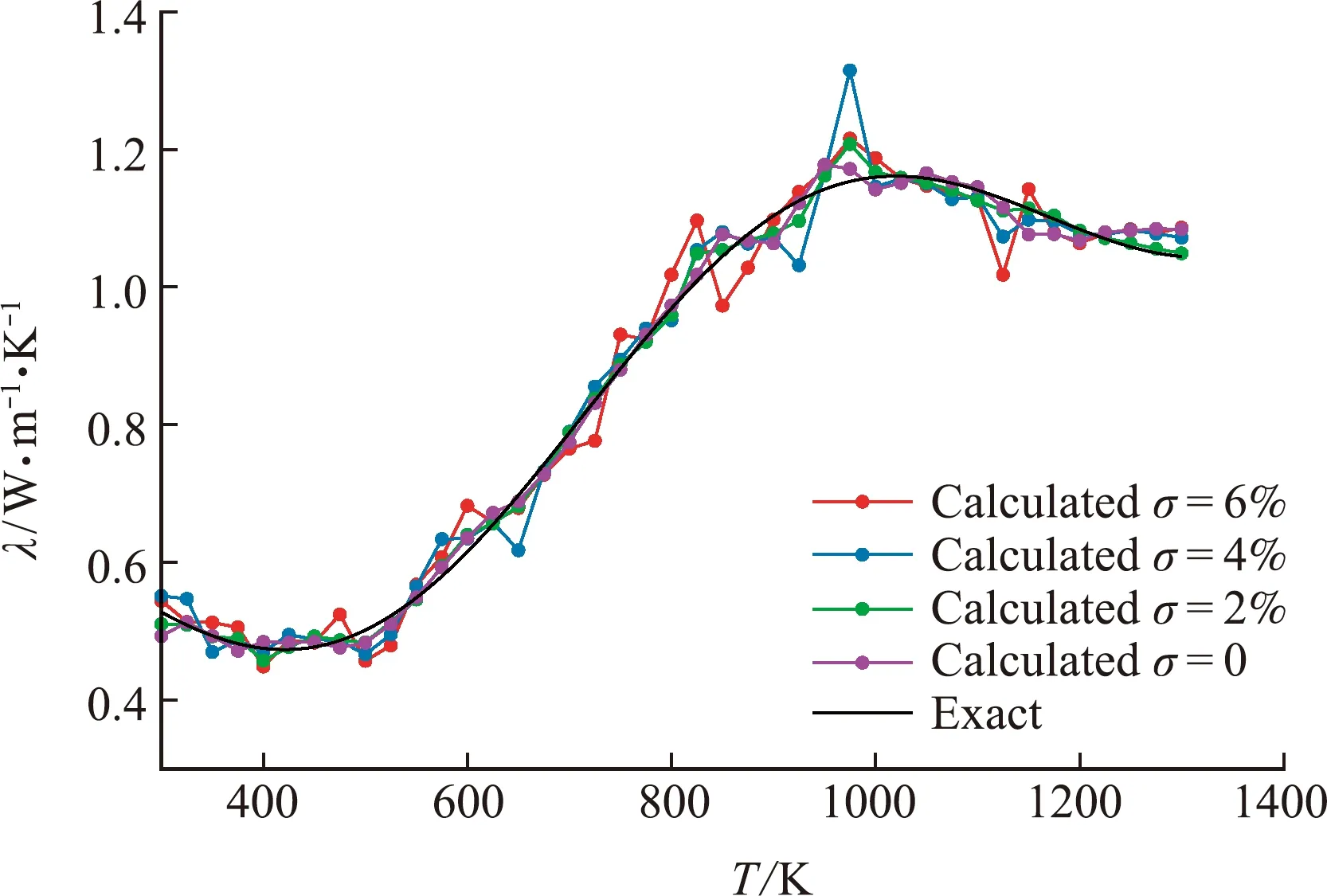
4.3 多轮升维策略对算法的影响
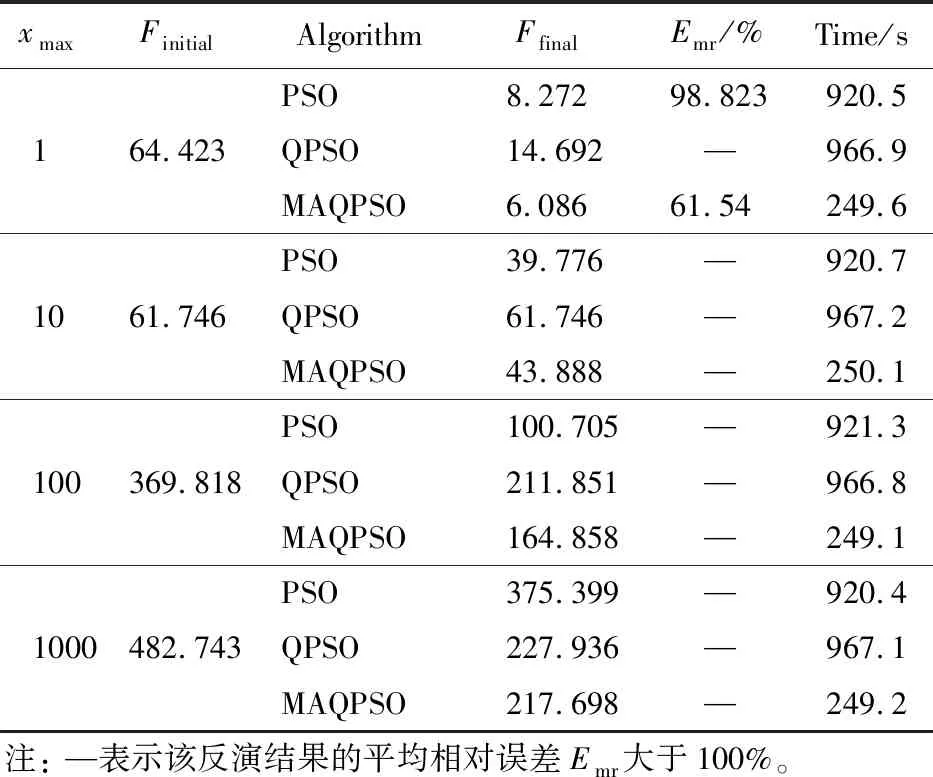
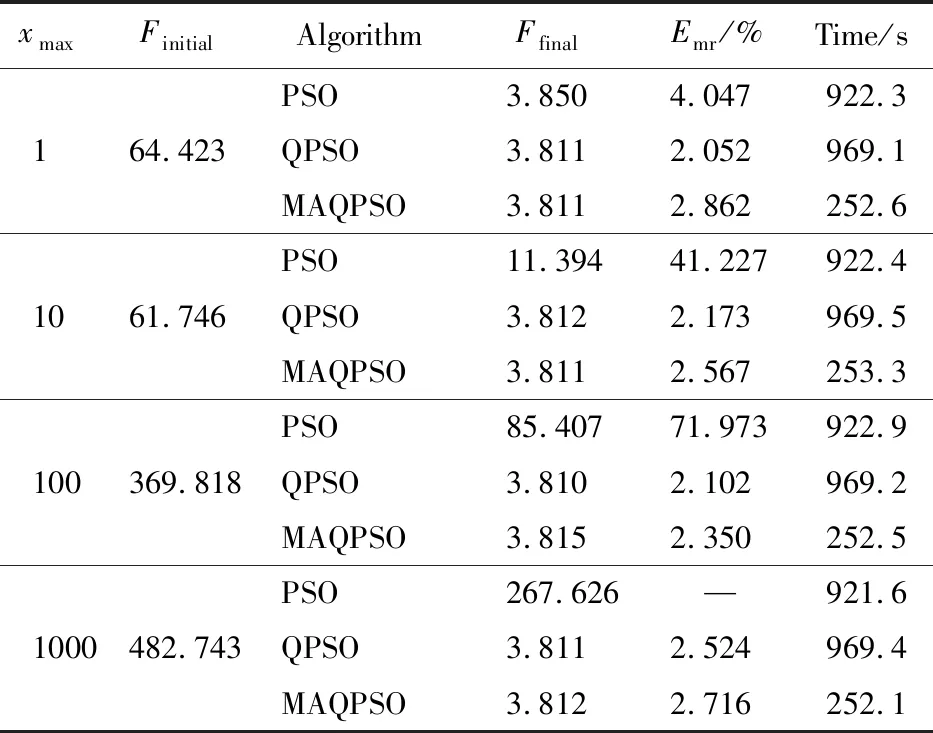

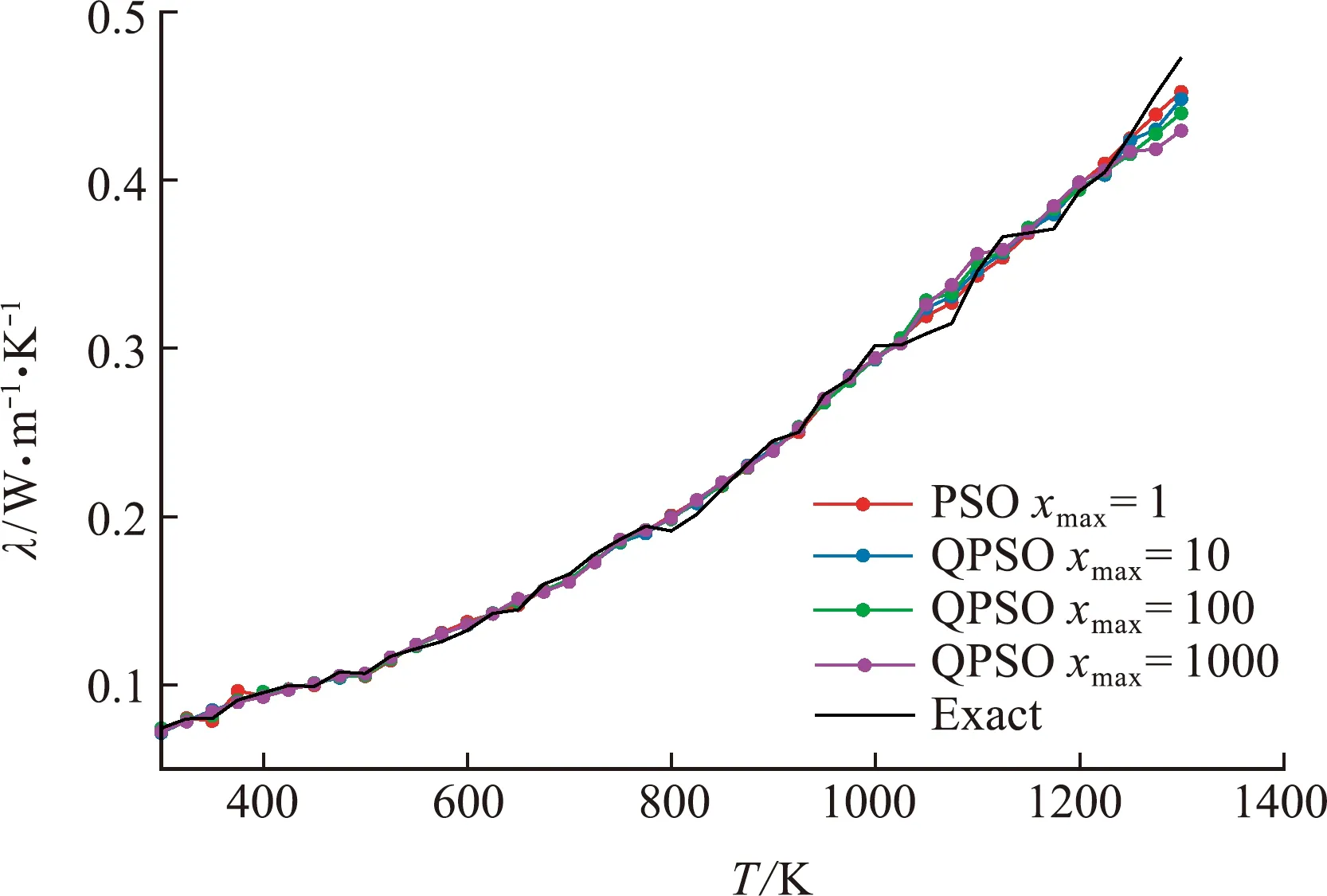

5 结 论

