回归教材起始点 抢占备考制高点
杨海涛 (江苏省盐城市建湖高级中学 224700)
将2021年高考数学全国卷Ⅰ试题与中学教科书做针对性的详细对照可以发现,试卷中有相当数量的试题可以在高中教科书中找到它们的影子,这些“影子”对于解决这些高考试题有着至关重要的作用:夯实基础,以不变应万变.新高考卷用不争的考题证明:盲目做题、过度刷题,不但增加学生的学习负担,而且也无益于学生高考成绩的提高.这对于引导师生放弃题海战术,将更多的精力放在研读教科书和探究典型题型上,具有十分重要的意义.新一届乃至以后的高三复习备考都必须遵循回归教材、紧抓典型例题、深入研究的原则.从教材原点走向备考的制高点才是高考复习备考的王道.
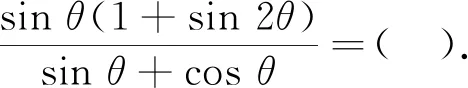
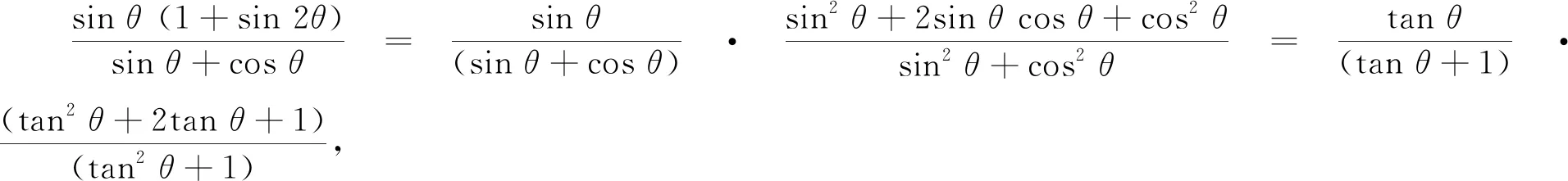
评注上面的分式实际上是可以进一步化简的,但我们认为,该分式能化简只是一种偶然现象,且不关乎问题处置的本质(因为此时已可直接代入计算而无任何实质性困难了).事实上,教科书中类似问题有不少,比如:

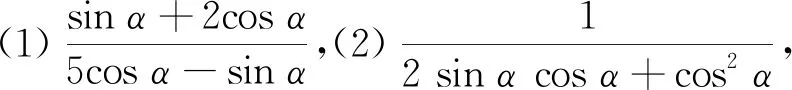
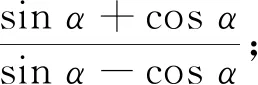
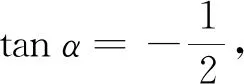
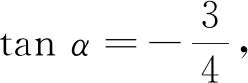
(2)2sin2α+ 3sinαcosα-cos2α.
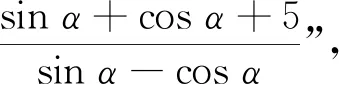
例2(2021年全国卷Ⅰ第13题) 已知函数f(x)=x3(a·2x-2-x)是偶函数,则a=;

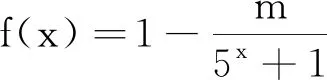
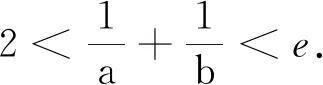
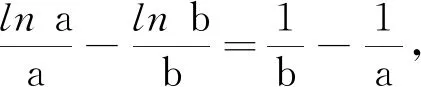
例3(2021年全国卷Ⅰ第19题)记△ABC的内角A,B,C的对边分别为a,b,c,已知b2=ac,点D在边AC上,BDsin∠ABC=asinC.(1)证明:BD=b;(2)若AD=2DC,求cos∠ABC.
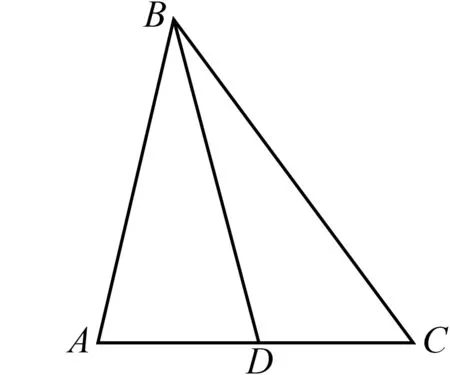
图1
命题要害剖析与简解我们不妨将这种由一个顶点(比如点B)和其对边上一点(如点D)连结起来的三角形称为“λ型三角形”.很显然,我们熟知的三角形中线长问题、内角平分线定理都是这类以λ型三角形为背景的问题.这类题目的破解关键就在用好联系三角形△ABD及△BCD的桥梁——边BD及互补角∠BDA与∠BDC(这两个角的正弦相等,从而可以联系正弦定理,同时这两个角的余弦互为相反数,又可联系余弦定理),于是本题可简证如下:
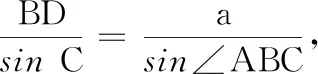

评注数学核心素养的“数学抽象”水平要求学生能将已知命题推广到更一般的情形中[4].此类问题的一般情形称为斯台沃特定理.与此题密切相关的教材问题有:
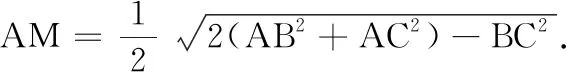
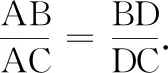
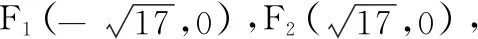


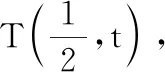
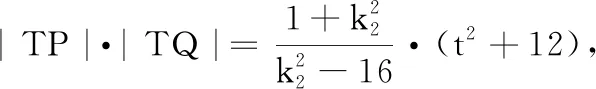
评注对这道题的第(2)问,这里还是采用了大多数考生常用的直角坐标系求解的思路,未采用直线的参数方程办法,化简工作量不小,上面已经充分注意到几何结构关系的对称(注意:这种对称不是我们传统意义上的镜面对称)特征,简化了书写过程,依然较繁.类似问题如下:
问题1(人教2019A版选择性必修第一册[1]第120页例2)已知A,B两地相距800 m,在A地听到炮弹爆炸声比在B地晚2 s,且声速为340 m/s,求炮弹爆炸点的轨迹方程.
综上所述,我们能够体会到命题人的初心就是希望师生回归课本.事实上,像这样关涉到教材典型例题的高考真题,除了上面提到的,还有很多.如第10题引入教材中的两角和与差的三角函数的典型情境、第16题的第二空其实就是错位相减法的应用,这些知识在教材中都有明显的展示.限于篇幅,感兴趣的读者可自行对照研究.

