“学生说题”的基本要素与教育意义
王柳娟 (浙江省云和县中等职业技术学校 323600)
所谓学生说题,就是在课堂教学中,针对某一题目或主题“请学生当老师”,让学生将自己审题、分析、解题和反思的思维过程,以口头语言及相关辅助手段的形式呈现给教师和其他学生的活动.让学生说题,就是一个调动大脑及各种感官去获得与生成知识、方法和能力的过程.如果说,学生的思考过程是第一思维过程,那么,说题就是学生第二思维过程的暴露.
1 学生说题的基本要素
1.1 追根溯源说题意
分析命题是理解题目的核心,是解题的第一步,同时是有效说题的前提[1].解题,首先是通熟题意,吃透题中各个条件及关系是展开思维的基础.说清题意主要包括说题目所给的条件是什么,要解决什么问题,题中涉及哪些数学概念、理论变化和规律等知识点,以及这些知识点之间的联系,即通常所说的审题.找准题目中的关键词,挖掘其中的隐含条件,说出本题涉及的知识点及命题意图等.
·说条件和结论
在解题时,让学生厘清题目条件和结论,说明白题中所给的条件及其相互关系,特别是挖掘出题目所隐含的条件,由已知条件可以得出哪些结论,借此获取条件和结论之间的逻辑关系.
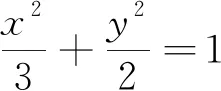
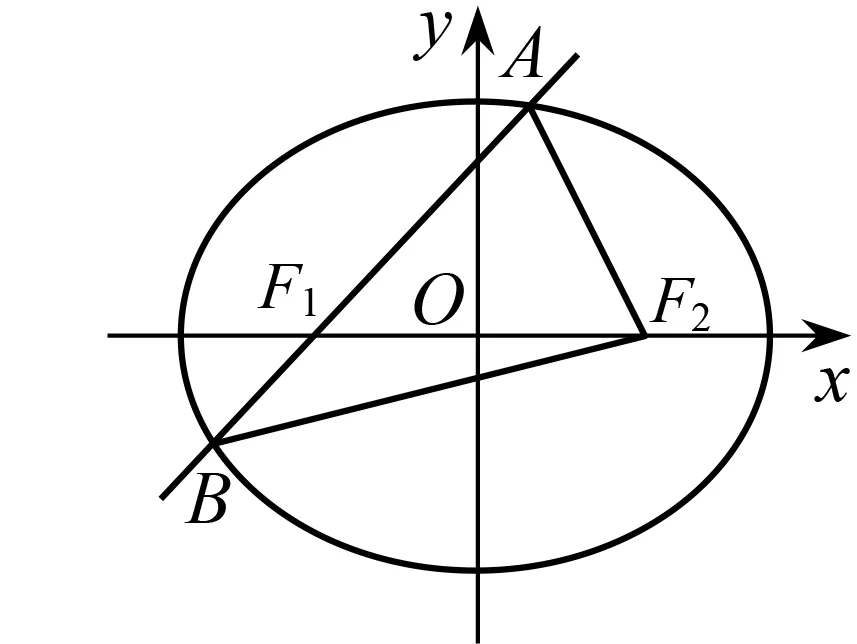
图1
(1)试说明△ABF2的周长为定值,并求此定值;
(2)若直线l的倾斜角为45°,求△ABF2的面积.
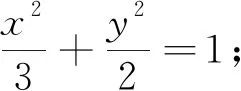
得出结论尚需解决的问题是:(1)焦点坐标;(2)直线方程;(3)弦AB的长;(4)△ABF2的高.
说清题目的条件与结论,才能明白目标指向,知道从何处下手,向何处突破.
·说命题意图
每一道习题中都蕴含着相关的知识、原理、规律及数学思想方法等,只有明确习题的命题意图——考查的学科知识、方法、能力、觉悟,才能找到问题的出发点和归宿.布鲁纳的发现学习理论认为:“认识是一个过程,而不是一种产品.”通过学生说命题意图这一环节,让学生追根溯源,领会习题的命题意图,明确题目考察的学习目标,能促使学生对相应问题进行有效的迁移和化归.
教师要引导学生围绕以下几个方面说出它的命题意图:(1)这是什么类型的题目?(2)问题涉及的知识点有哪些?(3)命题的目的是什么?考察了哪些能力?
通过说命题意图,学生明白例1是一道直线与圆锥曲线(椭圆)的综合题,考查了直线和椭圆的相关知识,包括直线方程、椭圆的定义、标准方程、弦长、点到直线的距离公式等知识点的应用,同时还考查了学生分析和解决问题的能力,重点提升数学抽象、逻辑推理、数学运算等核心素养.
1.2 有理有据说思路
罗增儒教授曾说:“分析典型例题的解题过程是学会解题的有效途径”.解题思路是一个由已知到结论的推理过程,是由线索到真相的分析.疏通解题思路正是学生实现知识生长、能力提升的关键点[2].说解题思路即说出问题的解决步骤、思考过程、所用的数学知识和思维方法,确定解题策略,提炼思想方法.通过说思路,让学生的思维过程外部言语化,在其最近发展区,基于抽象思考和形象表达,暴露思维过程,不仅“知其然”且“知其所以然”,达到诊断、交流和调控的目的.同时,通过“说”的形式,学生的思维能力和语言表达能力也得到了训练.说解题思路是数学说题的关键.
在例1中,学生能否从结论(1)“说明△ABF2的周长为定值,并求此定值”的问题,联想到椭圆的定义“到两个定点距离之和等于定长”是解题的关键.圆锥曲线的定义是描述动点满足的本质特征,实际是动态中的定值,它既是有关圆锥曲线问题的出发点,又是新知识、新思维的生长点.通过说思路,有利于学生重新审视概念,回归定义,合理选择运算思路和解题方法,建立解决直线与圆锥曲线问题的解题策略和思想方法.
1.3 刨根问底说感悟
美国数学教育家波利亚在《怎样解题》中把解题分为四个阶段:“弄清问题、拟定计划、实现计划、回顾与反思”.[3]回顾与反思就是回顾解题过程,是对解题活动深层次的再思考、再认识,是对自己的解题过程重新审视、总结规律的过程.反思的目的不仅仅是为了回顾过去,更重要的是指向未来的活动.
学习过程中,学生的数学思维和解题思路是逐步培养出来的,教师要鼓励学生把心里话说出来,引导学生进行解题反思,并大胆地表达自己的感悟:(1)为什么这样做?依据是什么?(2)蕴含哪些思想方法?(3)还有其他解法吗?这些方法能否优化?(4)在解题及思考过程中应该注意些什么?还存在哪些问题?(5)通过说题,你有什么收获?
让学生带着这些问题“回头看”,总结解题方法、规律,去思考感悟相关知识之间的内在联系,及时调整思维策略和解题方向,构建自身的数学认知结构,提高综合运用数学思想方法分析、解决问题的能力,并在潜移默化中,逐步养成解题反思的习惯和意识,提高解题反思的能力.
1.4 举一反三说变式
对例习题进行一题多变的学习研究,是训练学生高阶思维、促进深度学习的有效路径.此处的变式是在学生充分认识问题本质的基础上,在自己的最近发展区内编制拓展的新试题.一般来说,变式应该源于原题并高于原题,且具有导向性和层次性.
例如,有学生在说题时对以下原题进行了变式拓展:
例2过抛物线y2=2px焦点的一条直线与这条抛物线相交,两个交点的纵坐标分别为y1,y2,求证:y1y2=-p2.

变式2 过抛物线y2=2px对称轴上的点M(a,0)的一条直线与抛物线相交于两点A(x1,y1),B(x2,y2),求证:x1x2=a2,y1y2=-2pa.
该生通过类比分析,结合例2的证明过程,对原题进行了变式拓展,变式1对原题的结论进行改编,变式2根据特殊到一般的思维方式,将“过焦点”推广到“过对称轴上任一点”,使问题深化到较高层次,进行了数学学习的“再创造”,对课堂学习的知识进行了有效的拓展和延伸.
1.5 把握脉络说关联
世间万物总是相互依存、相互影响的,学习也是一样.有学者认为:“没有关联就没有学习,学习是因关联而存在的”.无论是数学知识的获得、思想方法的体验还是活动经验的积累都不是碎片化的,而是相互关联,是存在于一定的情境脉络之中的[4].结合前面四个环节中具体问题的解决,进一步挖掘彼此之间联系,寻找知识内容、思想方法之间的关联性,捋清思维脉络、形成通性通法,并通过改进和优化,得到新的思路和方法,达到更高水平的数学认知和发展.通过说数学关联,有利于建立良好的认知结构,梳理通法,发现新法,形成“知识块,方法链”.
2 学生说题的教育意义
2.1 充分暴露思维过程
说题能展现其思维过程并及时纠正其思维偏差.学生做题一般只能表达出解题过程和结果,不能完全暴露其思维过程,说题教学能弥补这一不足,充分暴露学生的思维过程,进一步提升学生思维品质,同时,有利于教师帮助学生从根本上纠正问题.说题,让教与学更加明白.
2.2 促进学生深度学习
说题能挖掘学生潜力,培养其思维能力.说题教学使学生在师生交流中各抒己见、互献智慧,在磨炼中探索、尝试和验证,进行思维方式的沟通,以达到集思广益和突破创新的目的,培养学生思维的深刻性、广阔性、创造性乃至批判性,深入挖掘学生的潜在能力,促进学生深度学习.说题,让教与学更有深度.
2.3 培养数学交流技能
数学作为一种科学语言已被用于人类社会的几乎所有领域.因此,数学交流也就成为现代公民的一种基本技能.由于数学知识、方法、推理等都是用数学语言表述的,在说题过程中,学生经历了数学语言与自然语言之间的翻译转换,能运用数学语言正确、迅速、规范地表达解题过程,用数学概念、原理及思想方法解释一些自然和社会现象等等.[5]逻辑严密、语言严谨,在有效促进数学理解的同时,推进数学交流技能的形成和发展,学会用数学的思维思考问题、用数学的语言表达世界,是提升中学生能力、发展核心素养的“润滑油”和“催化剂”.说题,让教与学更加生动.
2.4 全面增强学习自信
说题为学生搭建了展示自我的平台,学生在说题中能充分展示自我,并提高学习兴趣和学习效率.学生由被动学习变为主动学习、主动参与,体现了其主体地位,每个学生都有展示才华的机会,使学生在良好的教学情境中以最佳心理状态和思维状态学习交流,不仅提升思维能力、表达能力,更是增强了学习自信.说题,让教与学更加温暖.
说题是把以学生为本的理念具体化,是教育教学实践中提炼出来的一种新型双边教学模式,是探讨解题方法、提炼数学思想、探寻总结解题规律、提高分析问题和解决问题能力、优化思维品质的重要举措,具有很强的可操作性.它是学生摆脱题海战术,培养良好的数学素养及语言表达能力,充分暴露解题思维的过程,有利于学生良好思维品质的养成和核心素养的提高.
——张奠宙,于波.数学教育的“中国道路”[M].上海:上海教育出版社,2013:121.

