以“实践+分析”有效培育学生“四基”
——以一堂函数列表课为例
沈 浩
(江苏省苏州中学,江苏苏州,215007)
1 课程背景与意图
从教育部深化高中课程改革的要求来看,高中除注重学科知识的掌握和运用以外,更应该消除侧重应试教育这一弊病.从学生健康发展的内部需要来看,学生个体对个性化、多样化发展的需求日益强烈[1].
《普通高中数学课程标准(2017年版)》在内容标准部分,将数学探究、数学建模与数学文化作为独立的部分呈现,阐述了各自的内涵、教育价值,并提出了要求,对如何实施给出了说明和建议.数学探究、数学建模作为一种新的学习方式引入高中数学课程,旨在为学生提供自主学习、探究学习的空间,使学生经历数学概念、结论产生的过程,体验数学在解决实际问题中的价值和作用,形成积极向上的情感、态度和价值观[2].
江苏省苏州中学前身为苏州府学,为北宋政治家、文学家范仲淹创办.范仲淹在《上执政书》中说人才培养与选拔要“先策论以观其大要,次诗赋以观其全才.以大要定其留,以全才升其等级”,该法主张“明体达用”,实行“以类群居,相与讲习”,分“经义”“治事”二斋教学.经义斋研学经学基本理论,属“明体”之学;治事斋主攻农田、水利、军事、天文、历算等实学知识,属“达用”之学.据此我校卫新校长提出了基于核心素养的书院制育人模式,为了研究书院制育人模式的实践道路和贯彻苏州市教育系统落实拔尖创新人才培养要求,笔者以人教版数学必修第一册第162页“建立函数模型解决实际问题”这一课为例,进行探索研究如何有效培育学生“四基”.在此探索过程中笔者面向本校21级少预班学生开设了《函数中的“表”》的公开课.
2 教学过程
活动一
问题1:研究表明,40 ℃的温水比较适合人体饮用.那么在室温下,刚接好的一定温度开水大约需要放置多长时间才能适合人体饮用?
同学们,对于这个问题我们需要采集哪些数据,应该构建怎样的函数关系?
我们可以利用秒表、温度计等工具,收集水温随时间变化的数据.
学生每隔1 min测量一次水温,得到下表的一组数据.

时间/min012345678910水温/℃
设计意图:这样设计是为了提高学生兴趣,但由于需要合理分配时间,所以之后分两条线进行,请一位学生测量实验数据,其他同学进入知识回顾环节,等十分钟到了之后请学生报出测量数据.
活动二
问题2:观察下列函数表格中数据特点,写出可能的一个解析式.
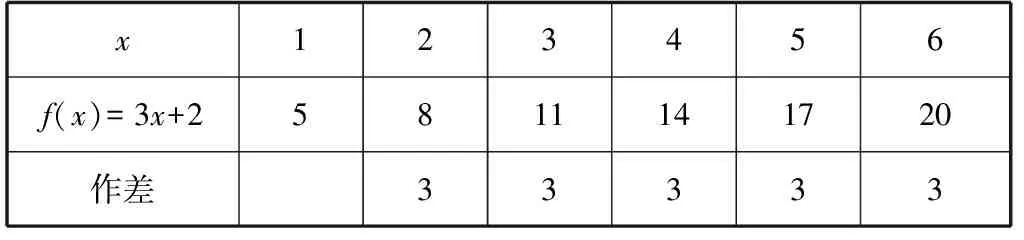
x123456f(x)=3x+25811141720作差33333
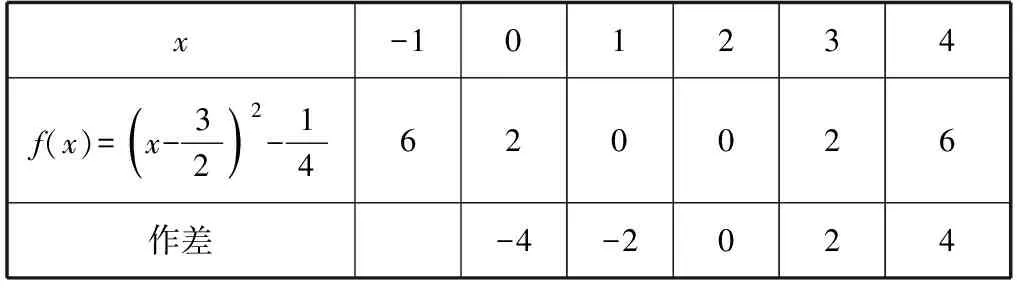
x-101234f(x)=x-32()2-14620026作差-4-2024
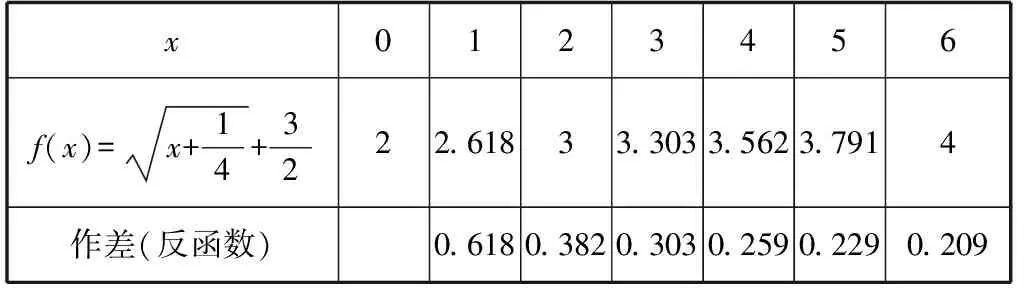
x0123456f(x)=x+14+3222.61833.3033.5623.7914作差(反函数)0.6180.3820.3030.2590.2290.209
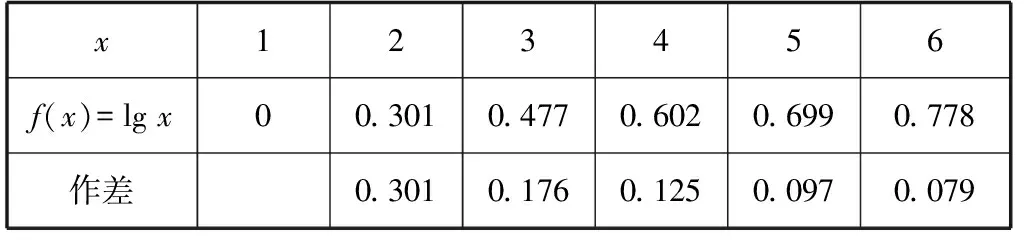
x123456f(x)=lg x00.3010.4770.6020.6990.778作差0.3010.1760.1250.0970.079
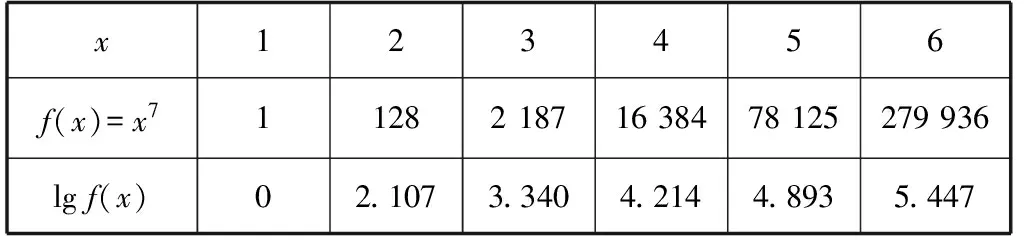
x123456f(x)=x711282 18716 38478 125279 936lg f(x)02.1073.3404.2144.8935.447
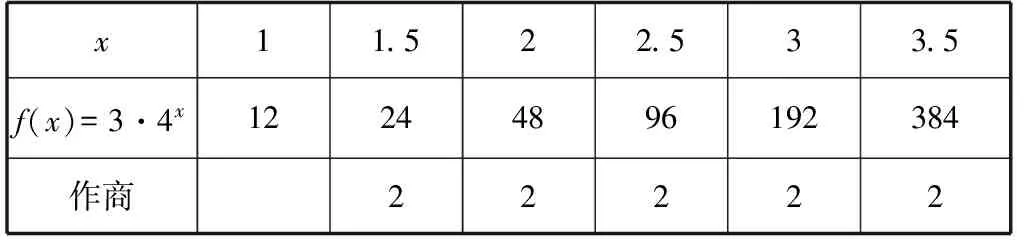
x11.522.533.5f(x)=3·4x12244896192384作商22222
小结:可以从函数的数据本身(作差、作商)或与其他函数间关系两方面来探究函数解析式.
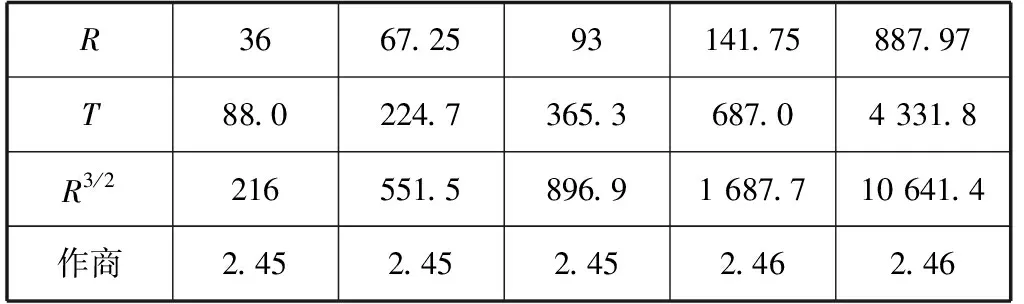
R3667.2593141.75887.97T88.0224.7365.3687.04 331.8R3/2216551.5896.91 687.710 641.4作商2.452.452.452.462.46
开普勒第三定律:以太阳为焦点的椭圆轨道运行的所有行星,其各自椭圆轨道半长轴的立方与周期的平方之比是定值.
设计意图:在天文历史中,科学家也遇到过从数据列表出发,寻找两个变量之间的规律,提出这样的列表问题使学生感觉这堂课的意义所在.
室温18.1 ℃

时间/min012345678910水温/℃9187.684.982.48077.675.573.671.769.867.9
设计意图:此时正好观察的同学已记录好实验数据,请他把数据一一报出.
活动三
问题3:如何分析水温与时间的数据,建立怎样的函数模型?
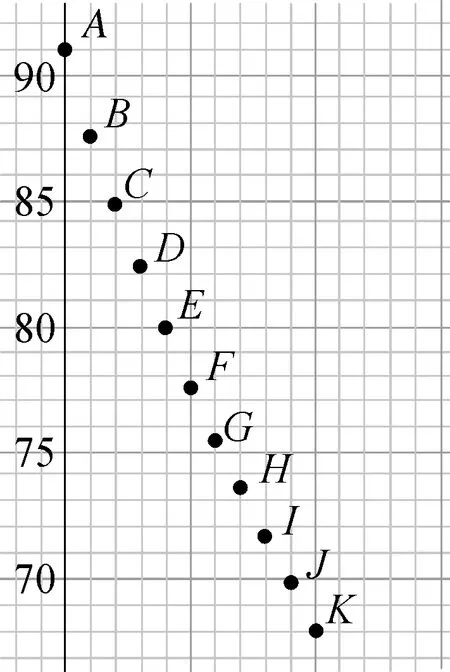
水温是时间的函数,但没有现成的函数模型.为此,可以先画出散点图,利用图象直观分析这组数据的变化规律,从而帮助我们选择函数类型.
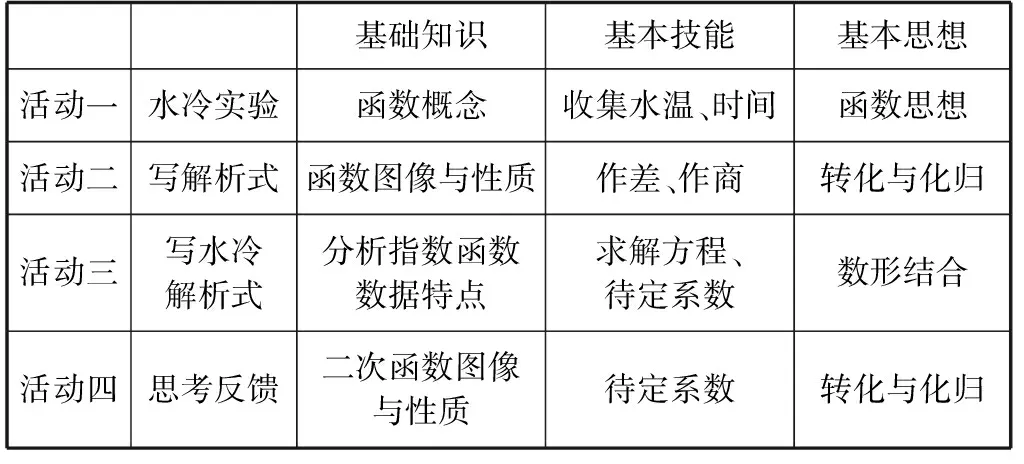
观察散点图的分布状况,利用前面数据分析有作差和作商的方法,并考虑到茶水温度降至室温(室温为t℃)就不能再降的事实,可选择函数y=kax+t(k∈R,0 为了求出温度的衰减比例a,可从第2 min的温度数据开始,计算每分(y-t(室温))的值与上一分(y-t(室温))值的比值,列出下表 x0123…nn+1…8910y-t…y1-ty2-t…比值…y2-ty1-t… 计算各比值的平均值,我们把这个平均值作为衰减比例,就得到一个函数模型 y=72.9·0.961x+18.1. 将已知数据代入函数解析式,并画出函数图形,检验函数模型与实际数据是否吻合,能否较好地反映水温随着时间的变化规律. 问题4:在室温下,刚接好的一定温度开水大约需要放置多长时间才能达到40 ℃,适合人体饮用? 活动四 问题5:经多次实验得到一辆汽车每小时耗油量Q(单位:L)与速度v(单位:km/h)(0≤v≤120)的下列数据: v406090100120Q5.268.3251015.6 为了描述汽车每小时耗油量(单位:L)与速度的关系,现有以下三种模型供选择: Q(v)=0.5v+a,Q(v)=av2+bv+c,Q(v)=av3+bv2+cv. 请填写表格空白处数据,并通过分析数据选出你认为最符合实际的函数模型,求出相应的函数解析式. 解:选择函数模型为Q(v)=av3+bv2+cv. 方法1: 方法2: v406080100120每小时∙∙∙耗油量Q(单位:L)5.261015.6百公里∙∙∙耗油量P(单位:L)131091013作差-3-113再作差2222 设计意图:这里表面上看为待定系数,其实可以根据前面的活动二通过二次函数两次作差为定值的特点得到顶点坐标,再代入一组数据得到二次项系数.使学生再次体会对于表中数据处理后运算较为简便. 课堂小结 (1)用数学的眼光看待世界(提出问题); (2)用数学的思维思考世界(建立模型); (3)用数学的语言表达世界(函数表示). “四基”指基础知识、基本技能、基本思想、基本活动经验.基础知识是指教材中的基本知识点,包括数学中的概念、性质、法则、公式、公理、定理;基本技能是指应用基础知识按照一定的程序与步骤进行解决问题;基本思想方法是指对数学理论与内容的本质知识,是从某些具体的数学内容和对数学认识过程中提炼上升的数学观点,它揭示了数学发展中普遍的规律,它直接支配着数学的实践活动,这是对数学规律的理性认识;基本活动经验是指经历思考、探究、实践等数学活动过程之后获得过程性知识、最终形成应用数学的意识.数学活动经验可以这样理解:数学活动经验是指学习者在参与数学活动的过程中所形成的感性知识、情绪体验和应用意识. 第一维度,基本数学知识的积累过程;第二维度,基本数学技能的演练过程;第三维度,基本数学思想方法的形成过程.这样一来,“四基”中前“三基”就已经形成了一个三维的“数学基础模块”.而基本数学活动经验本身并不构成一个单独的维度,而是填充在三维模块中间的粘合剂.事实上,数学教学是数学活动的教学.学生通过无处不在的基本数学活动获得的经验,与数学基本知识、基本能力、基本思想方法交织在一起,渗透在整体数学学习过程之中[3],如图所示,在具体上课过程中,设计了四个活动,活动一利用秒表、温度计等工具收集水温随时间变化的数据,使学生对水冷实验有初步的物理学上的经验认识;活动二观察给定函数表格中数据特点,写出可能的一个解析式,进而学生总结得出经验,可以从函数的数据本身(作差、作商)或与其他函数间关系两方面来探究函数解析式;活动三利用前面对于数据处理的基本经验和测量数据,探究水冷实验中时间和水温的函数关系式;活动四通过例题检验所学方法,使学生对于数据处理的基本方法经验进行再认知.这四个活动环环相扣,以基本活动经验为粘合剂,粘合基础知识、基本技能、基本思想. 基础知识基本技能基本思想活动一水冷实验函数概念收集水温、时间函数思想活动二写解析式函数图像与性质作差、作商转化与化归活动三写水冷解析式分析指数函数数据特点求解方程、待定系数数形结合活动四思考反馈二次函数图像与性质待定系数转化与化归 从表格中我们可以看出,本次公开课在基础知识、基本技能、基本思想中都动用了丰富的数学基础模块,使其形成了一个“四基”整体,其中的“实践”即为基本活动经验活动的途径,其中的“分析”即为在各个活动中提升数学基础模块的方法,从而通过“实践+分析”的方式有效培育学生的“四基”.
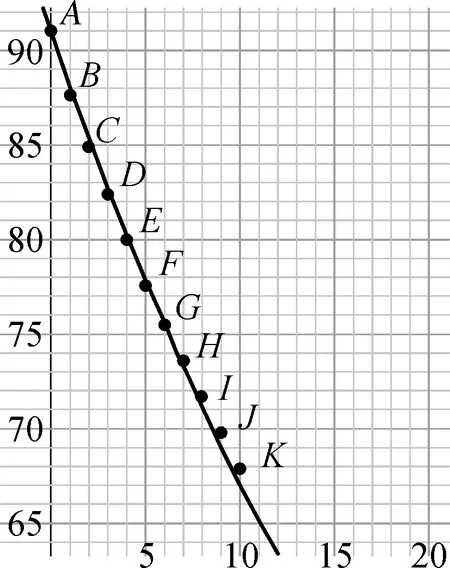


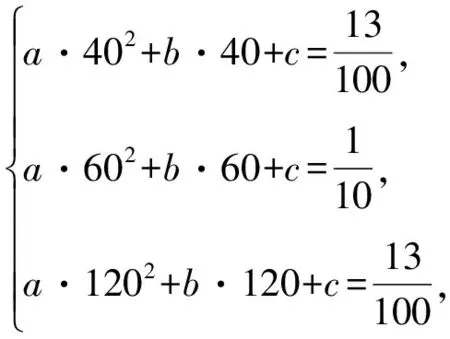
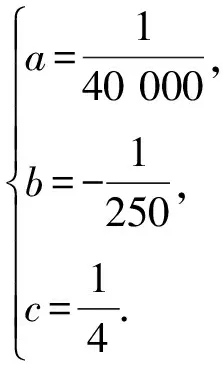

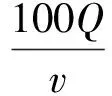
3 教学反思
3.1 在培育学生“四基”时,以基本活动经验粘合其余三维数学基础模块
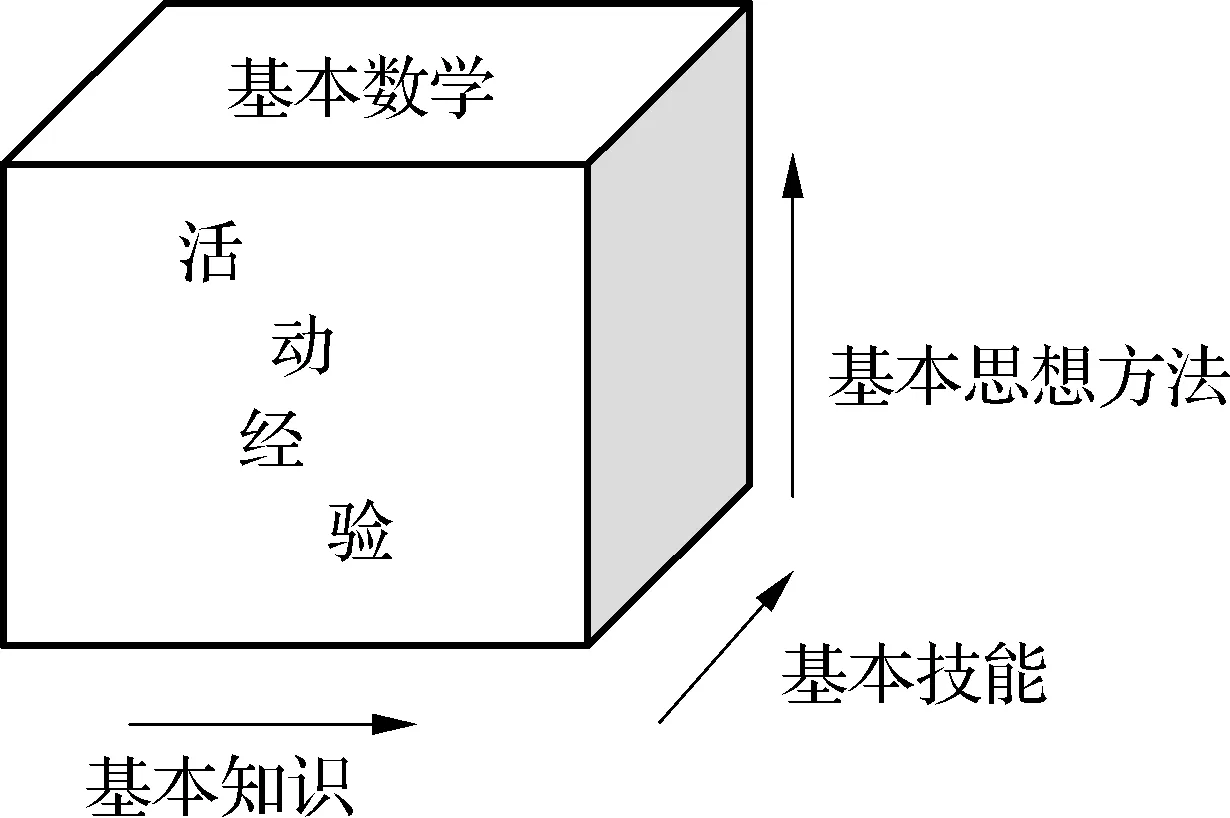
3.2 在培育学生“四基”时,三维数学基础模块相互渗透、相互交织