输电线⁃绝缘子体系三维抖振响应的时/频域理论方法研究

汪大海 王涛 汪伟 徐康 梁枢果

摘要：强风作用下往往产生大变形的非线性动力抖振响应，是导致电力网络风偏闪络和支撑杆塔风灾破坏的主要原因。为了揭示强风作用下输电线路风效应形成机理，以典型两跨输电线⁃绝缘子为研究对象，以绝缘子的风偏位移和杆塔对绝缘子端部的空间支座反力响应为考察重点，基于索结构力学，给出了静力平均风偏状态的非线性解，并考察了体系在风偏状态下模态、气动阻尼等动力特性的变化；推导了响应的影响线函数及模态参与系数表达式，提出了线性时域动力响应的计算方法；进而依据风工程理论，给出了脉动风振响应背景分量和共振分量的频域表达式；采用典型算例，通过与非线性有限元模型结果进行分析比较。结论表明，提出的三维振动时/频域理论模型及参数计算取值方法具备足够的工程效率和精度。研究为揭示输电线路风灾的破坏机理，完善输电线路结构的抗风设计提供了重要的理论基础和计算方法。

关键词：非线性；抖振响应；输电线；背景分量；共振分量

中图分类号： O322；TU312+.1    文献标志码： A    文章编号：1004-4523（2022）05-1109-09

DOI：10.16385/j .cnki .issn .1004-4523.2022.05.008

引言

高压输电线是典型的风荷载敏感结构，在各种风振响应中，强风作用下往往发生大变形的非线性动力抖振响应。这是导致电力网络风偏闪络和支撑杆塔风灾破坏的主要原因。国内外学者从理论分析计算、风洞试验和现场实测[1⁃7]等方面对大气边界层湍流作用下输电线的抖振响应及其传递给杆塔的风振荷载进行研究，研究结果也被当前的国际设计规范和标准所采用[8]。

输电线的风致响应可以分为静风荷载作用下的静力响应和静平衡状态处脉动风引起的动力响应。在较高的风速下，输电线平面的静力变形和风偏非常显著，这也使得输电线张力由初始状态（只受重力）发生了相当大的变化，从而导致了系统动力特性的变化。这就需要一个用于静态响应分析的非线性分析过程，而当张力变化可以被忽略时，线性理论更方便[9]。 Davenport[10]提出了基于传统线性随机振动理论的阵风响应因子方法。 Matheson 和 Holm ⁃es[11]通过使用有限差分法求解微分方程进行时域响应分析，与线性随机振动理论进行比较，还基于准定常理论计算了考虑气动阻尼效应的风致阻力。结果表明，输电线的平均风偏对输电线的竖向位移有明显的影响，也证实了横向支反力主要由背景分量贡献。文章通过不考虑风偏角的线性随机振动理论给出了较为准确的计算方法。Loredo ⁃ Souza 和 Daven ⁃port[12]比较了使用基于拟静力模型的线性随机振动理论和气弹风洞试验得出的响应，结果证实了由于气动阻尼较大，背景分量在横向响应中占主导地位。输电线的几何非线性风振响应可用非线性有限元模型计算，也可用关于模态位移的耦合非线性运动方程进行分析，其动力响应可以由平面内和平面外模态位移来表示。由于动张力的作用，模态位移方程与各非线性项耦合，其中包含基于变形协调条件的二次项[13]。事实上，当静力平衡状态附近的动力变形较小时，由动力响应引起的动张力可以通过系统线性方程来确定，线性系统可以使用随机振动的谱分析方法给出频域动力响应解[6]。

综上所述，目前的输电线风振响应的理论方法主要集中在单跨铰支输电线的顺风向振动方面。实际的输电线路由输电线与绝缘子连接而成。提出输电线路三维抖振响应的理论模型是揭示输电线路风灾破坏机理的关键。本文基于索结构力学和风工程理论，以典型两跨输电线⁃绝缘子体系的绝缘子风偏位移以及端部对杆塔的空间支座反力响应为研究内容，推导并建立了体系强风抖振空间响应的时/频域的理论计算方法。首先，推导给出了静力平均风偏刚度和变形的非线性解，并考察了其对体系模态、气动阻尼等动力特性的影响。进而在平均风偏状态下，分别推导了两种响应的影响线函数及模态参与系数，得到了时域线性动力响应理论计算方法，在此基础上，给出了脉动风振响应背景分量和共振分量的频域计算方法。最终，通过算例与非线性有限元模型结果分析进行比较，验证了该理论方法的精确性和效率。研究为完善和修订输电线路的抗风设计提供了理论基础。

1 静风响应分析

考虑两端固定在同一水平高度上的双跨输电线，中间通过长度为 l 的悬垂绝缘子与支座连接，垂跨比为 d0/L （d0为初始弧度）。初始状态下，单位长度重力荷载为 mg=q0，水平张力为 H0，初始位置为 y0（x），垂度为 d0=q0L2/（8H0），如图1（ a ）所示。不考虑输电线的抗弯刚度、输电线只承受拉力、输电线横截面积处处相等。本研究考虑风致响应最为不利的风向，即与输电线垂直的方向。绝缘子风偏状态示意图如图1（b）所示。单位长度上的平均风荷载由下式给出：

式中ρ为空气的密度；为水平支撑以下 d0高度处的平均风速，其值看作沿输电线跨度不变；CD 为阻力系数；D 为输电线直径。

带绝缘子输电线的微分方程与铰支座单跨输电线的静力平衡方程相似。易求得静风荷载作用下输电线的竖向和横向的静风位移0（ x ），0（ x ）分别为（其中，-L≤x≤L ）：

式中  0（0）= l （1- q0/q ），0（0）= D /q，分别为绝缘子端部竖向和横向静风位移，q =[ q 0（2）+fˉD2]0.5为风荷载与自重的合力，l 为绝缘子长度，L 为输电线跨度。水平张力 H 由下面的非线性方程确定：

式中  E 为杨氏模量，A 為输电线的横截面积。新平衡状态的 y（ x ）仍为抛物线，其弧垂为 d=qL2/（8H），输电线平面的风偏角为θˉ= arctan （ fˉD /q0），绝缘子上端三个方向的反力分量为：

2 背景分量计算

背景分量可以直接由影响线函数确定。对于 t 时刻一个给定的脉动响应（ t ），其背景分量 B 由下式给出：

式中μ（ x ）为影响线函数，表示当单位荷载作用在 x 处时引起 B 响应的增量。对于纵向脉动反力，其影响线函数可表示为：

其中，Irvine 常数λ2=（qL/H）2L/[HLe /（EA）]；输电线弧长 Le =L [1+8（d/L ）2]≈L 。对应于横向脉动反力的影响线函数为：

由于水平荷载作用在输电线上不会引起支座处的竖向反力，因此，对于竖向反力的影响线函数纵向位移μu 或者横向位移μw 的影响线函数可根据该方向的位移与反力的相似关系得到，可统一表示为：

依据公式（8）不难发现，由于横向分力 T͂z0（ t ）的影响线函数由平衡方程即可确定，因此，T͂z0（ t ）的背景分量不受风偏状态的影响。但是，绝缘子端部位移和纵向反力的影响线函数是水平张力 H 的函数，与风偏状态下的刚度有关。

依据线性随机振动理论，脉动风荷载作用下，背景分量的均方值可以计算为：

式中  IV =σV / V 为湍流强度，σV 和 S V （ f）分别为湍流的均方根和功率谱密度，f为频率，coh （ x 1，x2，f ）为脉动风相干函数。可以证明，直接使用影响线函数计算的背景分量与考虑所有背景模态的响应是等价的，因此影响线函数比模态分析方法效率更高，精度更好[6]。

3 共振分量计算

3.1  模态位移响应

共振分量通过模态分析确定。当静力平衡状态附近的动力变形较小时，动力响应引起的动反力与静反力相比也很小，动力方程可以基于准定常理论线性化，平面内和平面外模态位移的气动阻尼耦合动力方程表示为[6]：

式中qiv （t）和qiw （t）分别表示面内和面外的模态位移；ξiv 和ξiw为结构模态阻尼比；固有频率ωiv =2πfiv，ωiw =2πfiw，且fiv，fiw为输电线自振频率；Nv 和Nw分别为面内和面外模态截断数。气动阻尼比ξais1 和ξaijs1 s2（ s1= v，w；s2= v，w ）分别为：

其中，v 表示面内，w 表示面外，则有：

面内及面外模态的广义力可分别表示为：

式中fD （ x，t）=ρDCD  V （ x，t ）为脉动风荷载，V（x，t）是横向脉动风速。φiv （ x ）和φiw （ x ）分别为平面内和平面外的振型。依据线性振动模态叠加理论，时域内，系统的任意响应均可采用模态位移和对应的模态参与系数ri （ x ）表示为：

特别地，当所求 （ x，t ）为位移响应时，ri （ x ）即为模态φi （ x ）。

3.2  模态参与系数

模态参与系数可定义为模态惯性力下的静态响应。引入响应的影响线函数有：

式中μv （ x ），μw （ x ）为对应于该响应的面内及面外作用力影响线函数。考虑连续索结构的动力特征方程：

式中ΔHi 为水平附加张力。将公式（19）和（20）代入公式（17）和（18），可以得到：

对于本文重点考察的绝缘子端部支座处的反力响应，面内外反力T͂y和T͂z由模态位移和模态参与系数计算得到，而支座处纵向反力T͂x可根据位移和反力的比例关系求出，如下所示：

表示x =0处 t 时刻的面外位移，动反力在 x0，y0，z0方向的分力为：

面内外反力T͂y，T͂z亦可以根据纵向张力定

3.3  模态共振分量的频域计算

基于随机振动理论，对于非耦合模态振动，共振模态位移的均方根为：

其中，广义力的功率谱密度为：

则有ϑ vv = sin2θˉ，ϑ ww = cos2θˉ。一旦确定了模态位移的均方根，可以由 SRSS 方法（总响应为背景分量与共振分量之和）计算（ t ）的共振分量的均方根。响应的极值为静力响应加上峰值因子乘以响应的均方根[14]。依据现有研究，模态响应的背景分量与共振分量之间的相关性可以忽略不计[15].不难发现，由于风偏状态下输电线的频率和气动阻尼比发生了变化，共振分量也受到了静力风偏的影响。

4 算例分析

4.1  风场特性

考虑一根500 kV 的双跨输电线，它的参数如下：跨度 L=400 m，垂跨比 d0/L=1/30，线密度 m =2.39 kg/m，直径 D=0.036 m，EA=48.8 MPa 。初始张力 H0=35.2 kN，Irvine 常数λ2=98.6。输电线受到垂直于输电线平面的风荷载作用，阻力系数CD =1.0。风速曲线为 =0（ z/10）（1/6.5），0为10 m高度处平均风速，z 是地面以上高度，横向脉动风的功率谱密度由Kaimal谱给出：

式中  u*为摩擦速度，σ V = u*。在参考高度即支撑水平以下的 d0处，z=70− d0=61 m 。

脉动风的相干函数由 Davenport 的指数函数模型给 c（出）：

衰减因子为 C=16。除了上述模型之外，考虑到输电线的几何非线性，响应分析使用非线性有限元方法。

4.2  静风响应算例分析

图2显示了有限元和理论分析方法在不同风速下的垂度比 d/d0，水平张力比 H/H0，支座处反力比 y0/H0，面内外跨中位移比 w/d0和 v/d0，風偏角θ，结果表明，两种分析方法中的静力特性非常接近，验证了静风响应分析理论的正确性。从位移比和风速之间的斜率可以看出，由于几何非线性的影响，输电线的刚度随着风速的增大而增大。风速较大时，静张力随着静风荷载的增大而明显增大。

只有当两个振动模态频率彼此非常接近时，平面内和平面外模态响应的耦合效应才很重要。事实上，反对称的平面内和平面外的振动具有相同的模态频率和形状。一些对称的平面内模态的频率也可能非常接近具有对称的平面外模态的频率，需要考虑这些模态的耦合以及耦合气动阻尼项的影响。双跨输电线⁃绝缘子体系的前几阶模态的示意图如图图3所示，考虑到悬垂绝缘子轴向拉伸刚度较大，可忽略其轴向受拉变形，仅需考虑绝缘子对于面外对称模态的影响。未耦合的模态响应可以看成单自由度系统进行计算。

4.3  动力响应

采用谱表现方法，可以方便地模拟多个位置的平稳脉动风[16]。截止频率fmax =5 Hz，频率增量Δf=5/4096 Hz=0.0012 Hz 。脉动风持续时间为500 s，时间间隔为Δ t=0.125 s 。参考高度处的平均风速为 =30 m/s，湍流强度取为 IV =11%。

对于给定的脉动风时程样本，采用有限元和模态分析方法计算风振响应时程。在模态分析方法中，包括在面内和面外方向上的前12阶模态，即总共24阶模态。基于耦合运动方程的 Newmark 方法确定模态分析响应，包括背景分量和共振分量。与气动阻尼相比，结构模态阻尼很低，故可以忽略结构模态阻尼。首先消除了前100 s响应时程，即消除了

瞬态结构动力的影响。通过模态分析与非线性有限元分析结果进行了比较。图 4和5分别给出了支座处位移时程和功率谱。图 6和7给出了支座动反力响应时程及其功率谱。

除了进行以上模态响应时程分析外，下文还采用非线性有限元方法进行响应分析，并与响应谱理论分析模型的结果进行了比较。为了研究静力平衡对动力响应的影响，基于理论公式的响应谱分析，其中背景分量使用影响线函数计算，共振分量通过模态分析确定，将是否考虑输电线静力风偏角的两种计算结果与有限元方法比较。图 8显示了位移和反力分量的均方根随风速的增加而增大，湍流强度 IV =11%。

可以发现，考虑输电线平面静力风偏的响应与非线性有限元分析结果吻合较好。由于气动阻尼较大，动力响应主要来源于背景分量。如前所述，横向动反力的背景分量不受输电线平面静力风偏的影响。然而如图8（ a ）所示，当不考虑输电线平面静力风偏时，在支座处横向位移的背景分量和总响应显然被高估了。另外如图8（b）和（d）所示，不考虑静力风偏无法准确计算竖向位移和纵向反力分量。

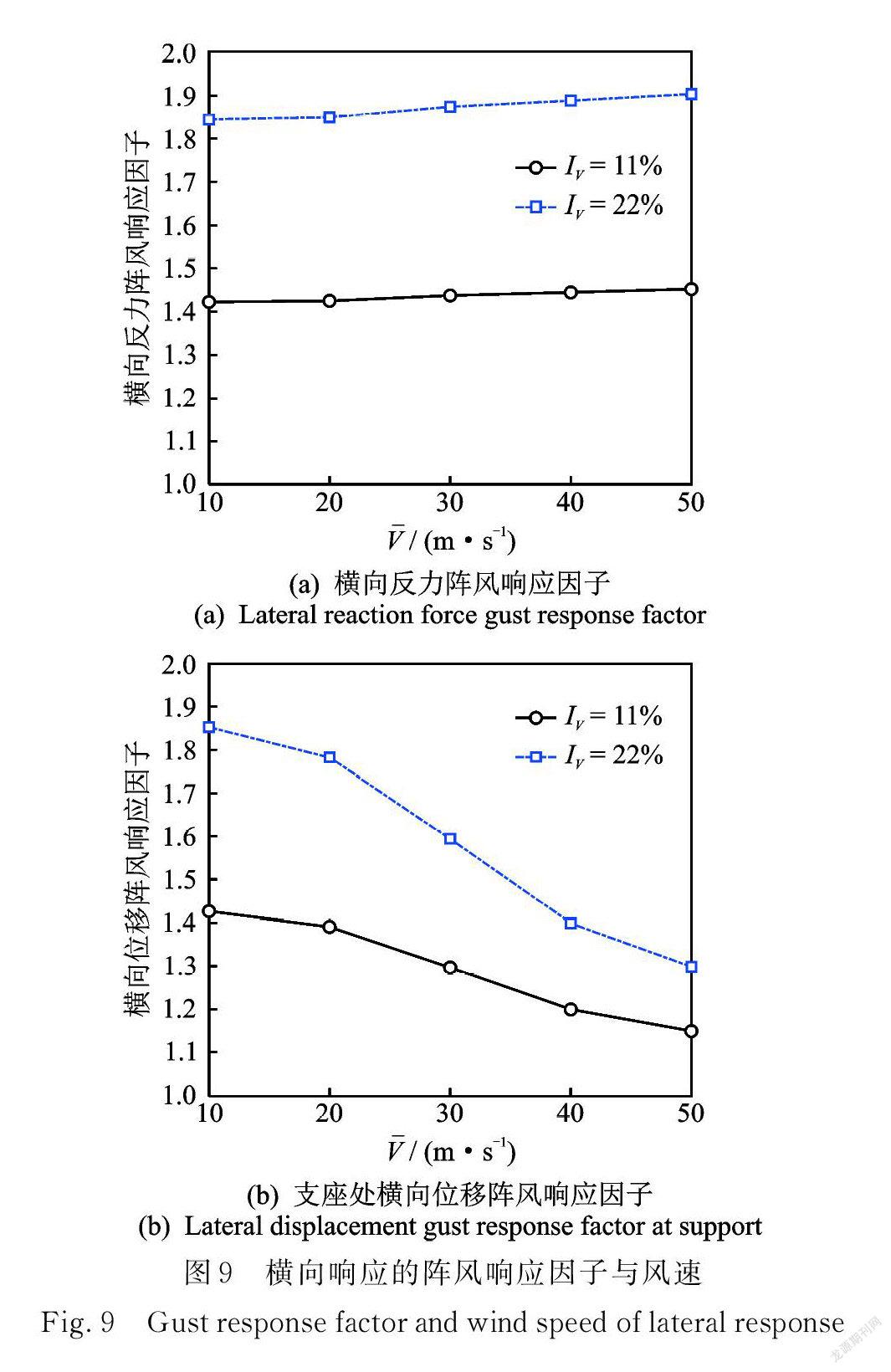
对于上述响应，峰值因子范围为2.68到4.03。如图9所示，当 IV =11%时，随着风速的增加，横向动反力的阵风响应因子 GRF（Gust Response Fac⁃ tor）从1.42略微增加到1.45。而横向位移的 GRF 从1.42减小到1.15。由于脉动响应与湍流强度成正比，因此湍流强度越高，GRF 越大。

5 结论

本文以典型两跨输电线⁃绝缘子体系的绝缘子风偏位移以及端部对杆塔的空间支座反力响应为研究内容，将风效应分为平均风作用下的几何非线性静力效应和脉动风作用下的线性动力效应，基于悬索力学理论，通过推导体系的影响线函数和模态参与系数，分别计算了背景分量和共振分量。逐步建立了体系强风抖振空间响应的时/频域的理论计算方法。具体结论如下：

（1）平均风荷载导致了几何非线性的静风响应，输电线平面发生了风偏，水平风荷载还引起了平面内和平面外模态振动响应。与此同时，输电线弦向张力也有了显著提高，改变了系统的自振频率和气动阻尼等动力特性。

（2）利用影响线函数可方便高效地計算脉动风荷载的背景分量，且可以得出模态参与系数，用以计算共振分量。除了横向支反力响应外，其他响应的影响线函数均会受到静力风偏状态的影响。由于较高的气动阻尼，脉动响应以背景分量为主要贡献，共振分量以一阶振动为主。

（3）不考虑输电线静力风偏将显著高估绝缘子横向位移的背景分量及脉动响应，同时也无法计算竖向位移、纵向反力和竖向动反力分量。因此在动力响应分析中考虑静力非线性变形对脉动风动力响应的影响是十分必要的。

（4）通过与非线性有限元分析比较，本文提出的三维振动理论模型具备足够的工程效率和精度。

参考文献：

[1] 邓洪洲，朱松晔，陈晓明，等.大跨越输电塔线体系气弹模型风洞试验[ J ].同济大学学报（自然科学版），2003，31（2）：132-137.

Deng  Hongzhou，Zhu  Songye，Chen  Xiaoming，et  al . Wind tunnel investigation on model of long span trans⁃ mission  line  system [ J ]. Journal  of  Tongji  University （Natural Science），2003，31（2）：132-137.

[2] 梁枢果，邹良浩，韩银全，等.输电塔-线体系完全气弹模型风洞试验研究[ J ].土木工程学报，2010，43（5）：70-78.

Liang  Shuguo， Zou  Lianghao， Han  Yinquan， et  al . Study of wind tunnel tests of a full aero-elastic model of electrical  transmission  tower-line  systems [ J ]. China Civil Engineering Journal，2010，43（5）：70-78.

[3] 谢强，严承涌.1000 kV 特高压交流同塔双回输电塔线耦联体系风洞试验[ J ].高电压技术，2010，36（4）：900-906.

XieQiang，Yan Chengyong . Wind tunnel test on 1000 kV UHV AC double circuit transmission tower conduc ⁃ tor  coupling  system [ J ]. High  Voltage  Engineering，2010，36（4）：900-906.

[4] 楼文娟，孙珍茂，许福友，等.输电导线扰流防舞器气动力特性风洞试验研究[ J ].浙江大学学报（工学版），2011，45（1）：93-98.

Lou Wenjuan，Sun Zhenmao，Xu Fuyou，et al . Experi⁃ mental study  on  aerodynamic characteristics of air flow spoiler[ J ]. Journal of Zhejiang University （Engineering Science），2011，45（1）：93-98.

[5] 李正良，任坤，肖正直，等.特高压输电塔线体系气弹模型设计与风洞试验[ J ].空气动力学学报，2011，29（1）：102-113.

Li Zhengliang，Ren  Kun，Xiao Zhengzhi，et  al . Aero ⁃ elastic  model  design  and  wind  tunnel  tests  of  UHVtransmission  line  system[ J ]. Acta  Aerodynamica  Sini⁃ ca，2011，29（1）：102-113.

[6]  Wang  Dahai， Chen  Xinzhong， Li  Jie . Prediction  ofwind-induced buffeting response of overhead conductor：comparison  of linear  and  nonlinear  analysis  approaches [ J ]. Journal of Wind Engineering and Industrial Aerody⁃ namics，2017，167：23-40.

[7]  Momomura Y，Marukawa H . Full-scale measurementsof wind-induced vibration of a transmission line system in a mountainous area[ J ]. Journal of Wind Engineering and Industrial Aerodynamics，1997，72：241-252.

[8]  Task Committee on Structural Loadings of the Commit⁃tee  on  Electrical Transmission  Structures  of the  Struc ⁃ tural  Engineering  Institute  of the  American  Society  of Civil Engineers . Guidelines  for Electrical Transmission Line Structural Loading[M]. USA：American Society of Civil Engineers，2010.

[9]  Pasca  M ，Vestroni  F ，Gattulli  V . Active  longitudinalcontrol of wind-induced oscillations of a suspended cable [ J ]. Meccanica，1998，33（3）：255-266.

[10] Davenport A  G . Gust response factors for transmissionline loading[ J ]. Wind Engineering，1980，2：899-909.

[11] Matheson，M J，Holmes J D . Simulation of the dynamic response of conductor in strong winds[ J ]. Engineer? ing Structures，1981，3（2）：105-110.

[12] Loredo-Souza A M，Davenport A G . Wind tunnel aero ⁃elastic  studies  on  the  behaviour  of  two  parallel  cables [ J ]. Journal of Wind Engineering & Industrial Aerody⁃ namics，2002，90（4）：407-414.

[13] Di Paola M，Muscolino G，Sofi A . Monte Carlo simula ⁃tion for the response analysis of long-span suspended ca⁃ bles under wind loads[ J ]. Wind & Structures，2004，7（2）：107-130.

[14] Davenport A  G . Note on the distribution of the largestvalue  of  a  random  function  with  applications  to  gust loading[ J ]. Proceedings of the Institution of Civil Engi⁃ neers，1964，28（2）：187-196.

[15] Chen  X ， Kareem  A . Evaluation  of  equivalent  staticwind loads on buildings[C]. Proceedings of 10th Ameri⁃ cas  Conference  on  Wind  Engineering ，Baton  Rouge， LA，USA，2005.

[16] Peng L，Huang G，Kareem A，et al . An efficient space-time  based  simulation  approach  of  wind  velocity  field with  embedded  conditional  interpolation  for  unevenly spaced locations[ J ]. Probabilistic Engineering Mechan⁃ ics，2016，43：156-168.

Frequency and time domain analytical methods for wind -induced buffeting response of overhead conductor

WANG Da-hai1，WANG Tao1，WANG Wei2，XU Kang3，LIANG Shu-guo4

（1.Department of Architectural Engineering，School of Civil Engineering and Architecture，Wuhan University of Technology，Wuhan 430070，China；2.Guangdong Electric Power Design Institute，Guangzhou 510799，China；3.State Grid Electric Power Research Institute Wuhan Nari Group Corporation，Wuhan 430072，China；4.School of Civil Engineering，Wuhan University，Wuhan 430070，China）

Abstract： The nonlinear dynamic buffeting response with large deformation often occurs under the action of strong wind，which will always lead to wind flashover of power network and the wind damage of supporting towers . In order to reveal the formation mechanism of wind effect on transmission lines under the action of strong wind，this paper takes the typical two-span transmission lines-insulators as the research object，and studies on the wind deflection displacement of insulators and the reaction response of towers to the spatial supports at the end of insulators . Based on the cable structure mechanics，the nonlinear solution of the static average wind deviation state is analyzed，and the changes of dynamic characteristics such as mode and aerodynamic damping of the system under wind deviation are investigated . The expressions of the influence line function and modal participation coefficient of the response are derived，and the calculation method of linear dynamic response in time domain is proposed . According to the theo⁃ ry of wind engineering，the frequency domain expressions of background component and resonance component of fluctuating wind vibration response are given . A typical example is used to analyze and compare with the results of nonlinear finite element model . The results show that the three-dimensional vibration time/frequency domain theoretical model and the parameter calculation meth ? od proposed in this paper have sufficient engineering efficiency and accuracy . The study provides a theoretical basis and calculation method for revealing the damage mechanism of transmission line wind disaster and improving the wind-resistant design of transmis⁃ sion line structure .

Key words ： nonlinear；buffeting response；transmission line；background component；resonant component

作者简介：汪大海（1975—），男，博士，教授。电话：13657236629；E-mail：wangdahai@whut .edu .cn。