多子群多策略差分进化算法

高媛，姜志侠，刘宇宁

（1.长春理工大学 数学与统计学院，长春 130022；2.中电金信软件有限公司，北京 100192）

差分进化算法（Differential Evolution，DE）是由Storn等人在1995年为解决Chebyshev多项式问题所提出的，现在已经成为解决复杂优化问题的常用方法［1-2］。DE算法是一种结构简单、鲁棒性强的全局搜索算法，在物流调度［3］、运动目标检测［4］、成本控制［5］、数据挖掘［6］等许多领域得到了广泛的应用。

差分进化算法主要由变异、交叉、选择和边界条件处理几步组成。经过几十年的发展，众多基于标准DE算法的改进算法被提出。Brest J［7］为每个个体设置了可以自动调整的控制参数，提出了jDE算法。Qin等人［8］运用个体之间的迭代经验来自适应调整参数和变异策略，提出了自适应差分进化算法（SaDE），提高了算法的收敛速度。为了完善差分进化算法在解决高维优化问题时存在的缺陷，张锦华等人［9］结合了DE-rand-1和DE-best-1的优点，并将其加权组合，提出了WMDDE算法。陈颖洁等人［10］提出了一种以优秀个体为导向的多策略差分算法，该算法将种群等分为三个子种群，根据每个部分不同的特点，采取了不同的变异策略。

本文首先将种群按照适应度值从小到大排列，并将其按一定比例分为三个子种群，针对每个子种群不同的搜索能力构建不同的变异策略，设置不同的控制参数。针对第一个适应度值较好的子种群，使用DE-best-2变异策略，提高种群收敛速度和搜索能力。针对第二个适应度值中等的子种群提出了一种基于优秀个体的DE-rand-1 to DE-best-1变异策略，这有利于平衡种群的全局搜索和局部搜索能力。针对第三个适应度值较差的子种群提出了一种引入学习参数和均衡参数的组合变异策略，以此降低种群陷入停滞状态的概率，保持算法的稳定性。

1 标准DE算法

DE算法作为一种进化类算法，结构中包含了变异、交叉、选择三种进化操作。设DE算法的第t代种群由NP个维数为D的实数值参数向量组成，第i个个体表示为：xi(t)(i=1,2,…,NP)。

1.1 变异操作

标准DE算法采用差分策略产生变异向量。对于每个目标向量xi(t)(i=1,2,…,NP)，常用的变异策略如下：

1.2 交叉操作

交叉操作的目的在于提高种群的多样性。标准DE算法的交叉操作如下：

其中，j=1,2,…,D；jrand为[1 ,2,…,D]之间的随机数，来确保交叉个体至少有一个分量会与目标个体不同；CR称为交叉算子，取值一般为[0 ,1]内的实数。

1.3 选择操作

选择操作在目标个体及交叉个体之间进行，通过优胜劣汰的竞争法则，选取其中更加适应环境的个体进入子代继续繁衍，使种群向最优解的方向进化。其迭代公式如下：

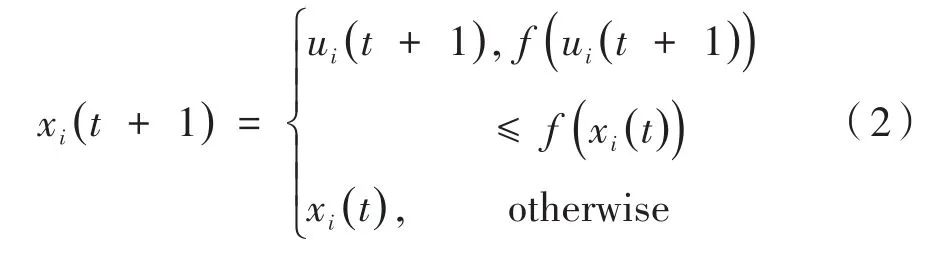
2 多子群多策略DE算法

下面提出一种多子群多策略DE算法，记为“改进DE”算法。

2.1 初始化种群

根据问题需要，确定种群个数NP及个体维数D，按下式随机生成的初始种群(t=0)：

其中，xmax(t)，xmin(t)表示取值区间的最大值和最小值；rand(0 ,1)是在区间[0 ,1]上的随机数。

设计“改进DE”算法的关键问题是如何划分种群、选择变异策略和设置参数。“改进DE”算法针对每个子种群不同的搜索能力构建不同的变异策略、设置不同的控制参数，使得各子种群具备不同的搜索能力，体现不同的作用，保持整个种群的搜索和开采能力。本文根据适应度值从小到大的排序将种群分为三个子种群，选取前10%个体作为第一个子种群即优秀种群，第二、第三个子种群根据经验分别选择40%和50%。

2.2 第一个子种群X1（优秀种群）

针对第一个子种群X1（优秀种群），考虑到个体适应度值较好，为了提高种群的收敛速度并且增加种群的搜索能力，不使种群陷入停滞的状态，同时也能够维持整个种群的平衡状态，采用了开采能力较强的DE-best-2变异策略：

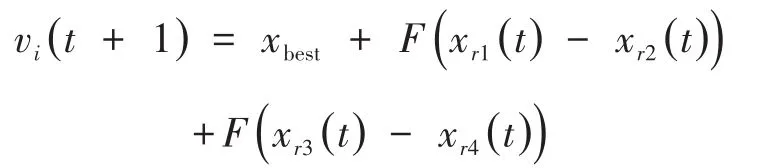
其中，xbest为种群当前的最优个体；xr1(t)，xr2(t)，xr3(t)，xr4(t)为子种群X1中随机选取的四个不同个体。该策略具有较强的局部寻优能力，可以在子种群X1中选择更接近最优解的解。在第一个子种群中F设为0.9可增加差分向量的扰动程度，有利于增强算法的搜索能力，CR设为0.1，是因为第一个子群X1本身就为优秀种群。考虑到交叉算子CR可以控制种群中试验个体的多样性，较大的CR值使得试验个体更多地继承变异个体的性质，这样可以使种群增强搜索能力；相反，变异算子CR值越小，试验向量改变越小，有助于种群保持多样性。

2.3 第二个子种群X2

DE-best-1因包含全局最优个体，局部寻优能力突出，适合求解单峰类型的问题；而DE-rand-1包含的个体均为随机选择，使得该策略的全局搜索能力突出，适合求解多峰类型的问题。因此对于适应度值中等的子种群X2来说，参考文献［10］引入学习参数μ(xi(t))构造一种新的加权变异策略，用来平衡子种群X2的全局搜索能力和局部开发能力。

学习参数定义如下：

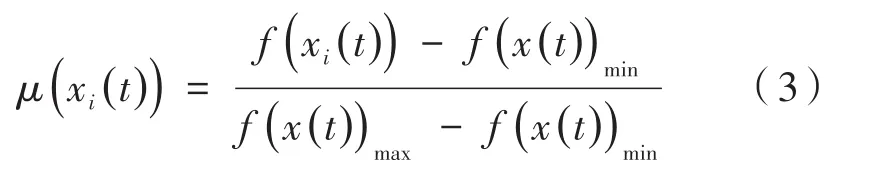
其中，t是当前迭代次数；f(xi(t))为个体xi(t)的适应度函数值；f(x(t))min和f(x(t))max表示种群在当前代数t中个体适应度值的最大值和最小值。μ(xi(t))为单调递增函数，随着适应度函数值f(xi(t))的增大而增大。设种群规模NP=100，维数D=50，F=0.6，CR=0.9，以函数f1为例，其中f1的表达式为：

图1更加直观地展示出函数f1的学习参数μ(xi(t))在第一次迭代中的变化曲线。

图1 种群X2中 μ(x i(t))的变化曲线

定义引入学习参数的加权变异策略DE-rand-1 to DE-best-1：

其中，xr1，xr2，xr3，xr4，xr5为X2中随机选取的不同个体；μ(xi(t))为单调递增函数，随着适应度函数值f(xi(t))的增大而增大。

可知构造的变异策略在前期，主要进行全局搜索，随着μ(xi(t))的递增，后期主要以在xbest附近进行局部开发，其中rand(0 ,1)用来随机调整算法的进化方向，引导个体朝着最优值靠近，从而提高种群多样性，避免DE算法停滞和过早收敛的情况。

2.4 第三个子种群X3

在变异策略中，种群的多样性在很大程度上与所选取的搜索中心有关，也就是围绕着哪个个体进行差分进化，称这个个体为基向量。设当前迭代次数为t，对个体xi(t)参考文献［10］定义均衡参数EP(xi(t))和系数at：

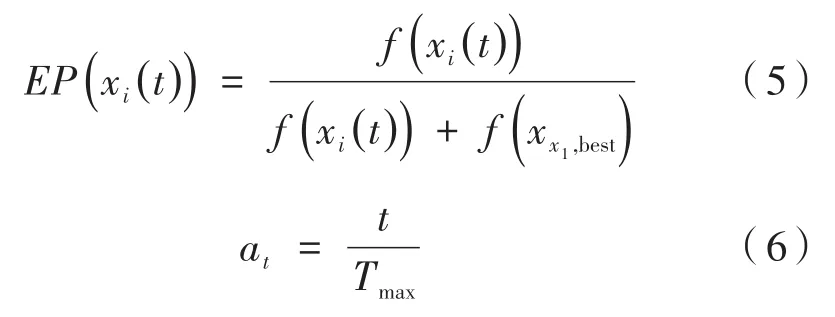
其中，xx1,best是在优秀种群中随机选取的个体，Tmax是最大迭代次数，随着进化的推进，由式（6）可以看出系数at的值是在逐渐增大。

μ(xi(t))，EP(xi(t))，1-EP(xi(t))为f(xi(t))的单调函数，即当个体适应度值越大时，μ(xi(t))和EP(xi(t))的值越大，而相应1-EP(xi(t))的值越小。

对于子种群X3中的个体xi(t)，当其适应度值越大时，其向优秀种群中个体的学习能力就需越强，因此用学习参数μ(xi(t))来增强其向优秀个体的学习能力，引入呈递减趋势的均衡参数1-EP(xi(t))是为避免其收敛过快，陷入局部最优的状态。而1-μ(xi(t))的作用则是当其适应度值越小时，子种群X3中个体越需要降低其向优秀种群中个体的学习能力。为了避免子种群X3中个体因适应度值较差而向优秀种群学习能力过大的情况，引入呈递减趋势的均衡参数EP(xi(t))来对其自身进行平衡。

仍以函数f1为例，图2更加直观地展示出第三个子种群在第一次迭代中均衡参数EP(xi(t))随着个体的变化而上升的变化曲线。

图2 种群X3中EP(x i(t))的变化曲线

选取以下变异策略：

其中，xbest是当前迭代的全局最优值；xr1(t)，xr2(t)，xr3(t)是在子种群X3中随机选取的三个个体。这里randnormal是指以ui(t)为均值，0.1为方差的正态分布形成的个体。randnormal的目的为探索周围邻域存在的有潜力解，相比于文献［10］中的柯西分布，考虑到正态分布比柯西分布在峰值附近的取值概率更大，接近最优值的概率更多，因此引入正态分布保证了以较大的概率生成均值的控制参数值，同时不丢失随机性，保证了种群的多样性。实验结果表明正态分布在变异策略中可以起到较好的效果。对于变异策略中差分向量采取随机的机制，从而在基向量的基础上向周围寻优。对于适应度越差的子种群X3中的个体，为了避免整个种群陷入局部最优状态从而引入均衡参数，其目的在于当它向优秀的个体学习的学习参数较大时，减缓向优秀的个体学习的速度。当它向优秀个体学习参数较小时，变异向量个体侧重在个体自身与差分向量的组合基础上产生，因此CR取0.9有利于维持种群的多样性。

2.5 算法流程

通过对不同的子种群使用不同的变异策略和控制参数的选取，使得不同的变异策略和参数在种群的进化过程中所发挥的作用不同，使得各个种群之间的搜索能力能够互补，最终达到平衡全局搜索能力和局部搜索能力的作用。算法流程如图3所示。

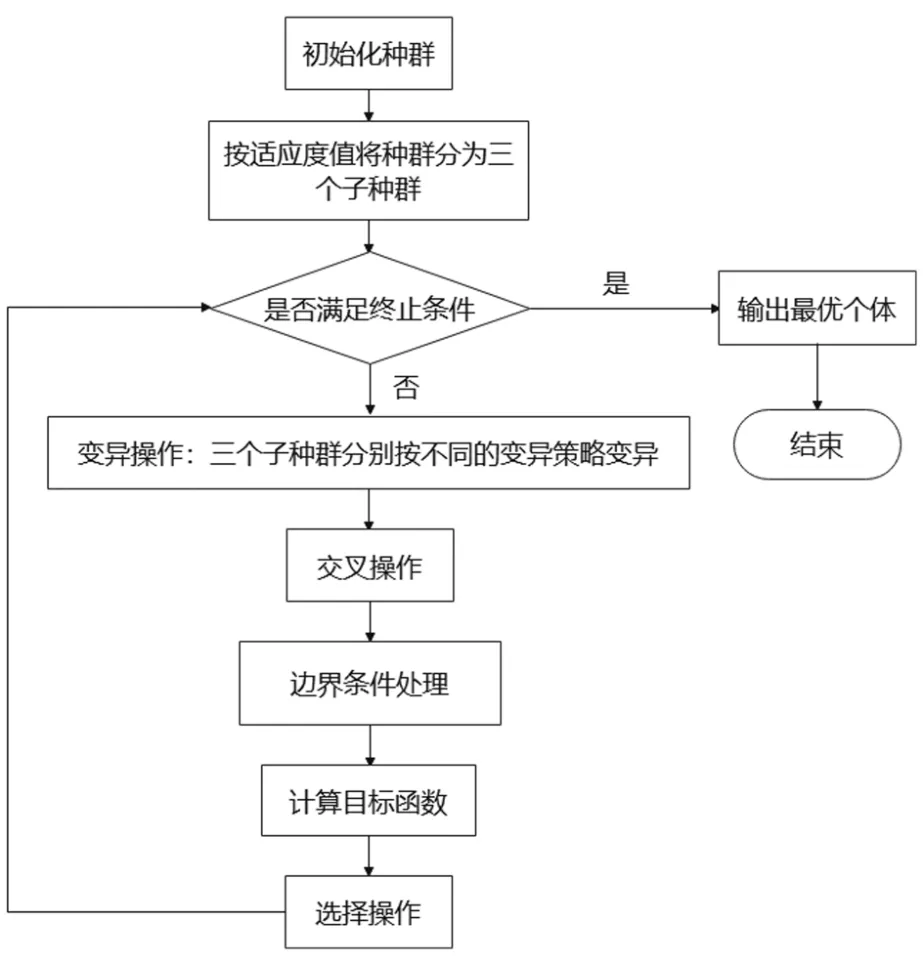
图3 算法流程图

3 数值实验

针对提出的“改进DE”算法，选取8个经典的测试函数对算法的性能进行测试，函数全局最优值均为0。8个测试函数表达式如表1所示。

表1 测试函数

用以上提到的常见的四种差分变异策略DE-best-1、DE-rand-1、DE-best-2、DE-current-tobest-2与“改进DE”算法计算8个测试函数的最优值，为了考察算法的综合性能，设置种群规模NP=100，维数D=50，所有算法最大迭代次数均为1 000次。结果对比如表2所示。

表2 测试函数最优值结果对比NP=100，D=50，Tmax=1000

五种算法对8个函数进行测试的适应度值的迭代曲线如图4所示，从图中可以看出本文所提出的“改进DE”算法在迭代过程中所展示的良好的性能，迭代曲线下降速度较快，并且寻优精度较高，相比于其他算法总体上寻优能力强，收敛速度快。

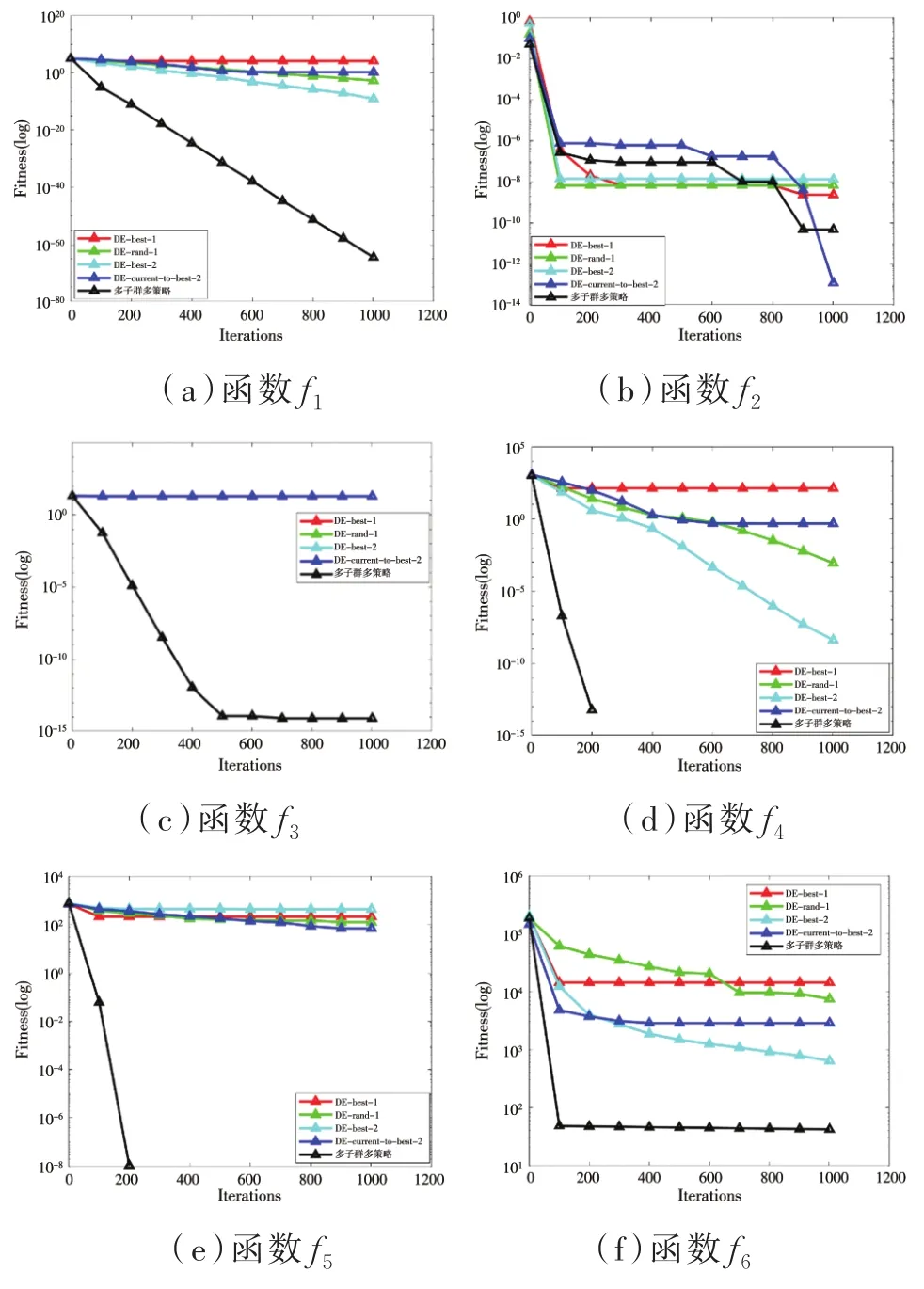
图4 测试函数迭代曲线

4 结论

本文在标准DE算法的基础上，将种群按适应度值从小到大排列并按一定比例分为三个子种群，针对不同子种群采用了不同的变异策略，进而使不同的变异策略在不同子种群进化过程中发挥不同的作用。

第一个子种群采用标准DE算法中DE-best-2变异策略，该策略具有较强的局部寻优能力。针对第二个适应度值中等的子种群引入学习参数，结合DE-rand-1和DE-best-1变异策略的各自优点，提出了一种新的变异策略DE-rand-1 to DE-best-1，该变异策略通过学习参数在全局搜索和局部搜索之间建立一种平衡。针对第三个适应度值较差的子种群提出了一种引入学习参数和均衡参数的组合变异策略，使其能够更加平衡的向优秀种群中的个体进行学习，以此降低种群陷入停滞状态的概率，保持算法的稳定性并达到更优的状态。通过8个测试函数的实验结果可得出，“改进DE”算法在大多数函数上的寻优能力和收敛速度上都有了一定的提升，并具有较强的稳定性。