基于计算鬼成像的层析成像研究
邵嘉琪,李畅,闫凌浩,刘娜,张烨
(长春理工大学 物理学院,长春 130022)
“鬼”成像(Ghost Imaging,GI),又称双光子成像或关联成像,是一种利用双光子符合探测恢复待测物体空间信息的一种新型成像技术。不同于传统光学成像的基于光场强度的分布测量,鬼成像是基于光场的强度涨落的关联测量,凭借抗噪声能力强、高分辨率、能突破衍射极限成像等优势,受到了广泛关注。鬼成像的实验方案最早是由前苏联学者Strekalov等人[1]根据自发参量下转换光子对的纠缠行为提出。1995年Pittman等人[2]正式提出了鬼成像的原型,宣告了鬼成像的诞生,同年Shih等人[3]利用纠缠光子对结合符合测量技术,实现了关联成像。2008年,Shapiro等人[4]提出了计算鬼成像的实验方案。次年,Bromberg等人[5]首次在实验上验证计算鬼成像,仅用一个光强探测器就实现了基于赝热光的计算鬼成像,进一步简化了成像系统。2011年,Hardy等人[6]研究发现在大气湍流干扰的情况下,计算鬼成像方案相比于传统鬼成像方案能够提高其成像质量。所以计算鬼成像相比于传统鬼成像,实验结构简单并且具有更大的实用价值[7-14]。
早期对于鬼成像的研究,所得到的物体的重构图像主要为待测物体的空间信息,而无法对客观世界中的三维物体进行还原,如今的三维成像除了可以获得物体的空间信息之外,还可以获取更多关于物体的维度信息。因此,三维鬼成像引起了很多学者的重视[15-20]。2009年,应关荣等人[21]提出了一种基于强度关联成像的新型三维衍射层析技术,利用关联成像并结合衍射层析技术和二步相位恢复算法实现了强度关联三维衍射层析。
2019年,Sun等人[22]利用单像素成像通过使用一系列掩膜图案对场景进行采样,并将这些掩膜图案中的信息与单像素探测器测量得到的相应光强做关联计算以重建图像。
本文提出了一种新的利用鬼成像技术恢复位于光源不同距离处的不同层面待测物体信息的理论模型,然后基于理论分析进行了数值仿真实验,成功恢复了多个层面待测物体的信息,从而验证了鬼成像技术可实现层析成像的可行性。
1 层析鬼成像技术理论模型
层析鬼成像的成像系统结构图如图1所示,选用两个平面(平面1、平面2)放置待测物体,平面1到光源的距离为Z1,平面1到平面2的距离为Z2。利用计算机控制投影仪将预先生成的一系列照明散斑图样投射到空间光调制器进行调制,经空间光调制器进行调制之后继续传播一定距离后投射到一系列物体上,光强最终被桶探测器接收。经过传播与收集之后,得到一系列的散斑图样和桶探测器信号。此时,可以通过将散斑图样与桶探测器上收集到的光强值进行二阶关联运算来对两个平面的待测物体进行清晰的成像。二阶关联函数如下:

图1 层析鬼成像系统结构图

其中,Ib是桶探测器收集到的总的光强值;Ia(x,y)是连接计算机的光源发射出的预设照明散斑图样照射到待测物体所处平面上所形成的光强分布;表示求统计平均值。由于二阶关联函数主要是由桶探测器接收到的光强值与照射到待测物体表面的散斑二者进行关联运算,如果照射到两个物体上的散斑图样的涨落一致,则无法恢复出两个层面的待测物体信息。所以物体的成像与Ia(x,y)平面的光强信息有关,当照明散斑图样传播一定距离后,通过计算不同平面上的Ia(x,y)值,则可以恢复出不同层面物体的图像信息。
照明散斑图样在自由传播过程中会发生变化。当照明散斑图样传播到距离光源不同位置处时,其散斑的光强涨落会有所不同,此时可以由此计算二阶关联函数中Ia(x,y)的值。图2为正态分布的随机散斑图样经过传递后的光强分布变化情况。

图2 正态分布的随机散斑传播不同距离Z后的光强变化情况
在该成像系统中,由可调控光源照射出散斑图样,将其记为E(x0),在空间中自由传播距离Z1后到达平面1上的物体1,将物体1光平面上的场强记为E(x),散斑图样通过物体1后继续传播距离Z2后到达平面2上的物体2,将物体2的光平面场强记为E(x′),再经过一定距离的传播后到达桶探测器,将桶探测器的光平面场强记为E(x′′)。通过计算即可得到到达桶探测器的总光强值为:

其中,h(x0,x)、h(x,x′)、h(x′,x″)分别表示光从可调制光源到平面1、平面1到平面2以及平面2到桶探测器的自由传播函数;T(x)和T(x′)分别表示物体1和物体2的透射函数。
由于散斑在传递过程中的光强涨落会发生变化,此时可以通过计算分别表示出物体1和物体2在所处平面上形成的光强分布,分别记为Ia(x0,x)和Ia(x,x′):

将式(2)、式(3)与式(2)、式(4)分别代入公式(1)中,即可得到:
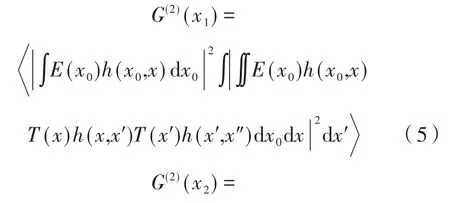
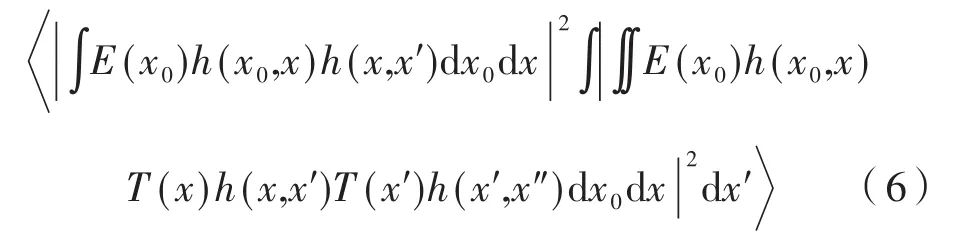
通过利用二阶关联函数,由于Ia在光的传播过程中发生变化,所以G(2)(x)的值也随着发生变化,如公式(5)和公式(6),则可以将物体1和物体2的信息分别突显出来,即可分别获得不同层面待测物体的信息。
由于光源是先经过物体1之后再传播到物体2的,所以到达物体2的光强会有一定的衰减,此时可以选用两个大小较为相近的物体进行成像,这样就可以保证有更多的光能够向后传播到达物体2,从而保证物体2可以成像。
2 数值实验
为了探究理论内容的可行性,是否可以利用鬼成像技术恢复前后两个层面待测物体的信息,则进行了数值仿真模拟。在数值仿真模拟过程中,首先选取两个大小较为相似的待测物体,但是后一个层面的待测物体比前一个层面的待测物体略大一些,待测物体为像素64×64 pixel的两幅灰度图片,箭头和圆圈。本文的数值模拟系统框架图如图3所示。在该系统框架图中,由投影仪投射出预先生成的正态分布的随机散斑图样,首先照射到前表面的待测物体箭头,然后带有随机散斑图样的透射光束向后传播到达后表面的待测物体圆圈,经过这样的一系列传播之后,最终的光强被桶探测器收集,并且传输给计算机,计算机会将桶探测器收集到的光强值与预先生成的随机散斑图样进行二阶关联运算,则可以恢复出前后两个层面的待测物体:箭头和圆圈。在数值模拟过程中,由于选取的待测物体的像素数为64×64 pixel的箭头和圆圈图片,所以需要进行的测量次数为4 096次,并且在进行完备测量的情况下噪声会非常小。图4为原始图像,白底黑色图片,图5表示利用鬼成像技术得到的两个层面待测物体的重构图像。

图3 数值仿真模拟系统框架图

图4 两个层面待测物体的原始图像

图5 利用鬼成像技术恢复两个层面待测物体图像的模拟结果
利用鬼成像技术恢复两个层面待测物体的重构图像的数值仿真结果如图5所示。当把两个待测物体放置在合适的距离处,通过一组测量则可以同时恢复出前后两个层面待测物体的信息,如图5(a)所示。为了确定后一层表面待测物体的具体信息,通过数值模拟得到图5(b)的重构图像,可以看出后层表面的待测物体为圆圈。该重构结果与图4中的原始图像一致。
在层析成像中,需要对不同层面的待测物体进行清晰成像。接下来选取三个大小较为相近的待测物体(箭头、圆圈和三角形)进行数值模拟实验。图6为三个层面待测物体的原始图像,图7为数值仿真结果。通过观察图7的数值模拟结果可知,可以通过计算鬼成像对位于三个层面的待测物体进行层析成像,并与原始图像相比较基本相符,从而证明了方案的可行性。通过观察模拟结果的背景信息可以发现,每个层面的重构图像的背景信息都有所不同,可能是由于散斑图样在传递过程中的距离分辨率不同而引起这种情况的发生,这为之后的研究工作提出了思路。

图6 三个层面待测物体的原始图像

图7 利用鬼成像技术恢复三个层面待测物体图像的模拟结果
通过观察和分析两次的数值模拟的结果可知,可以利用鬼成像技术在数值仿真实验中实现层析成像,并且能够清晰分辨出来多个层面待测物体的信息,证明了层析成像方案的可行性。
3 实验验证
图8为层析鬼成像实验系统装置图,图9为两个层面待测物体的平面直拍图。整个实验系统包括计算机、光源、两个待成像物体、毛玻璃和桶探测器。在实验的过程中由于投影仪发出的光散射角过大,在经过一段距离的传输后光斑变得过大,导致桶探测器无法接收到所有从投影仪投射后经过一系列传播后的光信号,所以在待测物体后放置毛玻璃,可以将光信号进行整合,以获取更多的光强信息。本实验选取4 096张像素数为64×64 pixel哈达玛散斑图样作为照明图样,通过调节投影仪使照明散斑照射到两个层面的待测物体上,随后穿过物体的透射光经过毛玻璃并最终被桶探测器接收,通过在计算机上将探测结果与散斑图样进行关联运算,实现对待测物体的重构。图10为经过计算机的关联运算得到的待测物体的重构图像。

图8 层析鬼成像实验系统装置图

图9 两个层面待测物体的平面直拍图

图10 利用层析成像实验装置图的重构图像
从实验结果可以看出,可以利用计算鬼成像技术分别获得两个层面的待测物体的重构图像,如图 10(a)和图 10(b)所示。在该实验中得到的待测物体的重构图像与原始图像基本相符。三层待测物体的实验结果与二层待测物体的实验结果基本相似。
通过观察与分析实验结果可以发现,可以利用鬼成像技术在实验中对待测物体进行层析成像。通过比较与分析数值仿真结果与实验验证结果,二者的结论基本一致,则可以证明利用鬼成像技术进行层析成像方案的可行性。
4 结论
本文首先阐述了利用鬼成像技术进行层析成像的理论模型,然后依据理论分析进行数值仿真模拟。通过观察和分析数值模拟结果可知,可以利用计算鬼成像技术进行一次探测,即可重构出多个层面待测物体的信息。综上所述,本文证明了利用鬼成像技术进行层析成像方案的可行性,且实验设备简单,易于实现。恢复不同层面待测物体信息在多个领域有着较高的实用价值和广阔的应用前景,为层析成像提供了一种新的成像方案,也为三维鬼成像技术的发展奠定了基础。
——随钻钻孔电磁波层析成像超前探水设备及方法研究

