基于鬼成像技术的光谱增强研究
闫凌浩,王晓茜,邵嘉琪,高超,刘娜
(长春理工大学 物理学院,长春 130022)
鬼成像是一种间接的成像方法,它通过空间强度相关性测量来获取物体的信息,对比传统成像来说,具有抗噪声能力强、高分辨率、突破衍射极限等优势,近些年来成为大家竞相研究的热门问题。1995年,Pittman等人[1]设计了纠缠双光子成像,现在认为纠缠双光子成像的出现标志着鬼成像技术的正式诞生。2005年,Valencia等人[2]提出了赝热光源鬼成像,满足了热光源的空间涨落性质。2008年,Shapiro提出了单光路鬼成像方案[3],将其称为计算鬼成像。该方案利用计算机直接控制空间光调制器件,从而对光源实现调制,代替了传统鬼成像系统中的参考光路,简化了鬼成像的成像系统。2010年,Ferri等人[4]首次提出差分鬼成像方案。差分鬼成像是利用两臂探测器的差分信号进行关联运算,通过对差分信号的关联运算,可以有效地消除噪声,大大提高了基于热光源鬼成像系统的信噪比,首次将鬼成像技术应用于弱吸收物体成像。2019年,Bornman N等人[5]提出了一个基于纠缠交换系统的鬼成像,为二维空间状态在量子网络中的隐形踹太提供了途径,同年,Hodgman等人[6]构建了高达五阶的高阶重构图像,并证明使用高阶相关性可以在不影响分辨率的情况下提高图像的可见性。2021年,Zhang N等人[7]提出了使用逐点方法的新的局部二元鬼成像,该方法可以补偿二值化过程中信息丢失导致的成像质量下降,与传统鬼成像对比可以较好地重建目标细节。
鬼成像技术发展一段时间之后,大多数学者都是以单一波长的光源进行实验,直到2013年,Welsh[8-9]通过实验进行了多波长压缩重影成像的实验,得到了真实的多波长高质量重建,证明了鬼成像可以实现多波长、多分量、全色的真实物体荧光形象。同年,曲阜师范大学的段德洋[10]实验验证了多波长成像的彩色重构明显优于单色图像,而多波长鬼成像除了对色彩重构之外,多波长鬼成像与光谱成像的结合也受到了学者们的关注,2014年,吴建荣等人[11]提出了基于相位调制的单次曝光压缩感知成像,该方案具有较高的图像获取效率,但是会导致成像质量大幅度降低。为了提高多光谱图像的重建质量,次年,该小组提出了基于先验图像约束的多光谱压缩感知(PICHCS)[12],该方案在低采样率低信噪比的条件下,能够提高多光谱图像的重建质量,2017年,该小组提出了基于稀疏约束的鬼成像光谱相机[13],但是该系统受探测器位置影响,会影响重构图像的光谱分辨率,为解决上述问题,刘盛盈等人[14]提出了基于平场光栅的稀疏约束鬼成像高光谱相机,该方案可以实现分别调控光谱分辨率、空间分辨率以及信噪比,提高重构图像质量。同年,刘震涛[15]提出了基于稀疏和冗余表象的鬼成像光谱相机,提高了光学成像系统的图像信息获取率。
光谱特征提取是从已经得到的物体的原始光谱数据中除去多余的信息而保留有用的特征信息,一些传统的特征提取方法,例如主成分分析法、边界判别法等都是基于统计的特征提取方法,在使用这些方法时要求有足够多的训练样本作为保障,而本文以多波长鬼成像的关联函数为理论基础,在理论上推导了可以利用鬼成像技术增强出某些特定波长的光谱图像,并且进行了数值模拟以及实验验证,成功地证明了鬼成像技术是可以增强某些特定光谱的信息,解决了当滤波器的带宽过窄导致获取光强较弱,使得有可能湮没在噪声当中,导致无法获取到相应的信息的问题。
1 理论分析
多波长鬼成像系统需要物体的波长信息,为了简单起见,使用多波长的光源对物体进行照射,此时光源中包含多个波长的信息,而在探测臂,桶探测器的前端需要不同频带宽度的滤波片进行滤波,从而获得某些频宽的光强,此时的二阶关联函数可以表示为:

式中,IR(x,y)为CCD获取的光强;IB为桶探测器的探测值
将获取的信息通过上式计算就可以得到某个波长的信息的光谱图像,而对于光谱图像来说,往往希望光谱分辨率越高越好,也就是意味着此时的桶探测器前的滤波器的带宽越窄越好,但如果滤波器的带宽越窄,意味着获取的总的光强值越弱,想要获取的信息就有可能淹没在噪声当中,因此本文试图采用几个宽带滤波片,通过相应的运算,将其中某些窄带的光谱图像重构出来。
实验中,采用投影仪作为实验光源,投影仪投射的光斑是黑白的散斑,此时所有波长的强度信息基本相同,即:
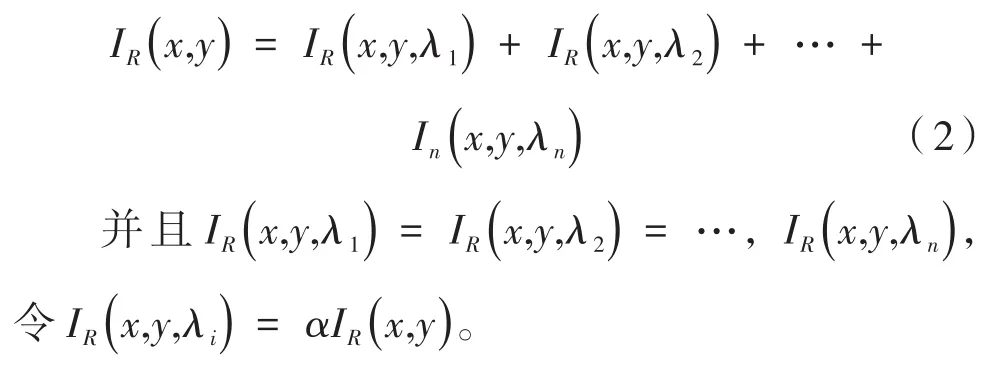
桶探测器前面放置相应的宽带滤波片,把要测量的窄带光谱信息的中心波长记为λ1,λ2,…,λn,此时宽带滤波片包含了相应的波长信息,首先考虑两个宽带滤波片的情况,分别为桶探测器1和桶探测器2,此时桶探测器1的光强信息可以写为:

将公式(3)和公式(2)代入公式(1)中,可以得到通过桶探测器1所获得的二阶关联函数,即:

此时可以发现,G(2)(x,y,λ1,λ2)是包含G(2)(λ1)+G(2)(λ2)的二阶关联函数,这意味着鬼成像的重构图中应该包含λ1和λ2的光谱信息,同理,通过桶探测器2可以得到的二阶关联函数表示为:
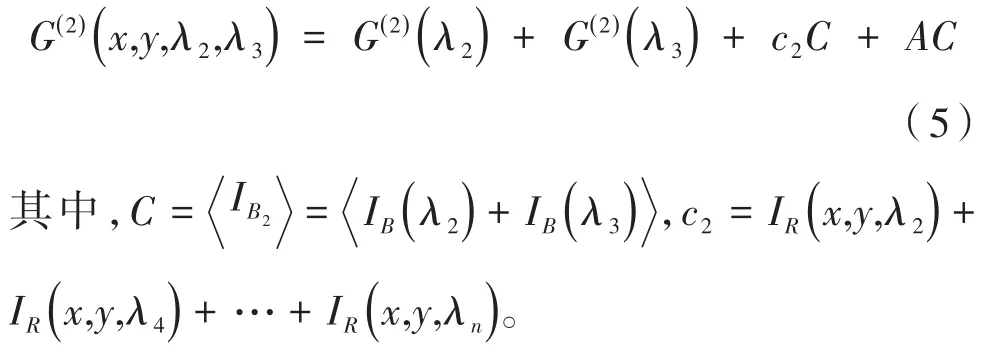
这里希望通过两个宽带滤波片增强某些窄带的信息,假设想要获取到λ2的光谱信息,通过观察式(4)以及式(5)可以发现,通过二阶关联函数很难分辨出λ2的光谱信息,接下来引用三阶关联函数来获取相应的光谱信息,此时三阶关联函数的表达形式为:

将式(2)和式(3)代入到式(6)中可以得到:

通过公式(7)可以发现,此时的三阶关联函数是关于λ1和λ3的二阶关联函数的重构图以及关于λ2的三阶关联函数的重构图,可以证明通过计算三阶关联函数可以有效地增强关于λ2的信息,也就意味着通过两个宽带滤波片可以增强中间某个窄带的光谱信息。下面根据理论推导进行数值模拟。
2 实验结果与讨论
基于以上理论和分析,证明了使用具有重合波段的宽带滤波片代替窄带滤波片进行波长筛选,通过计算三阶关联函数来重构图像,可以有效地增强重合波段的光强,也就是说可以获得更好的光谱图像,接下来根据理论推导,进行数值模拟。
首先,利用随机散斑作为照明光源,将图1、图2、图3作为待测物体,分别为具有三个不同中心波长λ1、λ2和λ3的物体,为了方便计算,将所有的图像都设为二值图像,此时由于投射的散斑是黑白的,所以此时的波长信息基本相同,然后利用随机散斑作为照明散斑进行数值模拟。

图1 中心波长为λ1的物体的二值图像

图2 中心波长为λ2的物体的二值图像

图3 中心波长为λ3的物体的二值图像
根据公式(4)和公式(5)中的二阶关联函数的表达式,可以重构出G(2)(x,y,λ1,λ2)和G(2)(x,y,λ2,λ3)的空间信息,如图4、图5所示。由图4可以看出,此时的G(2)(x,y,λ1,λ2)完全恢复出了λ1和λ2的光谱图像,但是此时这两个图像的强度基本一致,导致没有办法区分这两个图像的差异,并且对于这两个待测物体的图像原本是二值图像,而重构出来的图像变成了灰度图像,这是由于公式(4)中会有一项(c1+A)B的背景像,由于该背景像的存在,导致重构图像变得不清晰。图6为二阶关联函数G(2)(x,y,λ2,λ3)的重构图,此时可以发现图5中重构出来的是λ2和λ3的光谱图像,此时两个图像的强度与图4中图像的强度基本一致,并且也会存在相同的背景像,从而导致图像的可见度变弱,此时可以发现此时理论与数值结果符合得比较好。

图4 二阶关联函数G(2)(x ,y,λ1,λ2)的重构图

图5 二阶关联函数G(2)(x ,y,λ2,λ3)的重构图
为了能够进一步凸显出λ2的光谱信息,进一步模拟了三阶函数的形式,如图6所示,可以看出此时的三个图像都可以在重构图中恢复过来,并且可以发现此时的三个图像的灰度并不一致,其中λ2的光谱图像的亮度最高,根据公式(7)可知,这是由于对于λ2的信息所获取到的是三阶关联的信息,而对于λ1和λ3的光谱图像的强度是明显小于λ2的,并且λ1和λ3的光谱图像的可见度也有差别,通过公式(7)可以发现G(2)(λ1)和G(2)(λ3)的系数与λ1和λ3的透过率有关,透过率越大,光谱图像的可见度就越高。通过数值模拟可以清晰地发现,重合波段部分的图像质量明显优于二阶重构图,也就是说,采用多个宽带滤波片可以增加重合波段的光强,并且可以使重合波段的重构图像的成像质量效果更好。

图6 二阶关联函数G(3)(x ,y,λ1,λ2,λ3)的重构图
通过理论分析以及数值模拟可以证明如果想获得较窄带宽的光谱图像,当光强较小导致容易湮没在噪声当中使得无法获取图像时,使用多个宽带滤波片进行波长筛选,相对于窄带滤波片,可以有效地增强想要得到的波段的信息,也就是说可以获取比较好的光谱图像。
接下来进行实验验证,基于以上的理论分析以及数值模拟,如图7、图8所示搭建实验平台。
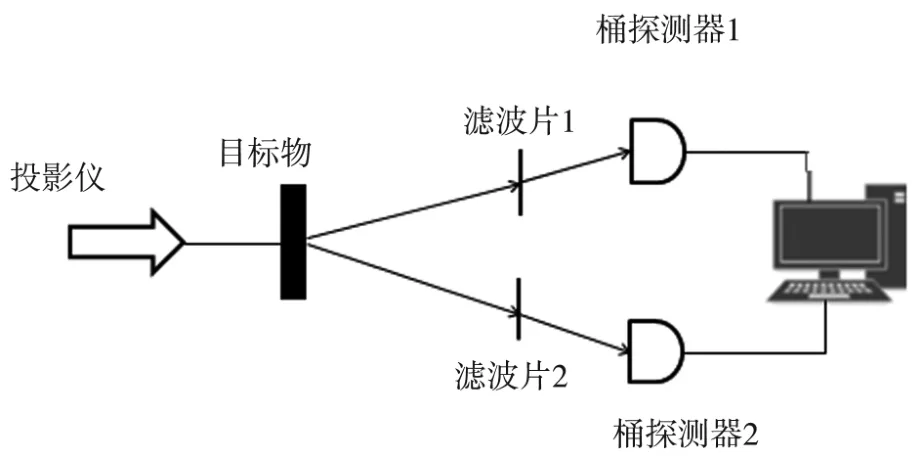
图7 实验装置图

图8 实验实物图
为了更好地描述波长的信息,选用中心波长为450 nm、520 nm以及570 nm的窄带滤波片作为待测物体,如图9所示,区域1、2、3分别对应中心波长为450 nm、520 nm以及570 nm的窄带滤波片,桶探测器1和桶探测器2前放置带宽为400~532 nm以及500~600 nm的宽带滤波片进行波长筛选,接下来利用计算机生成的随机散斑作为实验照明图样,然后使用投影仪将照明图样投放到待测物体上,计算鬼成像的实验重构图如图10、图11所示,通过观察实验重构图可以看出,图中的中心波长为420 nm以及520 nm的窄带滤波片的重构图明显比中心波长为470 nm的窄带滤波片的重构图的成像效果要好,而在图12中,中心波长为470 nm的窄带滤波片的重构图成像效果明显提高,相应的其余两个窄带滤波片的重构质量有所下降,也就是说成功地增强了中心波长为470 nm的窄带滤波片的信息,与理论分析和数值模拟的结果相符合。

图9 实验待测物体

图10 二阶关联函数G(2)(x ,y,λ1,λ2)的重构图

图11 二阶关联函数G(2)(x ,y,λ2,λ3)的重构图

图12 二阶关联函数G(3)(x ,y,λ1,λ2,λ3)的重构图
3 结论
本文以多波长鬼成像中光谱增强的理论分析为基础,通过数值模拟以及实验验证,解决了当想要获得较窄带宽的光谱图像但由于光强太小容易被湮没在噪声中导致无法成像的问题,并且在得到较窄带宽的光谱图像的同时可以增强特定频宽的光谱图像,发现通过鬼成像技术可以增强某些特定光谱的信息,为鬼成像技术与多光谱成像技术的结合奠定了基础。

