改进全自适应遗传算法的加速度计新标定方法

于海燕， 李 宇

（郑州科技学院a.信息工程学院；b.电子与电气工程学院，郑州 450064）

0 引 言

随着微电子机械系统技术的不断发展，微惯性测量单元在未来导航的各个领域势必会得到越来越广泛的应用［1-2］。尤其在导航领域，加速度计（Micro-Electro-Mechanical System，MEMS）因其低功耗和小体积得到了较广的应用，应用中需通过标定来减小其对导航精度的影响［3-5］。

对MEMS的标定研究产生了众多方法，Lotters等［6］通过转换方法的求解完成对加速度的标定。Frosio等［7］通过牛顿迭代法对加速度计进行了标定，但未交代初值该如何选择。Tedaldi等［8］提出了LM算法也可完成对加速度计的标定，但过于繁琐的计算限制了其发展。Zheng等［9］提出了一种双轴转动惯导部分误差的八位置系统标定方法。Xiang等［10］提出一次电标定算法，这种算法可利用自身的旋转机构结合旋转惯导的特点实现系统的自标定。Chen等［11］提出了一种单轴旋转惯性导航的快速变换算法，该算法可以校正单轴旋转惯性导航的误差。郭卫等［12］设计了BP网络的标定方法，但是该方法需要保持大量的训练，这就降低了效率。高爽等［13］引入了自适应遗传算法（Adaptive Genetic Algorithm，AGA），标定后解算的水平姿态角精度可达0.1°，但并没分析缺算法收敛性对遗传算子产生的影响。同年，韩洪祥等［14］通过三轴转台实现了无定向MIMU误差系数的标定，虽然提升了标定的准确性，但受制于成本，并未广泛应用。邹泽兰等［15］提出了一种改进的自适应遗传算法，相比经典牛顿法其模值RMSE降低了22.2%，同样的方法可以借鉴，通过遗传算子的改进提高标定精度。

上述方法虽然可以完成对加速度计的标定，但使用的MEMS标定方法复杂度较高，转台设备使用成本大，应用效果不佳。由此，本文设计了改进遗传算子，通过改进遗传算法、确定了全自适应遗传算法（TAGA）的最优，并将其与经典牛顿法进行对比，实现对标定问题的转换。同时用仿真实验进行验证其有效性。

1 改进全自适应遗传算法

1.1 改进遗传算法的设计

本文对MEMS标定方法，在自适应遗传算法思想的基础上对算法进行了改进，算法流程如图1所示，通过对多个算子的迭代收敛确定全自适应遗传算法的最优。

1.2 全自适应遗传算法

常用的寻优方法大多是在目标函数梯度上搜索，迭代效率不高，容易陷入局部最优，影响到了使用的效果。遗传算法是在自然选择的基础上形成的，根据初始化的个体来对生物进化过程进行模拟，基于个体的进化获得质量最高的个体，通过这种方式得到需要的最优解。该算法在非线性控制系统优化中具有一定的应用潜力。传统遗传算法如标准遗传算法（Standard Genetic Algorithm，SGA）、自适应遗传算法AGA及改进的自适应遗传算法（Improved adaptive genetic algorithm，IAGA）在应用时会出现早熟、容易陷入局部最优及后期搜索迟钝等。综合考虑到上述问题，引入了全自适应遗传算法（Totally Adaptive Genetic Algorithm，TAGA），通过这种方式来改善搜索能力，即交叉概率

式中：F为种群中2个进行变异的个体的最大适应度；Fmean为整个种群的平均适应度；n为遗传算法当前工作过程中的迭代次数；nmax为遗传算子在工作过程中的最大迭代次数；Pb为变异概率，在遗传算法初始化时可以将最小变异概率Pbmin设置为0.001，最大变异概率Pbmax设置为0.1。

根据式（1），在MATLAB仿真环境下对3种算子进行仿真分析，经过200次的迭代得到的收敛结果对比如图2所示。

由图2可知，3种算子的收敛速度有明显差异，当迭代达到50次时，TAGA具有明显的收敛趋势，当迭代次数为80次时彻底收敛。而IAGA收敛结果未达到最佳，AGA陷入局部最优。因此，本文采用全自适应TAGA算子。

2 加速度计标定模型及误差模型

2.1 建立标定模型的误差因数

加速度标定模型受到加工工艺等因素的影响，三轴MEMS往往会形成一定的非正交误差，如图3中所示。图3中，s和b是2个坐标系，Xs，Ys，Zs代表非正交坐标系；Xb，Yb，Zb代表正交坐标系，已知Zb、Zs对齐，O为中心点。另外，静态零偏、比例因子均会对加速度计测量产生影响，均需进行标定。同时，外界环境及加速度计本身的抖动会产生噪声，本文采用平均静态数据的方法尽可能消除噪声带来的影响。

2.2 误差模型的建立

静止时，加速度计的误差模型可表示为

将其写成矩阵形式即为加速度计标定的数学模型：

式中：fx，fy，fz分别为x，y，z方向加速度计的输出；a0x，a0y，a0z为x，y，z方向加速度计的零偏；ax，ay，az为x，y，z方向加速度计的输入；Kax，Kay，Kaz为x，y，z方向加速度计的标度因数；Kaxy，Kaxz，Kayz，Kayx，Kazx，Kazy为加速度计的安装误差。

3 传感器标定实验

3.1 实验环境

本文采用自制的MEMS惯性测量单元测试标定设备MEMS IMU（型号：MZ 812 8960）。该设备能提供精确的速率、位置、摇摆等运动控制，并且能够实时采集存储测试设备的姿态角和惯性测量单元的数据信息。测试标定系统不但可以为MEMS加速度计的标定提供恒定转速，通过上位机控制三轴测试标定设备的内框、中框、外框以固定步长旋转固定时间；而且还可为MEMS加速度计的静态位置实验提供精确位置，通过上位机控制标定测试设备内、中、外框转到精确的方位；当惯性测量单元在标定测试时，还可做为惯性测量单元姿态测试信号源。测试标定系统如图4所示。

3.2 实验结果

在标定时需要先将Z轴向上，然后在水平面中逐次顺时针旋转90°，继而得到4个部位的数据。按照类似的方式分别得到Y轴上、Z轴下、X轴上、X轴下、Y轴下的各个数据，其中零偏用B表示，标度因子用S表示，非正交误差用M表示。各位置采集时间为15 s，总计24个位置。参数设置见表1，初始标定的数据采集完成之后传输到上位机中进一步进行处理与分析。

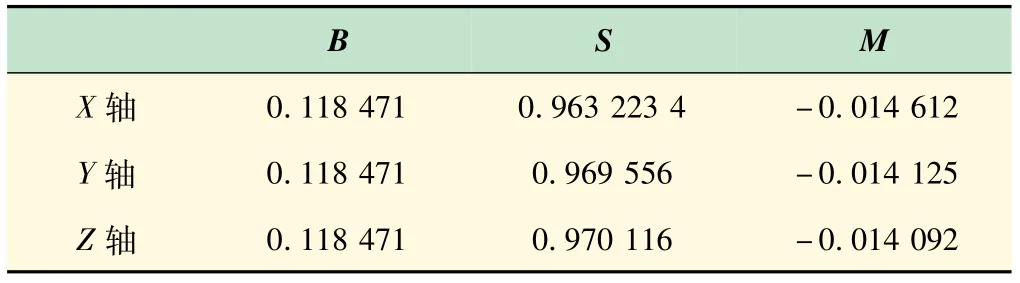
表1 参数设置

采集数据结束后，采用了本文设计的方法开始标定加速度，基于TAGA算法进行处理后得到最优参数。最终得到如图5所示的适应度曲线。

由图5可知，在迭代数达到80时，基于TAGA的算法已经收敛，由此可以认为该算法在收敛速度上具有很明显的优势，而最佳适应度基本保持在10-3数量级，相对于适应度均值存在显著的差异性。

图6为参数标定的结果，由图可知，在迭代完成时各个参数基本已经收敛，因此在之后的导航中可以采用得到的寻优结果。

针对得到的零偏、标度因子及非正交误差3个参数进行验证，对相同IMU的5个位置进行数据采集，总计持续180 s，然后对模值进行计算，采用本文算法和经典牛顿法得到的标定结果如表2。

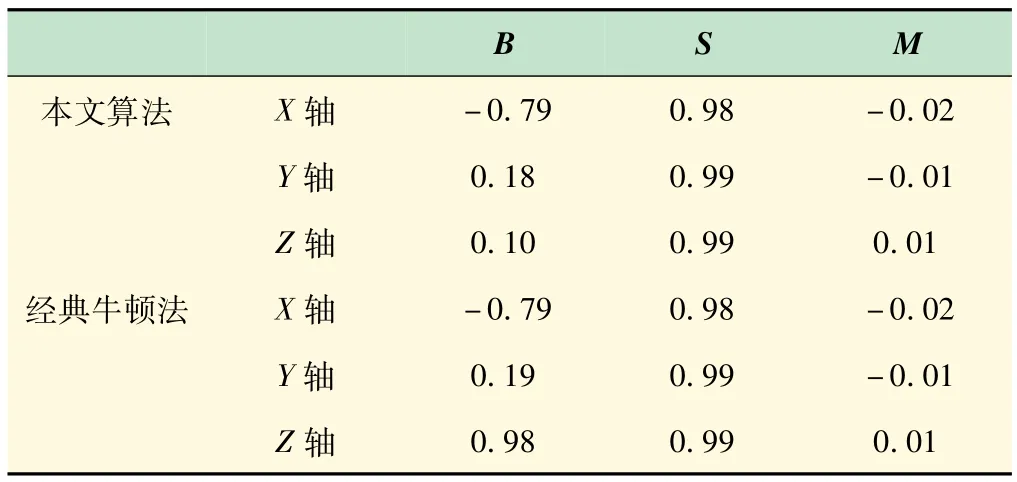
表2 本文算法和经典牛顿法的标定结果对比

本设计算法标定之后的模值较标定前的标准差从118.21 mg减小至1.19 mg，取得了良好的效果。而牛顿法标定之后的模值较标定前的标准差从118.21 mg减小至1.65 mg。可看出，2种算法的标定效果体现出一定的差异性，在模值标准差上前者相对于后者更小，两者的偏差为27.9%，由此证明了本文算法在标定上取得了良好的效果。

图7为不同方法的模值对比结果，由图可知，标定之前与重力真值存着较大的差距，两者的偏差基本达到了1.1 g，通过2种方法标定之后与真值保持了较高的一致性，相对于经典牛顿法，本次设计方法更接近于真值，偏差基本保持在0.38 mg上下。

4 结 语

本文设计的三轴MEMS标定算法，通过其改进的自适应遗传算法，使其具备了动态变化的特征，即随着迭代数而改变，改善了收敛性；同时解决了陷入局部最优的问题，便于得到全局寻优的结果。同时，通过实验验证了本文设计方法的有效性，结果表明，标定之后模值标准差指标为1.19 mg，相对于经典牛顿法减小了27.9%，结果显示与当地重力值基本一致，适合于应用到实际的导航中。在后续的研究中需要重点关注适应度函数的研究和应用，通过对其进行优化进一步提升算法的寻优效果。