微电网最小化通信链路优化算法

刘明宇， 李晓丽， 王千千

(东华大学 信息科学与技术学院， 上海 201620)

微电网由多种分布式电源、储能、负载以及相关监控保护装置构成，既可以与电网并网运行，也可以孤岛运行。作为一种新的电网结构，微电网的出现顺应我国高质量的新发展理念。将多种分布式电源以微电网的形式集成并灵活并网是利用分布式电源的有效方式[1-4]。基于分布式一致性理论，将微电网中的分布式电源抽象成多个智能体，在多智能体中变量随时间变化趋于一致的收敛速度显得尤为重要，系统的收敛速度主要取决于多智能体连通图拉普拉斯矩阵的第二小特征值(又称代数连通度)。在此基础上，Bidram等[5-6]利用神经网络理论研究微电网二次控制自适应等问题。李远哲[7]提出一种基于网络拓扑优化的多微电网系统分布式协同控制方法，该方法在强化学习的基础上利用Q-learning算法实现拓扑结构的优化，旨在实现微电网群的全局协同控制，并消除中央控制器的必要性，但是需要大量的数据支撑。沈政委等[8]就改变拓扑结构工具的输电线的若干开断问题和电网电压的控制问题进行了综述，但是没有给出具体的算例分析和解决方案。吕振宇等[9]提出一种利用一致性算法对微电网二次控制进行优化的方法，但是在实现拓扑优化的算法中采用了传统的Warshall算法，该算法的缺点在于运算速度慢，在微电网中的应用规模较小。于芃等[10]对微电网并网、离网切换问题进行了模块化分析，实现了平滑切换，但是本质上没有改变拓扑结构，因而系统的收敛速度和通信成本不变。

为了降低微电网运行的通信成本，在传统微电网控制的基础上，对微电网通信层的拓扑结构进行链路最小化分析。将分布式电源抽象成多智能体，在图论的技术上着重研究各个节点的通信连接方式对系统的收敛速度的影响，利用灵敏度和梯度下降思想设计一种通信链路最小化算法。该算法对系统连通图的边进行适当删减，在保证拓扑结构为全连通图的前提下，最大化代数连通度，最小化通信连接的边数，从而将微电网的通信成本降到最低。

1 微电网控制的数学模型

分布式电源的控制策略直接决定微电网能否稳定运行，风力发电系统、光伏发电站、微型燃气机及储能系统等作为分布式电源通过电力电子变流装置并入大电网，使得微电网在常规模式下具有两种运行状态，即并网运行和离网运行，后者又称孤岛运行。在微电网无功功率分配的基础上进行链路最小化分析。

一般孤岛运行的微电网采用下垂控制解决功率的分配问题，下垂控制通过模拟传统发电机组的功频特性，使所有分布式电源共同参与功率分配以维持系统频率和电压的稳定。通常将微电网中的分布式电源与母线连接简化成图1所示电路，其中：Ub∠0为公共母线的电压(符号∠为电气工程中相位符号)；U∠δ为分布式电源的输出电压；δ为电压功角；Z∠θ=R+jωL为分布式电源的等效阻抗；S为分布式电源的视在功率；P和Q分别为有功功率和无功功率。

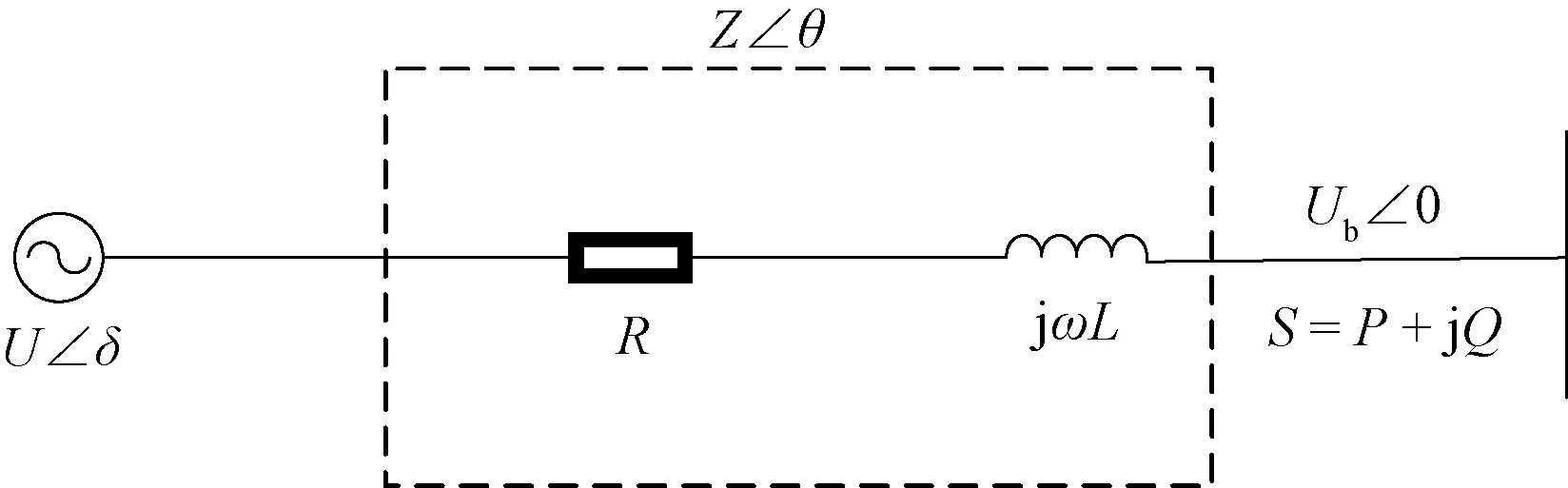
图1 单台分布式电源功率传输示意图

由图1可知，传统的分布式电源通过线路阻抗R+jωL消耗部分有功、无功功率连接至母线上。当微电网中分布式电源到母线的输出阻抗呈电感性状态时，输出的有功功率和无功功率如式(1)所示。

(1)

式中：U为输出电压幅值；X为阻抗幅值。

为研究线路阻抗在电感性条件下的功率分配问题，用频率代替电压功角δ，下垂控制表达式为

(2)

式中：Pref和Qref分别为下垂控制分布式电源输出的有功功率和无功功率的参考值；P0和Q0分别为分布式电源的额定有功功率和无功功率；f0和U0分别为分布式电源的额定频率和电压；f和U分别为分布式电源的实测频率和电压；mf和nu分别为频率-有功功率和电压-无功功率的下垂系数。基于f-P和U-Q的下垂控制框图如图2所示。

图2 基于f-P和U-Q的下垂控制典型结构图

由式(2)得出相应的频率和电压下垂曲线，如图3所示。

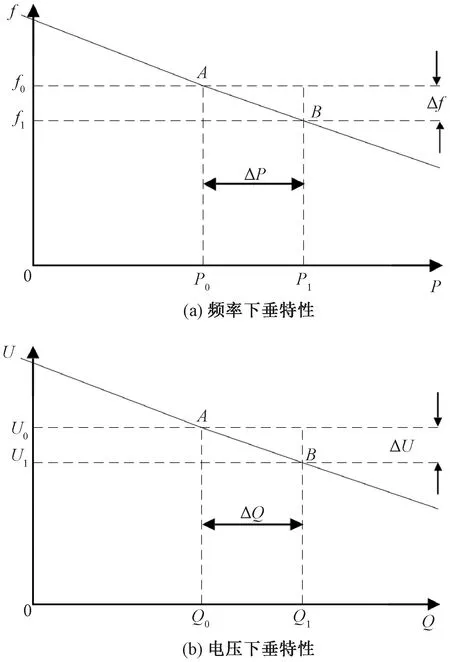
图3 下垂特性示意图

发电机功率的额定值根据视在功率确定，无功功率不平衡必然会引起发电机视在功率的不平衡，同样会限制发电机组容量的发挥，特别是对于功率因数较低的电站，机组的带负载能力不是取决于发电机的额定功率，而是发电机的额定电流。无功负载的不平衡也可以将其不均衡部分看成是两台发电机之间的一种环流，在发电机内部产生附加的损耗，甚至使发电机过载。

在传统的下垂控制下，各分布式电源连接到母线上的线路阻抗不相等会造成无功功率分配不均，若有两台并联的分布式电源，其容量相同但是线路阻抗Z1>Z2，则会出现如图4表示的功率分配情况。由图4可知，分布式电源的线路阻抗不等会造成无功功率分配不均，且线路阻抗越大，分布式电源无功功率越小。

图4 线路阻抗对无功功率分配的影响

2 分布式一致性理论在微电网中的应用

在分布式控制理论中，图论通常起到载体的作用。一般情况下，用有向图G=(V，E，A)表示由n个多智能个体组成的通信网络；V={1,2,…,n}表示该图中所有节点构成的集合；E⊂V×V表示各个节点相连边；A=[aij]表示邻接矩阵，若图中的节点j向节点i存在连接则进行信息交互，aij≠0，反之，二者没有连接不进行信息交互，aij=0；Ni={j∈V|(j,i)∈E}表示与节点i有信息交互的节点的集合。定义节点i的出度和入度分别为degout,degin，则有：

(3)

在微电网信息层内由通信网络和多智能体构成的连通图中，各节点相互连接的边构成的拓扑结构显得尤为重要，连接的边数太少会导致系统的收敛速度变慢，连接的边数过多将导致系统的通信成本增加，产生不必要的浪费。

出度元素在主对角线组成的矩阵为有向图G的D矩阵，与信息交互相关的拉普拉斯矩阵L可表示为L(G)=L=D-A。若G中任意节点的出度值与入度值相等，则称G为平衡图，L满足LI=0且ITL=0，其中I为n阶单位列向量。若有向图G每条边都是双向的，则(i,j)=(j,i)，即节点i与j可以互相通信，称为无向图，无向图是平衡图的一种形式；若有向图G任一节点都可以找到一条路径到达其他节点j，则称为连通图。

在微电网中可以将分布式电源抽象成多智能体的网络节点，分布式电源彼此之间相互联系。假设Qi为节点i的无功功率状态变量，则可以得出以下控制策略：

(4)

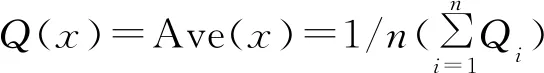
(5)

将一致性算法加入至微电网中的控制框图，如图5所示。

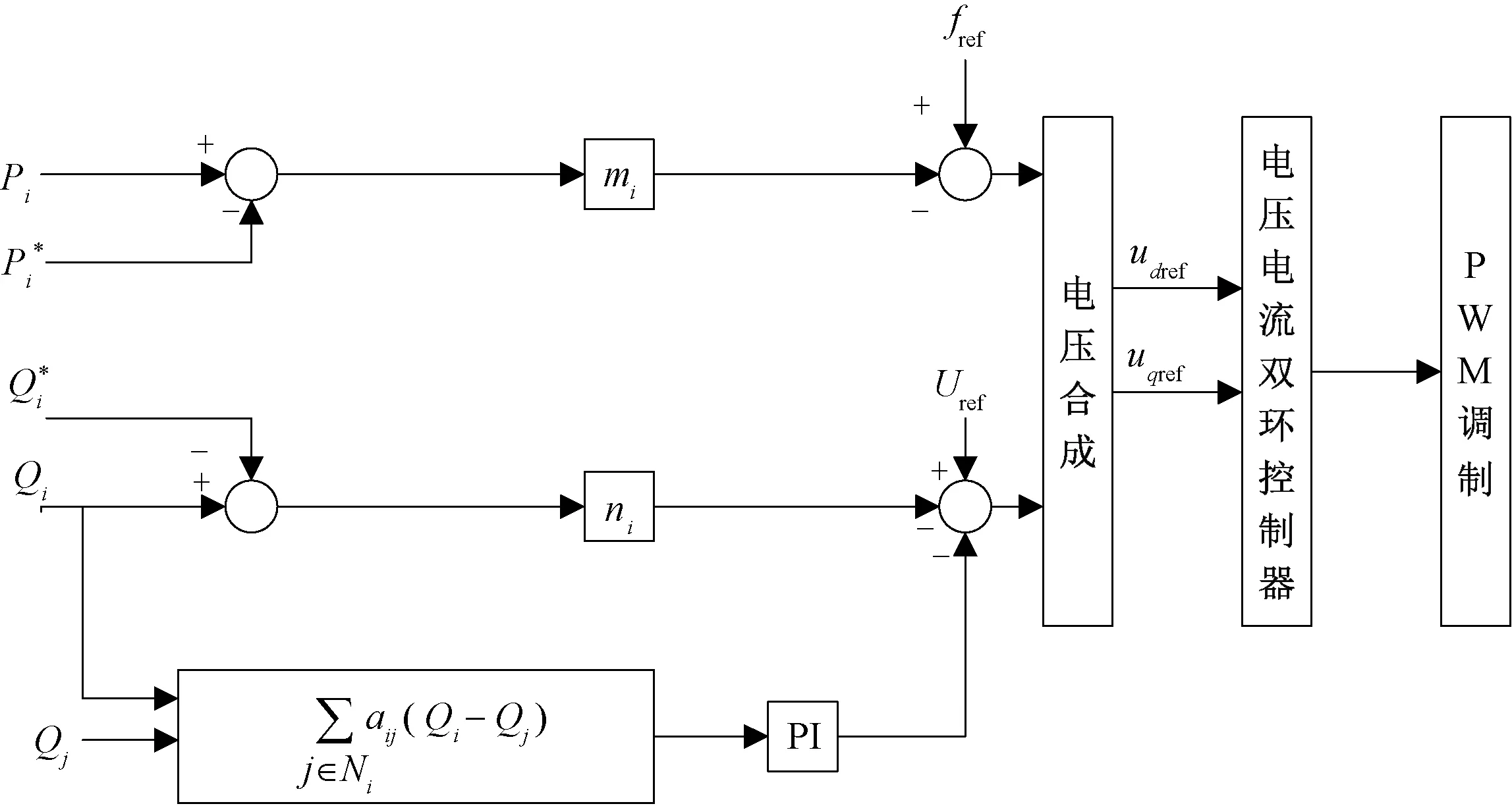
图5 一致性算法应用于分布式微电网的控制框图

加入一致性算法后微电网的无功功率分配示意图如图6所示，其中KP为原始的下垂曲线，KP1和KP2分别为经过一致性算法调整的两台分布式电源的下垂曲线，其中线路阻抗Z1>Z2。

图6 加入一致性算法后微电网的无功功率分配示意图

对比图4所示的下垂控制的无功功率分配可知，未加入一致性算法时，两台分布式电源的无功功率分别为Q1和Q2，没有实现无功均分。加入一致性算法后两者的无功功率(Qref)相等，实现了无功均分。

图7描述了微电网的信息层和物理层，其中上层为微电网的信息层，信息层将微电网的分布式电源抽象成多个节点相连的网络，其负责各个分布式电源之间的信息传输与传递。

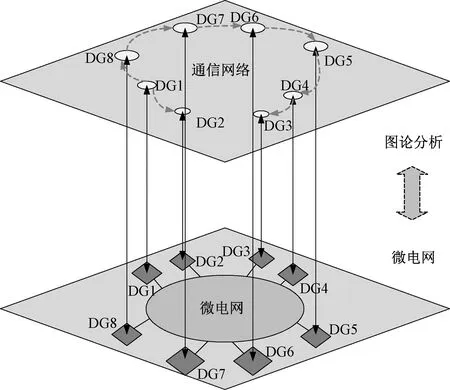
图7 微电网图论分析

系统的收敛速度与连通图的拉普拉斯矩阵的第二小特征值相关，具体证明如下：

在一个无向连通图G中建立拉普拉斯状态不一致函数：

(6)

根据文献[11-12]，网络状态不一致的相对收敛性有以下特性：

(7)

因为G为无向图，所以rank(L)=n-1；根据Gerschgorin原理，L的n个特征值可以表示为0=λ1(L)<λ2(L)≤…≤λn(L)≤2Δ，Δ代表系统的最大出度，即Δ=maxidegout(vi),vi为分布式电源的出度。由式(6)可知，各个节点状态不一致的收敛速度与拉普拉斯矩阵的代数连通度λ2(L)有关[13]，各个节点动态状态为x=α1+η，其中α=Ave(x)对应于系统的稳定状态，各个节点的最终状态收敛于系统的平均值；η为状态不一致向量，满足1Tη=0，1=[1,1,…,1]T。在Lyapunov函数中V(η)=‖η‖2/2，可得式(8)。

(8)

3 最小通信链路模型与算法

分布式微电网拓扑结构优化的目标为：在原来拓扑结构的链路下，为减少通信成本，在代数连通度减小量最小的情况下寻找一种最小生成树，即拓扑结构的连边数最少。具体数学模型如式(9)所示。

(9)

(10)

则λ2可表述以下推理：

(11)

式中：λ2(L1(μ))对应的单位右特征向量记为v2。

根据式(9)，λ2(L1(μ))对于μ的梯度为

(12)

由于L1=L-μLI是一个实对称矩阵，则有如下推导：

(13)

因此有：

(14)

根据式(9)和(12)得出以下结果：

(15)

因此，希望删除的边权值μ造成代数连通度减小量Δλ2为最小，每次操作都会使得该拉普拉斯矩阵的第二小特征值减小量最小化，将上述删除边权值μ的过程进行循环，直至更新后的拓扑结构图的代数连通度减小到0为止。提取上一次循环的连通图作为更新的拓扑结构，根据以上推导及结论设计最小化通信链路算法。

最小化通信链路算法：

Step 1L=L(G),μ=0.1，i=0;

Step 2 whilei<10

L1′=L(G)-μLI,i++，L2′=L2′-L(G)

Step 3 Findmax{L2′(i,j),i≠j}

Step 4 删除Step 3对应的边，形成新的拓扑L=L1(G′)，代数连通度为λ2′

Step 5 ifλ2′>0,置L(G)=L1(G)

else 优化拓扑结构为L(G)。

为了检验该算法在普遍系统拓扑结构中的有效性，给出以下算例分析。随机生成30个节点和93条链路的系统拓扑结构如图8所示。

图8 随机生成的拓扑结构图

经最小化通信链路算法删除部分链路后的拓扑结构如图9所示。优化后的拓扑结构共删除64条链路，剩余链路为29条，为这30个节点的最小生成树。

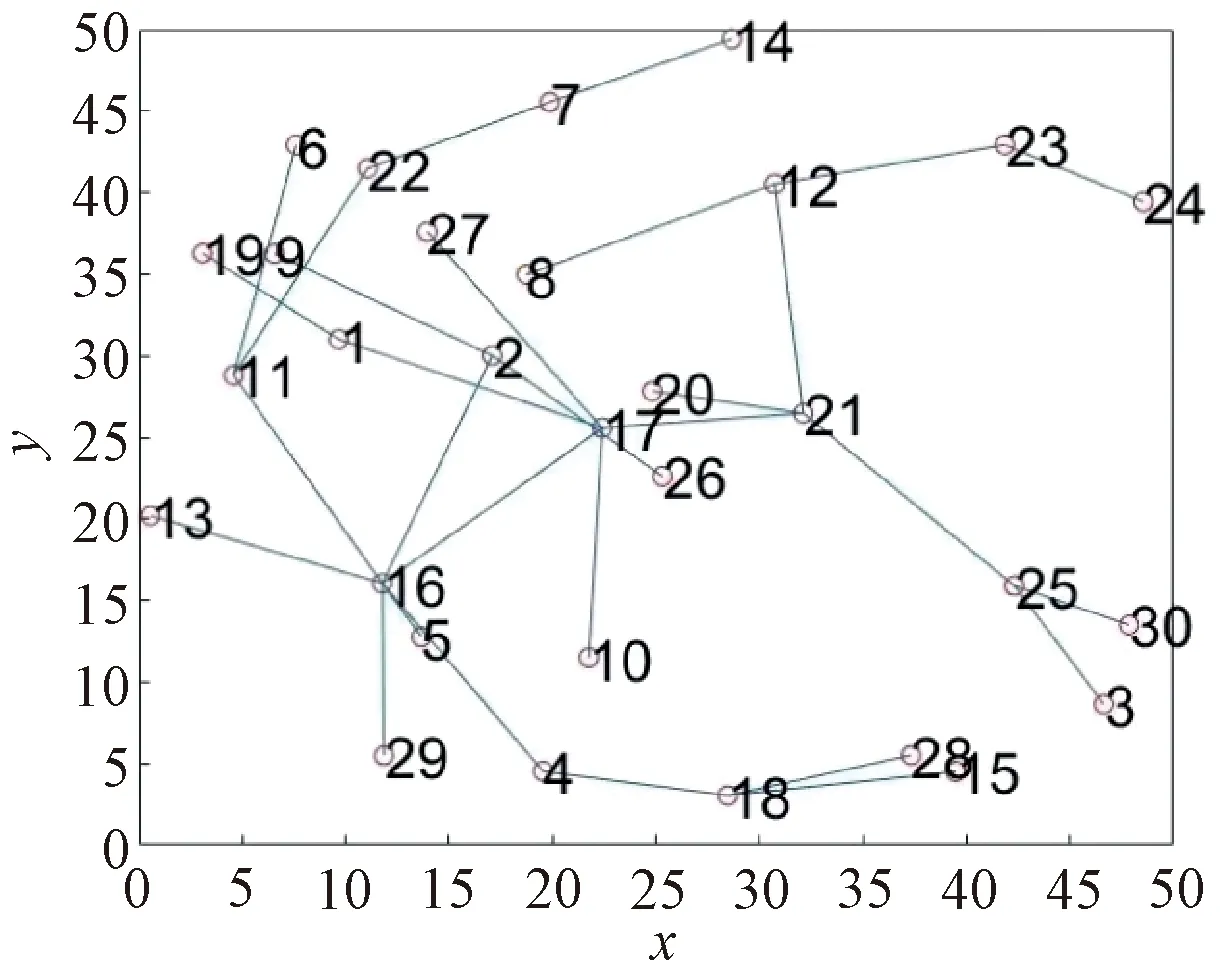
图9 最小化通信链路后的拓扑结构图

4 仿真试验

为了验证最小化通信链路优化算法的有效性，基于MATLAB/Simulink软件环境搭建如图10所示的微电网系统。在图10所示的微电网系统中，5个相同容量的逆变型分布式电源DG1～DG5和两个负载Zload1、Zload2连接在同一公共母线上，其中母线侧电压为750 V，微电网侧电压为380 V，有功-频率下垂系数m=1×10-4Hz/kW,无功-电压下垂系数n=3×10-3V/var,一致性算法的比例系数为0.2，积分系数为0.3，Pload1=6 kW，Qload1=5 kvar，Pload2=8 kW，Qload2=6 kvar。线路阻抗ZL1=(0.000 1+j0.002)Ω，ZL2=(0.000 2+j0.004)Ω，ZL3=(0.000 3+j0.006)Ω，ZL4=(0.000 4+j0.008)Ω，ZL5=(0.000 5+j0.010)Ω。

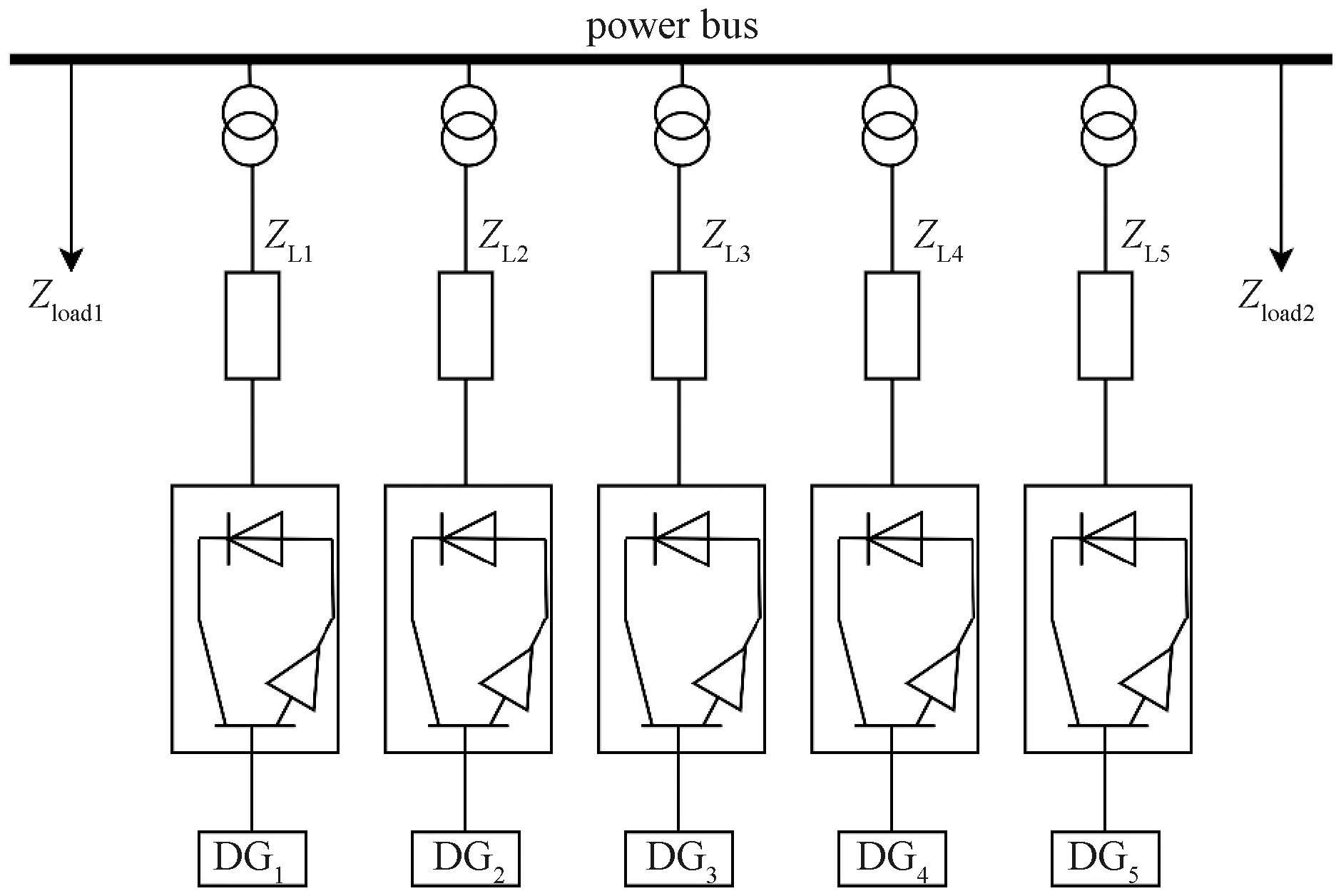
图10 微电网系统结构图

微电网的初始通信网络拓扑结构以及经最小化通信链路算法优化后的拓扑结构如图11所示。由图11可知，代数连通度均为1，通信链路由6条减少为4条。由此可见，不仅代数连通度没有减小，系统的收敛速度也与原来保持一致，并且通信成本在原来的基础上降低了1/3。

图11 微电网通信网络拓扑图

微电网在0～0.3 s处于下垂控制，在0.3 s时加入一致性算法，各个分布式电源输出的无功功率如图12所示。由图12可知，在优化后的拓扑结构的基础上，无功功率在3.5 s左右实现了一致性收敛，完成了无功功率均分。

5 结 语

针对微电网中分布式电源间通信，研究拓扑结构影响收敛速度和通信成本的问题。根据图论和分布式一致性理论的原理，在全连通图的条件下使系统能够达到收敛状态；再根据灵敏度和梯度下降思想，设计了一种最小化通信链路算法，在系统的代数连通度减小量最小的前提下，删除了部分通信链路，使得通信成本明显降低。仿真结果表明，经最小化通信链路算法优化后的系统依然能够实现无功功率均分，充分验证了最小化通信链路算法的有效性。提出的算法在一定程度上证明了删除通信拓扑结构的某些边可以使代数连通度的影响趋于最小化，并且可以明显降低通信成本。