基于两层次低秩分解的无监督织物疵点检测方法

邓智超， 邓开连， 张 磊， 刘肖燕， 燕 帅

(东华大学 信息科学与技术学院， 上海 201620)

织物疵点检测是纺织品质量控制过程中的关键环节之一。目前，大多数织物检验方法采用高成本的人工检测，需要大量人工标注信息。因此，探索一种泛化性好、疵点定位精度高和疵点类别分辨能力强的无监督织物疵点检测方法，具有重要的学术价值和应用价值。

近年来，针对织物疵点的检测算法主要包含4种方法。一是基于统计的方法，主要包括直方图统计[1]、共生矩阵[2]、显著图重构[3]等。虽然这类方法计算量小, 但是对环境条件敏感, 错检、漏检率较高。二是基于频谱的方法，主要包括傅里叶变换[4]、小波变换[5]、Gabor 滤波器[6-7]等。基于傅里叶变换的方法无法定位疵点位置，而小波变换和Gabor 变换的计算成本高, 难以用于生产过程中的实时检测。三是基于模型的方法，主要包括高斯混合模型[8-9]、马尔科夫随机场模型[10]等。基于模型的方法稳健性较差，实际应用的效果不佳, 近几年对其研究较少。四是基于机器学习[11-12]的方法，常见的有自动编码器[13-14]、卷积神经网[15-17]、对抗网络[18-19]等。由于不同面料的纹理背景、环境光线强弱和干扰噪声的影响，面料疵点背景会有很大的差异，这使得基于机器学习的方法难以提取缺陷特征，因此实际操作中为保证检测精度，针对不同面料需花费巨大成本训练专有检测模型。由于面料疵点种类繁多、形态多样，监督学习在多形态疵点下，人工标注数据费时费力，难以对缺陷特征进行充分学习，尤其在实际操作中，未知的、新的疵点不断出现，监督学习很难实现高精度的检测。

综合以上分析可知，现有基于机器学习的检测方法很难利用大量无标注信息，且对不同纹理的适应性不强，致使检测效果不明显。针对织物组织纹理结构复杂、花型繁多、材质多样的特点以及生产过程中环境的影响，如何提高无监督检测模型的泛化能力、疵点定位精度和疵点类别分辨能力仍然是研究的热点。

提出基于两层次低秩分解的无监督织物疵点检测方法：首先，利用噪声、背景底纹、疵点信息的低秩和稀疏特性，建立两层次低秩分解模型，通过交替方向乘子法对模型求解，实现疵点和背景噪声的分离，提高算法对不同纹理织物、光线强弱和面料歪斜的适应性；其次，利用检测框邻域图像隶属度的相似性与层次聚类的递进性，通过设计深度聚类网络的联合训练方式，提高疵点定位精度，极大地缓解因数据复杂导致深度聚类网络训练难以拟合的问题。

1 无监督织物疵点检测方法

针对疵点数据背景复杂、干扰噪声多的问题，提出了基于两层次低秩分解的无监督织物疵点检测方法，该方法流程如图1所示。

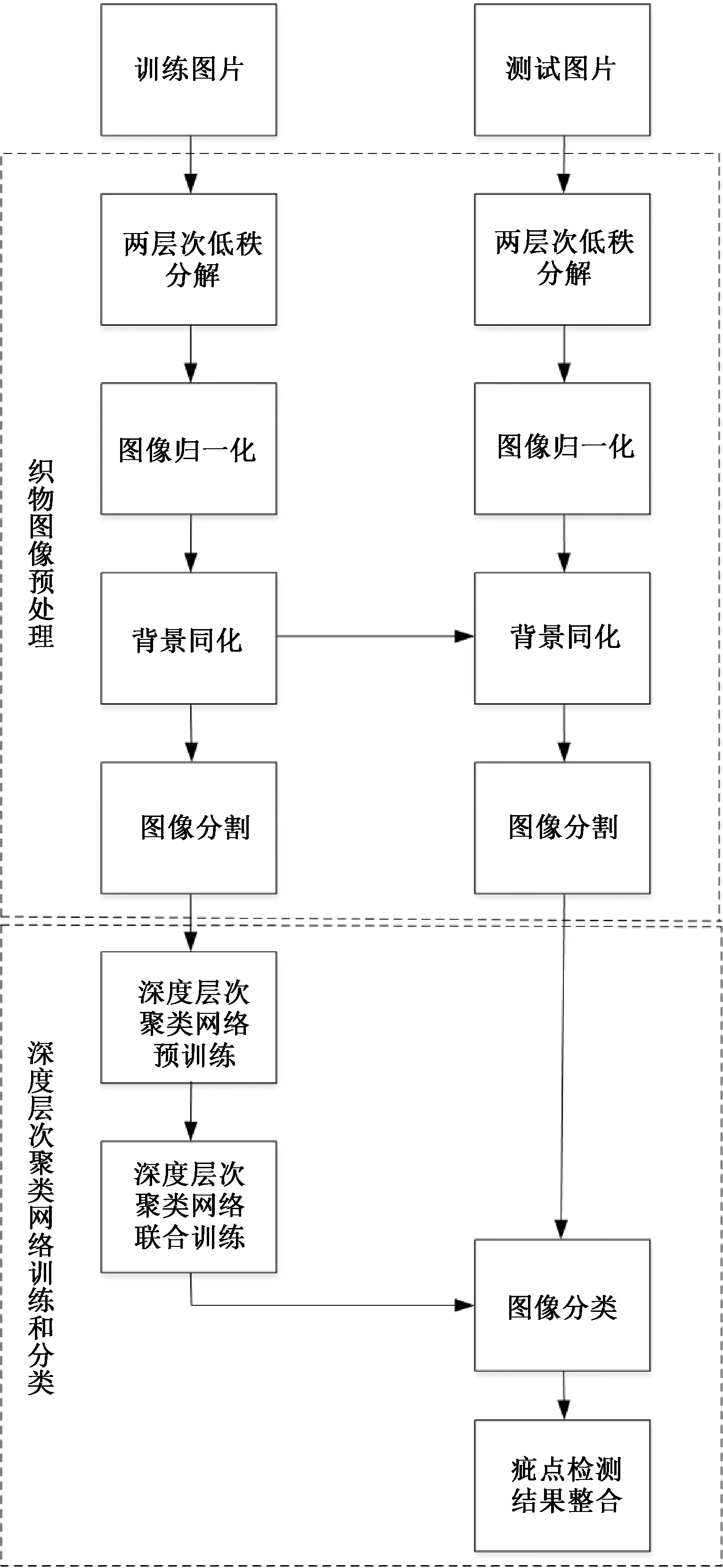
图1 基于两层次低秩分解的无监督织物疵点检测方法流程图

由图1可知，无监督织物疵点检测分为图像预处理和深度层次聚类网络两部分。图像预处理部分：首先，利用背景底纹复杂性和疵点信息的低秩、稀疏特性，进行两层次低秩稀疏阵分解，将面料的疵点信息与背景和噪声分离，减轻外界的影响。其次，调整训练，集中每张图像各通道的像素范围至该通道像素极限范围，以进行图像归一化。再次，统计训练集中所有图像各通道的像素均值，并调整训练集所有图像各通道的像素均值为对应通道统计均值，实现训练集图像的背景同化，提高检测模型的泛化能力。最后，将处理后尺寸为M×N的图像分割成(M-m-1)×(N-n-1)个尺寸为m×n的小图像，并送入深度层次聚类网络训练。深度层次聚类网络部分：首先，通过对编码器进行预训练，初始化编码器。其次，利用疵点邻域图像的隶属度具有相似性的特点，对网络层次聚类进行联合训练，缓解数据复杂导致网络难以拟合的问题，提高疵点定位精度和类别辨识的准确率。最后，通过合并相同类别且重合的疵点检测小框，根据所包含疵点检测小框的数量，对重合度过高的疵点大框进行非极大抑制，完成疵点的无监督目标检测。

1.1 织物图像预处理

1.1.1 两层次低秩分解

针对模型检测精度因面料背景的差异性而有所降低的问题，利用背景、噪声、疵点的低秩和稀疏特性，建立了如式(1)所示的两层次低秩分解模型。第一层次从原始图像中分解出背景矩阵L1和疵点与噪声的混合矩阵S1；第二层次从疵点与噪声的混合矩阵中分解出疵点矩阵L2和噪声矩阵S2。通过交替方向乘子算法，对两层次低秩分解模型求取最优解，从而实现疵点与噪声和背景的分离。

(1)

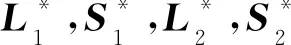
求解式(1)属于NP-hard问题，难以获得全局最优解，因此将其转换为凸优化问题的求解：

λ1‖S1‖1+‖L2‖*+λ2‖S2‖1)

(2)

式中：‖‖*表示核范数；‖‖1表示1范数。

(3)

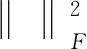
最后利用交替方向乘子算法[20]进行两层次的迭代求解：

(4)

(5)

(6)

(7)

Y1k+1=Y1k+μ1(F-S1k-L1k)

(8)

Y2k+1=Y2k+μ2(S2k-S2k-L2k)

(9)

式中：k为迭代轮次。

1.1.2 图像归一化

将低秩稀疏阵分解后的图像归一化到0～255级灰度。

(10)

式中：Di为归一化后的疵点i通道的像素矩阵；L2i为低秩稀疏阵分解后的图像L2的第i通道像素矩阵。

1.1.3 背景同化

针对图像经过归一化后背景不一致的问题，统计所有图像各通道的像素均值,并调整所有图像各通道的像素均值为各通道统计均值。

(11)

式中：nimg为数据集中的图像数量；M×N为图像尺寸；A为所有元素为1的矩阵；Dijk为第k张图像第i个通道的第j个像素值。

1.2 深度层次聚类网络

1.2.1 深度层次聚类网络的结构

针对监督学习在多形态疵点下难以实现高精度检测的缺点，本文设计了深度层次聚类网络，整个网络由卷积编码器、嵌入层和聚类层3部分组成。深度层次聚类网络结构如图2所示。

由图2可知，其中聚类层使用K-means作为聚类算法，其将相同类别并且重合的疵点检测小框合并成疵点检测大框，并对重合度过高的疵点大框以所包含疵点检测小框的数量进行非极大抑制。深度层次聚类网络参数如表1所示。

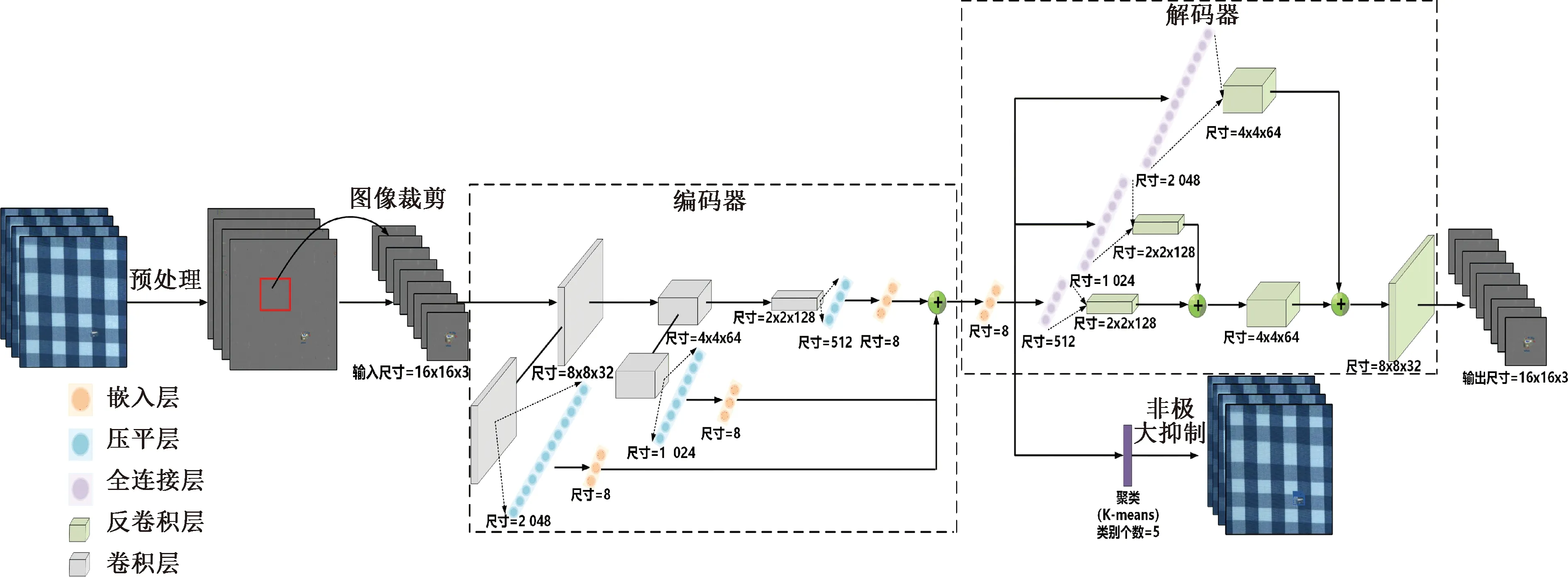
图2 深度聚类网络结构图

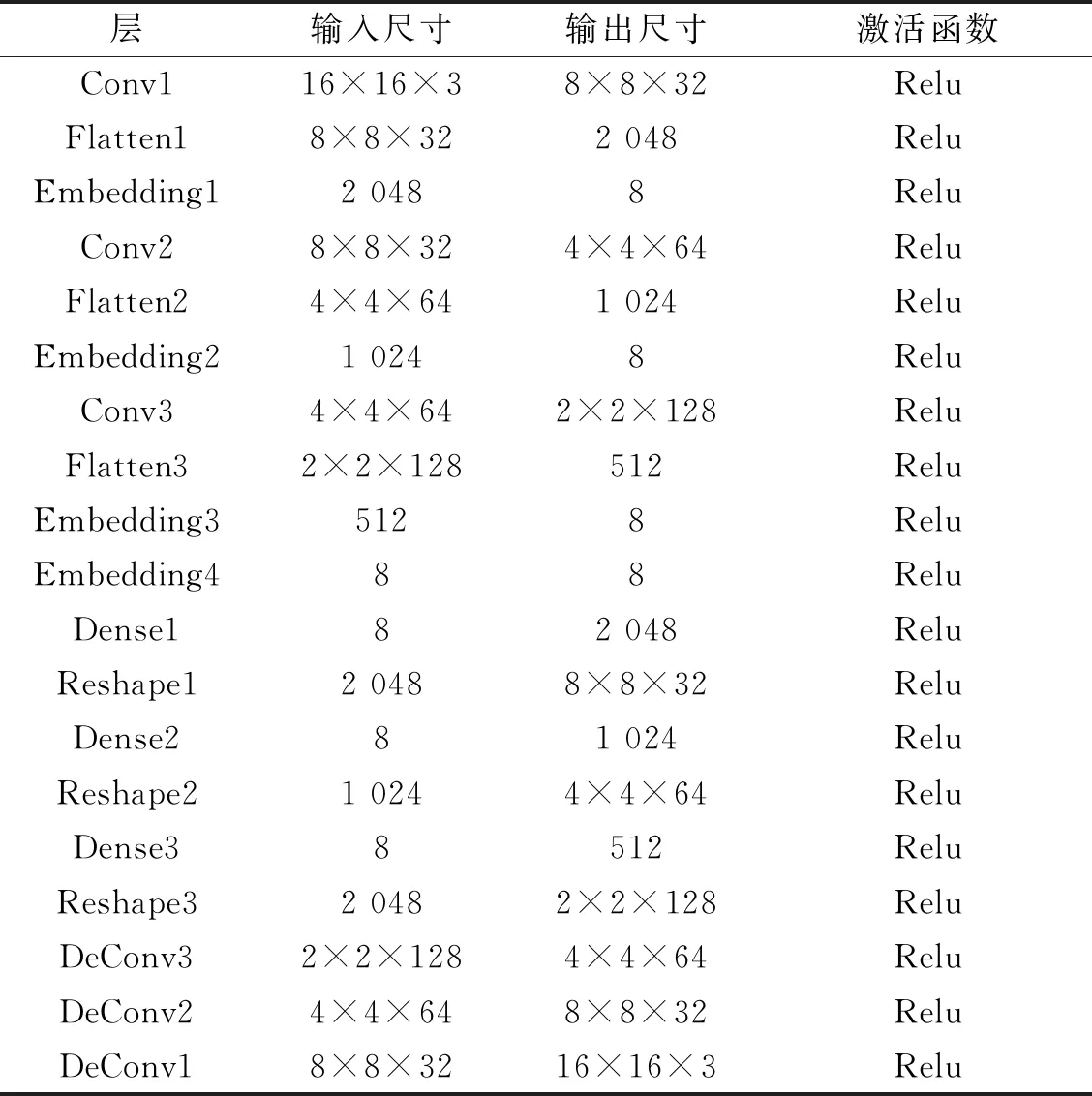
表1 深度层次聚类网络参数

1.2.2 深度层次聚类网络的预训练

对编码器进行预训练，从而初始化网络参数。其损失函数LAE为

(12)

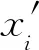
1.2.3 深度层次聚类网络的聚类损失函数

利用DEC(deep embedded clustering)[21]中定义聚类损失的思想和检测框邻域的相似性的特点，定义软标签分布和目标分布之间的KL(Kullback-Leibler)散度为聚类损失。

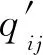
(13)

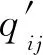
根据每张图像的邻域图像的隶属度对原隶属度进行修正，如式(14)～(16)所示。

(14)

dk=max(|x-s|,|y-t|)

(15)

(16)

式中：hij为未进行归一化的qij；Nnb为所用的邻域点的个数;dk为像素点之间的棋盘距离；qij为zi到第j类的基于邻域的隶属度。

(2)目标分布。保证聚类目标能使数据分布更加接近聚类中心，因此定义聚类目标分布pij，如式(17)所示。

(17)

式中：pij为zi到第j类的目标隶属度。

(3)聚类损失函数。聚类损失值计算如式(18)所示。

(18)

式中：Lc为聚类损失值。

1.2.4 深度层次聚类网络的联合训练

为保证聚类训练过程中嵌入层提取的低维数据特征能够表示原图像而不畸变，借助DCEC(deep convolutional embedded clustering)[22]的训练思想，通过同时降低LAE和Lc对深度层次聚类网络进行联合训练，因此联合训练损失函数如式(19)所示。

Ljoint=Lc+αLAE

(19)

由于面料疵点种类繁多的特点，直接对深度层次聚类网络进行联合训练可能无法拟合，因此联合训练中使用了类似层次聚类的方式进行训练，训练的流程如图3所示。

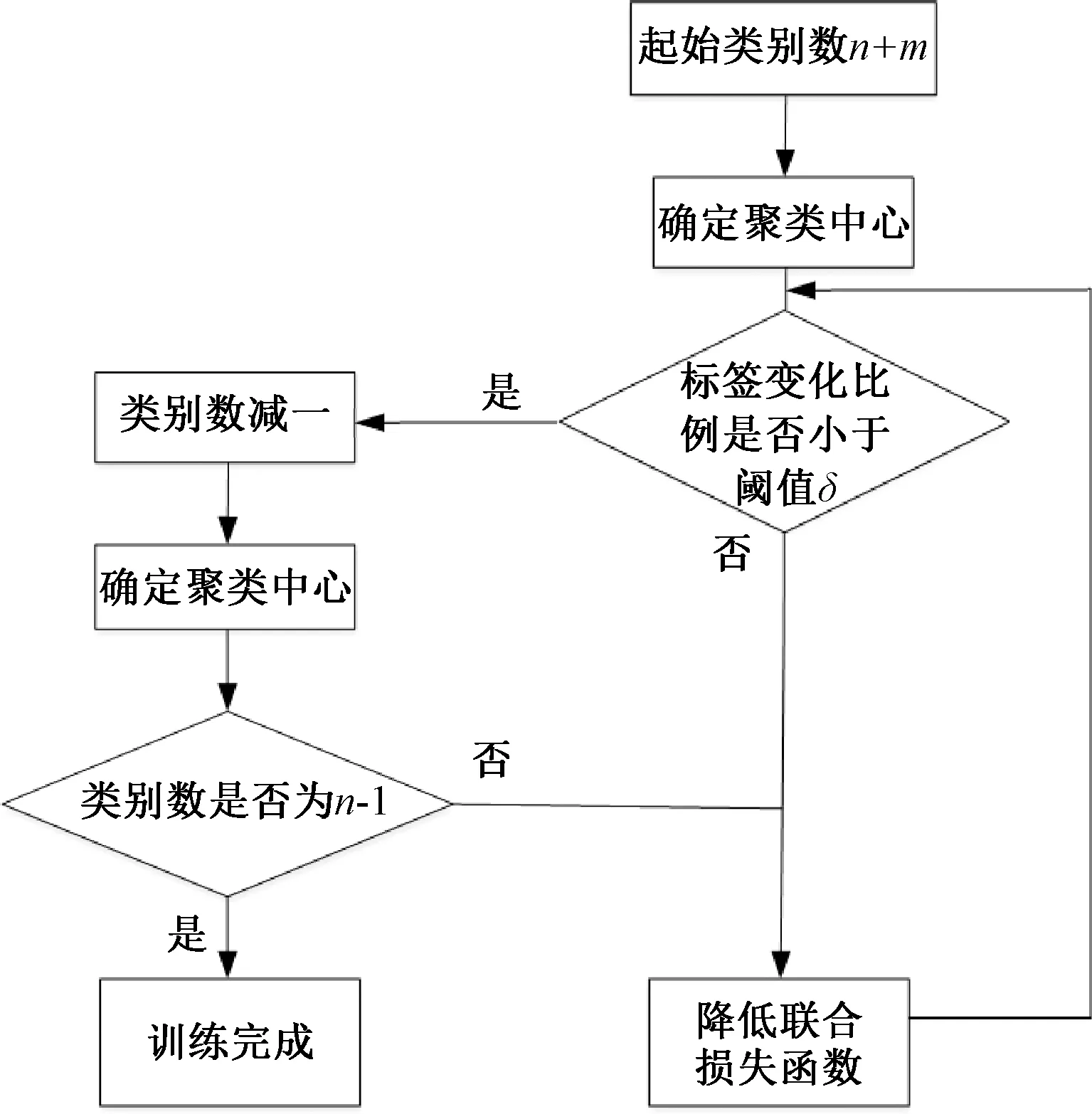
图3 联合训练的流程图

由图3可知，聚类类别会从高于最终类别数的n+m降低到最终的类别数n。初始聚类类别数为n+m，确定聚类中心，然后降低联合训练损失值，当达到类别降低的条件时，即标签变化的比例小于设定的阈值δ时，将类别数减一，再次确定聚类中心。以此类推直到最终降低到n个种类且达到类别降低条件，此时，深度层次聚类网络的训练完成。

2 研究结果与分析

试验平台软件部分使用Python 3.6和Tensorflow 2.0搭建深度学习模型，在GPU为NVIDIA TESLA T4的服务器上完成检测模型的训练与测试。

试验分为两个部分：(1)通过层次聚类网络的聚类能力试验，检验层次聚类网络的聚类能力；(2)通过模型进行织物疵点检测试验，检验两层次低秩分解和深度层次聚类网络对于面料疵点测检的有效性和算法泛化性。

2.1 聚类能力对比试验

2.1.1 数据集

层次聚类网络的聚类能力试验在4个数据集上进行评估。

MNIST-full：MNIST数据集是由总计70 000个28像素×28像素的手写数字组成。

USPS：USPS数据集包含9 298幅16像素×16像素的灰度手写数字图像。

Fashion-MNIST：Fashion-MNIST数据集包含了10个类别的70 000张28像素×28像素的时尚产品图像。

COIL-20 ：COIL-20 数据集包含了20个类别的1 440张128像素×128像素物体图像。

2.1.2 试验结果

将本文深度聚类网络与文献[21-25]深度聚类网络算法(K-means、DEC、DCEC、MDEC(multi-view deep embedded clustering)、DMJC(deep multi-view joint clustering)、VAED(variational autoencoder with distance))进行对比，测试深度聚类网络的聚类精度，选用准确率Aclustering和归一化互信息NNMI[26]作为网络聚类能力的评价指标,其计算分别如式(20)和(21)所示。

(20)

式中：ms为样本个数；li为真实标签；ci为聚类预测标签。真实标签与聚类预测标签的对应关系通过匈牙利算法计算获得。

(21)

式中：MMI(l,c)为l与c的互信息；l为真实标签的集合；c为聚类预测标签的集合；H为熵。

由聚类算法的对比试验结果(见表2)可知，相较于改进之前的DEC和DCEC网络，本文算法有了明显的进步，并且在大部分数据集上的聚类能力优于现有算法。

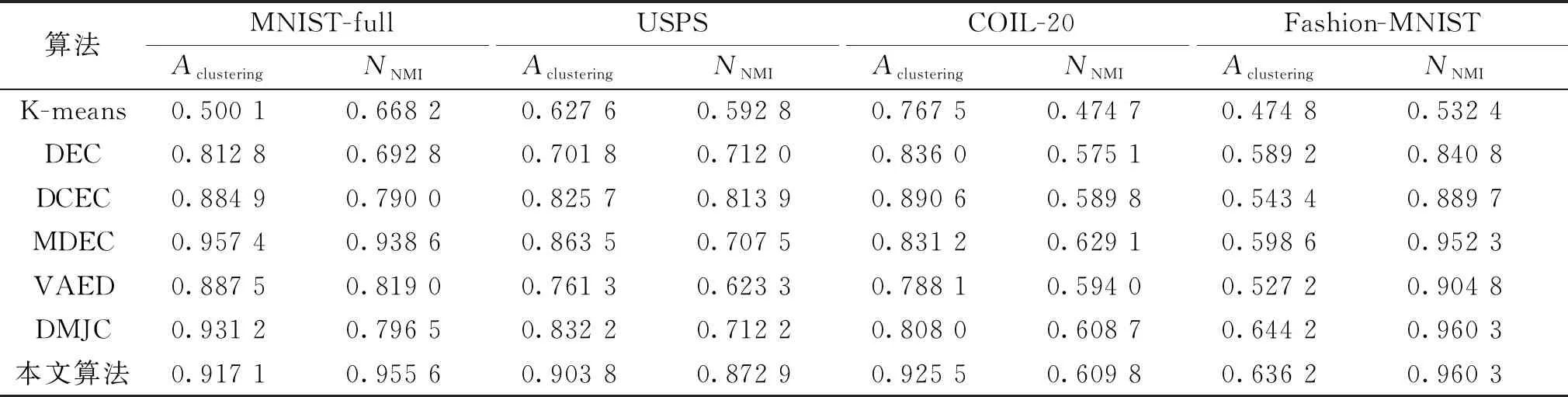
表2 聚类算法准确率与归一化互信息对比

2.2 疵点检测对比试验

2.2.1 数据集

织物疵点检测试验选用上海嘉麟杰的典型格纹面料和典型针织棉麻面料以及TILDA中的星纹面料和点纹面料作为试验样本，自行设计搭建面料疵点检测设备。面料疵点试验平台硬件参数如表3所示。

表3 面料疵点试验平台硬件参数

样本疵点类型为生产中经常出现的缺经、缺纬、渍类和破洞等4类。格纹面料数据一共包括623张512像素×512像素的图像，其中缺经143张、缺纬134张、渍类87张、破洞159张、正常100张。针织棉麻面料数据集一共包括465张512像素×512像素的图像，其中缺经96张、缺纬104张、渍类109张、破洞106张、正常50张。TILDA中的星纹面料共包括25张疵点图像和25张正常图像。TILDA中的点纹面料共包括110张正常图像和120张疵点图像。

2.2.2 试验结果

利用格纹面料训练的模型对4种面料进行检测，将本文算法与其他无监督算法(DEC、DCEC、MDEC、DMJC、VAED)和监督算法[27-29](Faster R-CNN、Yolov3、SSD)进行检测精度对比，分析两层次低秩分解(TLRD)和深度层次聚类网络对织物疵点检测精度的影响。试验以检测模型的精度为评价指标，精度计算如式(22)所示。

(22)

式中：TP为真正例；FN为假反例；FP为假正例；TN为真反例；Adetection为检测模型的精度。

疵点检测精度试验结果对比如表4所示。

表4 不同算法对不同面料疵点的检测精度试验结果对比

由表4可知，两层次低秩分解的无监督织物疵点检测方法在格纹数据上训练的模型，不仅格纹织物疵点的检测精度能达到81.5%，而且平纹、点纹和星纹织物疵点的检测精度也能分别达到86.1%、91.7%和95.2%。两层次低秩分解模型(TLRD)与单层次低秩分解模型(LRD)相比，对于现有无监督算法,TLRD大都能有效提高其疵点检测精度，提高检测模型的泛化能力。与无监督算法DEC、DCEC、MDEC、VAED、DMJC相比，基于邻域的深度层次聚类网络算法能更准确地对织物疵点进行检测，而且模型具有更好的泛化能力。与监督学习算法SSD、Faster-RCNN、Yolov3相比，本文算法对于格纹面料的检测精度高于SSD，但由于没有使用标签数据，低于Faster-RCNN、Yolov3的检测精度，而对于其他3种面料的检测精度都高于监督算法，因此本算法具有更好的模型泛化能力。

2.3 面料疵点检测结果

将4种不同面料的疵点图像输入检测模型，得到疵点定位与分类的检测结果。针织格纹面料、机织棉麻平纹面料、星纹面料、点纹面料的疵点检测结果分别如图4～7所示。检测结果包括疵点种类和边界框，每种颜色的疵点边界框对应不同种类的疵点。检测结果表明，检测图像经过两层次低秩分解等预处理后，能够将不同面料的不同纹理背景转化为相同背景，以突出疵点的位置。因此,本算法不仅能够对已训练过的格纹面料进行精准的疵点分类与定位，而且对于未训练的平纹、星纹、点纹面料，也能进行精准的疵点分类与定位。在实际面料疵点检测中，能够极大地减少标记成本和训练不同面料疵点检测的专有模型的成本。

图4 格纹面料疵点检测

图5 平纹面料疵点检测

图6 星纹面料疵点检测

图7 点纹面料疵点检测

3 结 语

本文提出一种基于两层次低秩分解的无监督织物疵点检测方法，实现了对针织格纹面料的4类疵点的有效检测，检测精度为81.5%。同时在使用相同的模型下对平纹、点纹和星纹面料疵点检测的精度也能分别达到86.1%、91.7%和95.2%，有利于解决当前面料疵点检测算法泛化性差、难以适应面料种类动态变化的生产实际问题。