基于改进粒子群算法的凿岩机械臂轨迹规划

黄开启，陈翀，刘展飞

（江西理工大学电气工程与自动化学院，江西 赣州 341000）

为了解决在施工中的作业环境差、耗资耗时多、劳动强度大等问题，早在20世纪70年代就开始研究凿岩设备代替人工作业，现如今凿岩机器人的应用更加普遍，为了使凿岩机器人更适合复杂高精度的作业，提出了一种7自由度凿岩机器人，随着冗余度的增多，高性能的轨迹规划成为了机器人领域研究重点之一。

机械臂的轨迹规划方法很多，多项式插值因为其计算简单的优点而被广泛使用。孙玥等［1］为了解决机械臂在运动过程中速度和加速度的突变带来的抖动和不稳定等问题，采用了5次多项式插值对机械臂的轨迹拟合，确保机械臂运行平稳；方爽［2］等采用7次多项式插值方法有效地解决了加加速度不连续问题。但随着多项式插值次数的增加，凸包性质不够好，计算难度也越来越大，不少学者采用了分段插值方法。Guan等［3］提出了一种结合3阶和4阶多项式进行轨迹插值的方法，对轨迹的第一段和最后一段使用两个4次多项式，对其他段使用3次多项式；梁志鹏等［4］提出了一种4-4-4-4-5插值轨迹规划方法，分段方法能够较好地解决高次插值计算量大的问题，降低了“龙格现象”的发生。以上研究虽然解决了传统算法难以优化高阶多项式的问题，但没有考虑多项式插值轨迹最优问题，粒子群算法［5-7］在优化问题中得到广泛使用。

本文提出了一种在速度和加速度约束下，利用改进粒子群算法以时间为目标函数，对分段多项式插值进行优化的轨迹规划算法。以7自由度凿岩机械臂为研究对象，在机械臂运动学分析的基础上确定多项式插值函数。在满足约束条件下，以时间最短为目的，对3-5-3分段多项式插值的各时间段进行优化。对轨迹规划的插补时间引入智能算法优化，能够减少机械臂运动时间，降低机械臂运动能耗，并且能够有效地避免机械臂不必要的冲击，增加了稳定性。

1 机械臂运动学分析

运动学分析是轨迹规划的基础。机械臂在运动时，通过末端位姿可以获取各关节的位置变化，从而达到指定位姿。本文研究凿岩机器人各关节按照［8-9］的规则建立D-H模型，如图1所示，D-H参数表如表1所示。表中：αi-1为扭转角；ai-1为杆件长度；θi为关节角；di为偏移距。

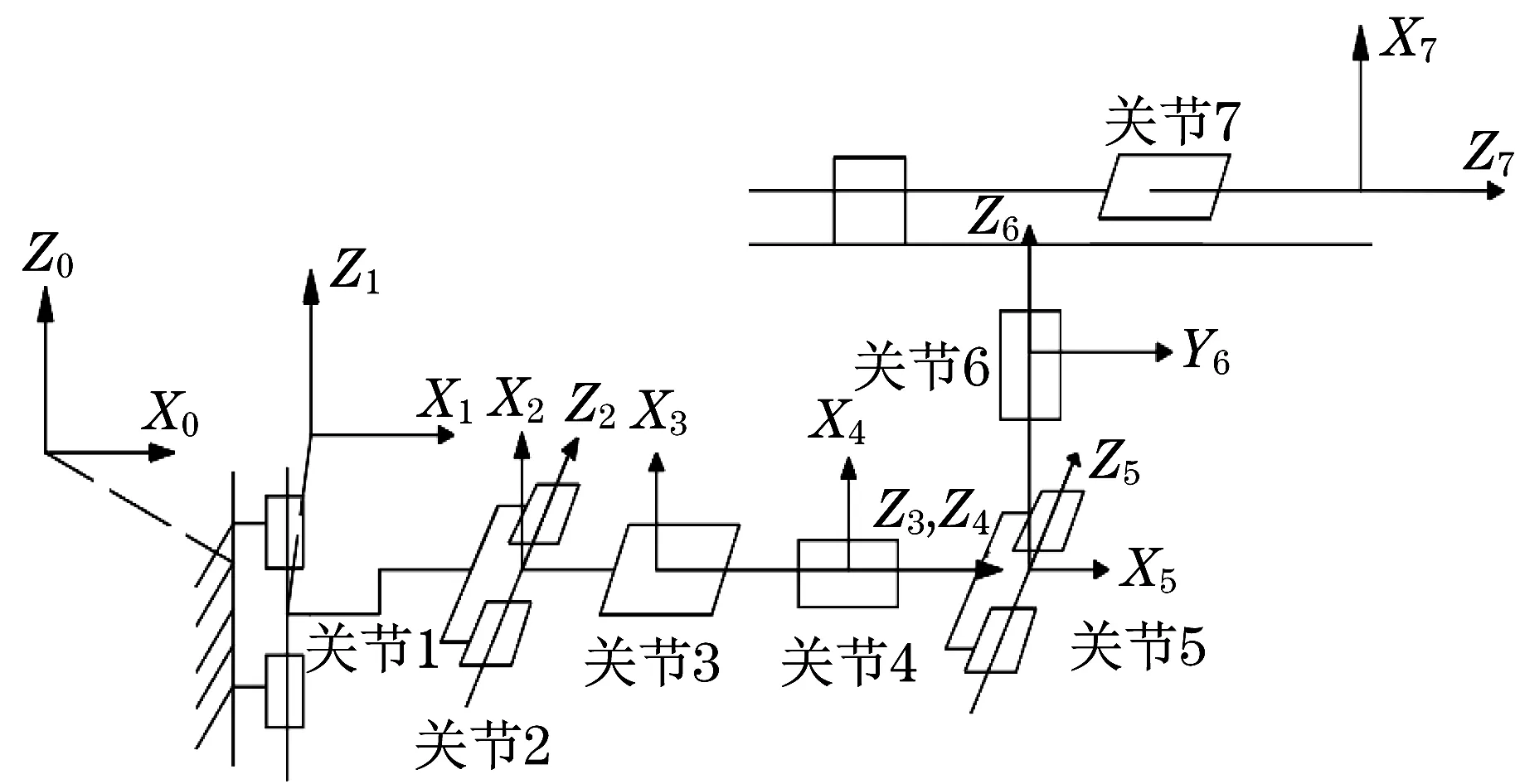
图1 机械臂坐标系Fig.1 Robotic arm coordinate system

表1 机械臂的D-H参数Tab.1 D-H parameters of the manipulator

机械臂第i个和第i-1个连杆之间的变换矩阵为

根据前面给定的D-H参数表，代入公式可以得到每个连杆之间的变换矩阵01T、12T、23T、34T、45T、56T、67T，为了得到基座与末端执行器之间的关系，将各连杆的变换矩阵相乘，得到机械臂的末端位姿矩阵为

式中：向量n、o、a分别为机械臂末端执行机构的法向矢量、滑动矢量和接近矢量；向量p为机械臂的位置矢量。

机械臂的运动学逆解可以由文献［10］所得。

2 多项式插值函数的构造

三次插值多项式因为计算简单而广泛应用于轨迹规划，但由于机械臂运行时稳定性较差，可能存在关节磨损，不利于控制精度。本文提出了一种3-5-3分段多项式插值方法，在起点和终点中插入两个中间点，在第1段和第3段使用三次多项式插值，第2段使用5次多项式插值，这样既能保证轨迹的光滑度又能避免因为次数过高而引起的计算复杂。

本研究采用的3-5-3多项式插值方法为

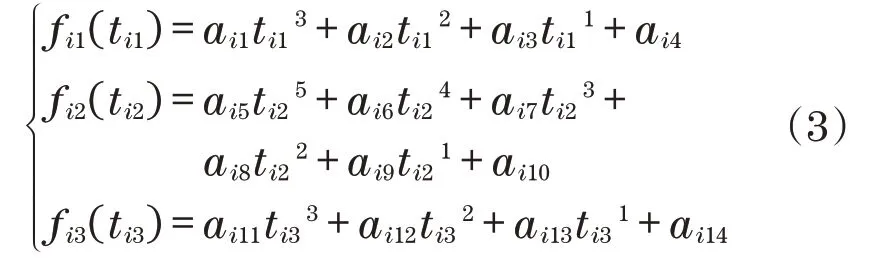
式中：aim为第i个关节中第m个未知系数；i=1，2，…，n，n为关节数；m=1，2，…，14；fi1(ti1)、fi2(ti2)、fi3(ti3)为第i个关节对应的第1、第2、第3个区间中的位置；ti1、ti2、ti3为第i个关节对应的第1、第2、第3个区间中的时间。

为保证轨迹的光滑性，在起点、终点和2个中间点已知的情况下，假设起点速度、加速度、终点速度、加速度都为零；中间两点位置、速度、加速度均连续，在此假设下可由以下公式计算未知系数：

式中：T为关于第i个关节的插补时间ti1、ti2、ti3的矩阵；A1～A8为矩阵T中对应的分块矩阵；Q为关节角的位置矩阵；A为系数矩阵。

3 目标函数的选取

根据机械臂运动约束和工业需求，机械臂运动时，在保证关节平滑运行时，关节i允许的最大速度为vmaxi(°)/s，最大加速度为amaxi（°）/s2。本文优化的目的是在3-5-3多项式插值的基础上提高机械手的效率和稳定性，分别对每个关节进行优化，将第i个关节经过的4个点分成对应的3个时间段，在约束下对时间进行优化，因此以最短的运行时间作为适应度函数为

约束条件为

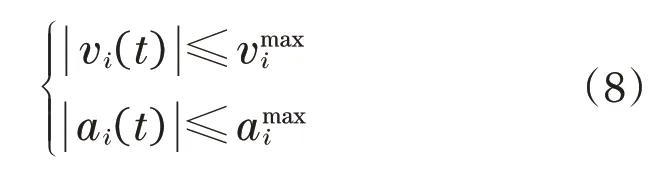
4 改进的粒子群算法

粒子群算法（particle swarm optimization，PSO）最早是在1995年由Eberhard和Kennedy［11］共同提出，其主要思想来源于早期对很多鸟类的群体行为的建模与仿真。设Zj=(zj1，zj2，…，zjD)为第j个粒子的D维位置矢量，代入到根据要求设定的适应值函数f(t)计算Zj当前的适应值，即可衡量粒子位置的优劣；Vj=(vj1，vj2，…，vjd，…，vjD)为粒子j的飞行速度，即粒子移动的距离；Pj=(pj1，pj2，…，pjd，…，pjD）为粒子迄今为止搜索到的最优位置；Pg=(pg1，pg2，…，pgd，…，pgD)为所有粒子到目前为止搜索到的最优位置。

在每次迭代中，粒子根据以下式子更新速度和位置：

式中：j=1，2，…，m，m为粒子数；d=1，2，…，D，D为粒子维度；k为迭代次数；r1、r2为［0，1］之间的随机数；ω为惯性权重；c1、c2为学习因子。

为了更好地到达全局最优位置，提出了一种自适应惯性权重和动态调整学习因子相结合的改进方法。种群的全局搜索能力由全局搜索速度和惯性控制。如果ω得到一个固定的较大值，算法的收敛速度会过慢，最终解的精度也会很低。如果ω得到一个固定的较小值，算法可以检测到局部区域，在这种情况算法容易早熟收敛。此外，还发现PSO的惯性加权值不宜过高也不宜过低。在0.9～0.4之间降低效果最好。更新后的惯性权重规则为

式中：ωn为ω的最大值；ωx为ω的最小值；Tx为最大迭代次数；k为当前迭代次数。

为了增强算法前期粒子的搜索能力和后期的收敛能力，本文在前期保持较大的c1值和较小的c2值，在算法的后期保持c1值较小，c2值较大。文献［12］中推导可知，要满足PSO算法的收敛条件，算法各参数需要满足以下条件：

更新后的学习因子规则为

粒子群优化算法的流程图如图2所示。

图2 流程Fig.2 Flowchart

5 仿真验证与结果分析

本例中的运行环境为Windows10 64位，处理器为Intel（R）Core（TM）i5-7300HQ CPU@2.50GHz，RAM 8GB，软件Matlab。

在工作范围内，取机械臂末端4个位姿，分别表示初始点、中间点1、中间点2和终点。表2中前3个值是位置信息，后3个值是姿态信息。利用文献［10］的运动学逆解方法，将笛卡尔空间中的插值点转换为关节空间中的插值点，转换后见表3。

表2 机械臂末端位置和姿态信息Tab.2 Information of robotic arm terminal position and posture

表3 关节角度的插值点Tab.3 Interpolation points of joint angles

当起始点和终点的速度和加速度均为零，且中间点1和中间点2速度、加速度连续时，设每段插补时间为5 s，用传统的3-5-3多项式插值法可以得到优化前的各关节运动的位置、速度、加速度曲线，此时运行效率低下。

采用改进的粒子群算法求解具有速度、加速度约束的多项式插值的最优时间。以关节1最优时间的求解为例，关节1各节段的时间进化如图3所示。参数设置：初始种群设置为50；最大迭代次数为100次；最大速度为25（°）/s；最大加速度为15（°）/s2；ωn=0.9；ωx=0.4。综合考虑安全、稳定、效率等因素，给每个关节设置合适的速度、加速度。利用改进的粒子群算法优化得到其他关节各节段的最优时间，结果见表4。

图3 关节1各段时间进化Fig.3 Time evolution diagram of joint 1

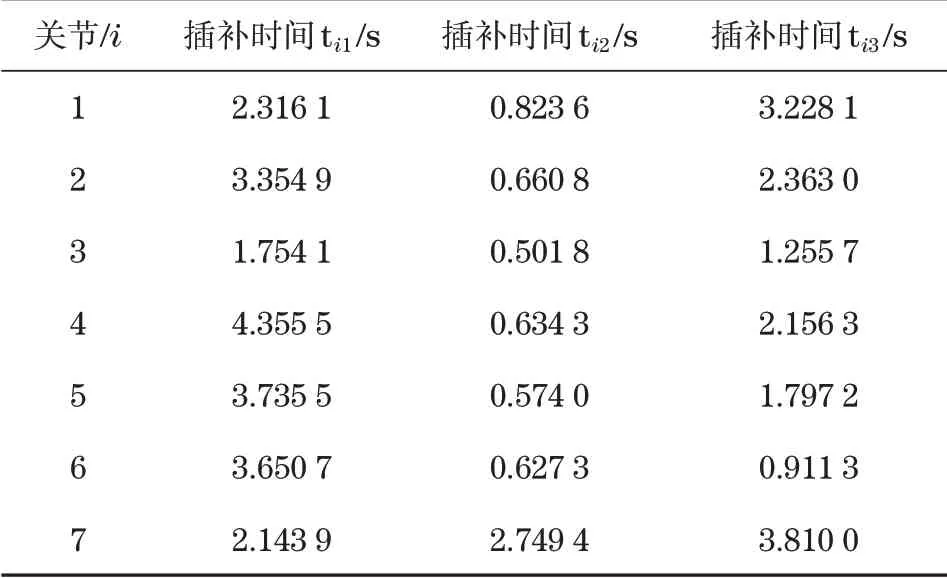
表4 各个关节的最优时间Tab.4 Optimal time for each joint

因为机械臂各个关节的运动是同步的，所以每个时间段都选取各关节中的最大时间来作为每个分段的 插 补 时 间。由 表4可 知：Max（ti1）=4.355 5 s，Max（ti2）=2.749 4 s，Max（ti3）=3.810 0 s。与未优化前相比，插值时间缩短了4.085 1 s。

图4～图6为改进粒子群算法优化后得到的位置、速度、加速度曲线。由图可以看出，优化后的速度、加速度有所增加，但没有突破极限并且趋向于极限，仍然满足约束条件。

图4 优化后的各关节位置曲线Fig.4 The optimized position curve of each joint

图6 优化后的各关节加速度曲线Fig.6 The optimized acceleration curves of each joint

图5 优化后的各关节速度曲线Fig.5 The optimized velocity curves of each joint

6 结语

利用3-5-3分段多项式插值进行轨迹拟合，可以保证机械臂位置、速度、加速度连续，提高运行稳定性，但是每个分段的插补时间的不确定性，严重影响了机械臂工作的工作效率，提出了一种以速度和加速度为约束条件，基于改进粒子群算法的关节空间时间最优轨迹规划方法。仿真结果表明，改进粒子群算法具有更快的收敛速度和更好的优化结果。通过该算法优化后，机械臂各关节运行平稳，运行时间大大缩短，并且满足速度和加速度约束，能够较好地达到预期的优化效果。