挖掘机泵控负载敏感系统设计及结构参数优化

宋旋，刘志超

（1.黄河交通学院汽车工程学院，河南 郑州 454950；2.河南理工大学机械与动力工程学院，河南 焦作 454000）

挖掘机属于一类重型车辆，被广泛应用在综采工作面领域，可以实现成套设备的高效搬家过程［1］，能同时满足高效操作、灵活机动和低成本铲运多项要求。目前，挖掘机泵控多是以阀芯探测负载压力发生改变，再将结果传输至泵组控制系统中，之后泵组开始调节泵输出状态，确保输出压力与流量能够很好匹配负载，降低系统的损耗程度［2-4］；随着负载压力逐渐增大至某一特定值时，泵开始输出更小的流量，由此实现稳定的泵输出压力。但其存在面对负载复杂环境时运行不稳定的情况，因此，开发挖掘机泵控负载敏感系统尤为重要。

相关方面吸引了很多的研究学者，王敬国［5］研发了一种能够满足高效控制精度要求的负载敏感阀，显著改善了全液压钻机的阀控控制效果，也进一步优化了泵控技术，深入探讨了负载敏感阀故障影响因素并提出了改善方案；王晨升等［6］则利用泵对吊车液压结构进行了测试，依次分析了斜盘倾角、泵压力与流量的变化特征；马冲等［7］从理论层面进行分析并构建了相应的仿真模型，针对泵控制机构优化了阻尼孔与容腔的各项参数，实现了两者的高效匹配，同时以ADAMS与AMESim仿真；迪茹侠［8］对负载敏感系统进行了测试，对液压系统会受到较大冲击的情况，构建了相应的仿真模型；王亚军等［9］采用负载敏感技术设计得到了具备双向缓冲功能的液压缸，获得了一种新型结构的负载敏感制动阀。之后，对其进行测试发现，这种阀体结构可以与液压缸制动力以及负载惯性力形成良好匹配状态，尤其是可以满足连续制动的需求，与传统形式的溢流阀制动回路相比，能够实现液压缸运行过程的双向缓冲控制；朱帅等［10］采用液压蓄能器作为储能部件，同时设定了合适的变量泵排量，确保液压缸制动腔压力符合制动过程和对能量进行回收的条件，对该系统进行仿真发现，达到了优异的制动效果，实现高效回收能量的目标。

本文根据泵控负载敏感系统构建仿真模型，对负载敏感阀直径、旁路阻尼孔尺寸、弹簧刚度开展综合分析，构建得到泵输出流量与压力之间的函数关系，同时以AMEsim仿真平台验证了流量响应的性能。

1 负载敏感系统分析

1.1 负载敏感阀的结构及组成

执行元件的流量与压力的各个参数信号通过负载敏感阀传输至被控制量，因此，当负载改变后，被控制量也随之发生变化。以负载敏感系统实施制动时，系统能耗可以获得明显控制，有效克服缓冲腔压力造成的冲击影响，确保系统达到可靠运行的状态，实现系统运行寿命的延长，泵控负载敏感系统原理如图1。由图1可知，负载敏感阀组成部分包括电磁换向阀、单向阀、梭阀、负载敏感节流阀等多个结构。通常将这些结构与系统进油路按照并联的方式使用，对制动过程有着重要的影响。为实现负载的平稳制动，同时避免引起硬冲击现象，设计了具有螺旋外形的阀芯，使表面形成螺旋形的窄槽，从而减小流体压力。在进行制动的过程中，缓冲腔内形成的高压油，有一部分对负载敏感节流阀的左端产生作用，此时阀芯可以抵消弹簧弹力，作用实现往右运动的过程；还有一部分高压油流经节流阀的阀芯螺旋孔，使压力减小后再进入油箱内。随着高压油压力逐渐提高，阀芯发生了更明显的右移，需要流经更长的螺旋，使液压缸缓冲腔达到了更优背压，最终获得良好制动作用。

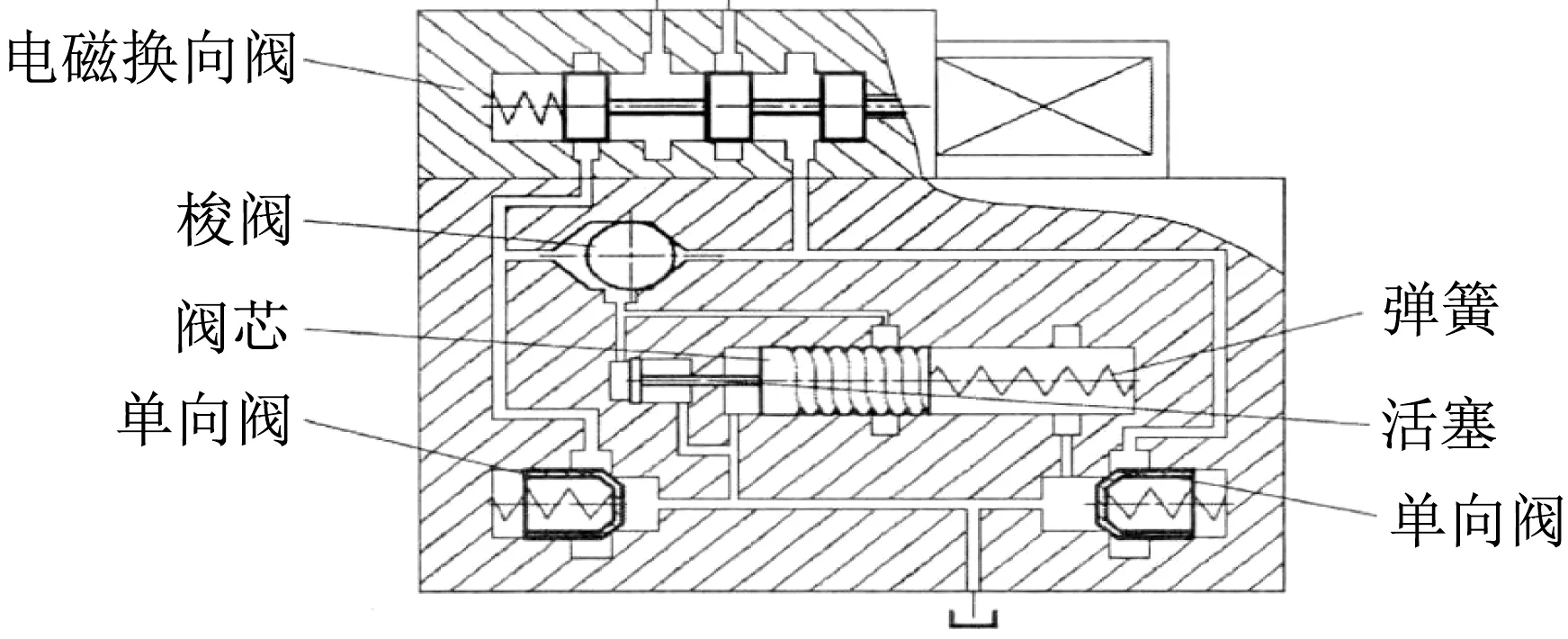
图1 负载敏感阀原理Fig.1 Schematic diagram of load sensitive valve

在负载敏感系统中，当执行元件压力改变后，负载敏感节流阀会产生差异。由液压缸制动腔压力参数实现阀芯位移的控制，形成开度不同的阀口，从而实现和负载之间的良好匹配状态，有效避免制动阶段对液压缸产生冲击作用。

1.2 负载敏感系统设计

泵控负载敏感系统原理如图2所示。

图2 泵控负载敏感系统原理Fig.2 Schematic diagram of pump-controlled load sensing system1

本次选择力士乐A10VODFR型泵［9］。在泵控负载敏感系统运行过程中，工作负载压力pL与变量泵的压力pS数据被传输到敏感阀1，并沿两端产生压力差Δp，形成弹簧力的形式。压力差范围为1～2 MPa；通过控制恒压阀2弹簧力使系统达到不同极限压力，随着负载压力增大至极限值，阀芯发生右移，油缸开启，受到压力作用后形成了最低斜盘角，此时流量快速下降到接近0。

按照以下步骤调控流量：①逐渐缩小比例调节阀的开口幅度，获得了更小过流截面A，使比例调节阀两端反馈压力差Δp发生明显变化，引起变量泵以波动状态逐渐趋近最小流量，②随着压力差Δp达到设定值时，泵完成摆动过程；③上述压力差降低后，泵以波动状态转变为最大流量，在Δp到达最初设定值时，波动过程停止。

2 模型

2.1 数学模型

构建以下阀芯运动的微分方程［11］为

式中：Ks为弹簧刚度；Av为阀芯压力感应面积；Mv为4/3倍弹簧质量；F0为预设弹簧力；xv为阀芯位移，以右方向为正。

通过变换处理计算得到负载敏感阀芯传递函数为

式中：E（s）为压力差信号；ωnv为阀体固有频率。

图3为泵传递函数的方框结构［12］。

图3 控制系统传递函数Fig.3 Transfer function diagram of control system

构建得到以下所示的泵开环传递函数W（s）：

式中：δnv为无因次阻尼系数；Kg为阀体刚度；A1为阀口截面积；cl为泄漏系数。

计算开环增益系数K：

当开环增益系数K变化后，系统运行控制性能及其响应速率也会发生改变。由此可见，负载敏感阀动态响应性能受到A1、cl参数的影响。

2.2 仿真模型

图4为泵控负载敏感系统的仿真模型。结合泵的工作原理，本文通过HCD库为泵建立了AMESim模型［13-14］。

图4 仿真模型Fig.4 Simulation model

3 结构参数对流量特性的影响

3.1 阀芯直径

不同阀芯直径下形成的泵输出流量如图5所示。由图5可知，随着阀芯直径的增大，流量可以在更短时间内阶跃上升至稳定状态，获得更快的响应速度，同时超调量发生了持续增加。d=10 mm时，泵流量输出阶跃响应性能变差，未出现超调的情况。

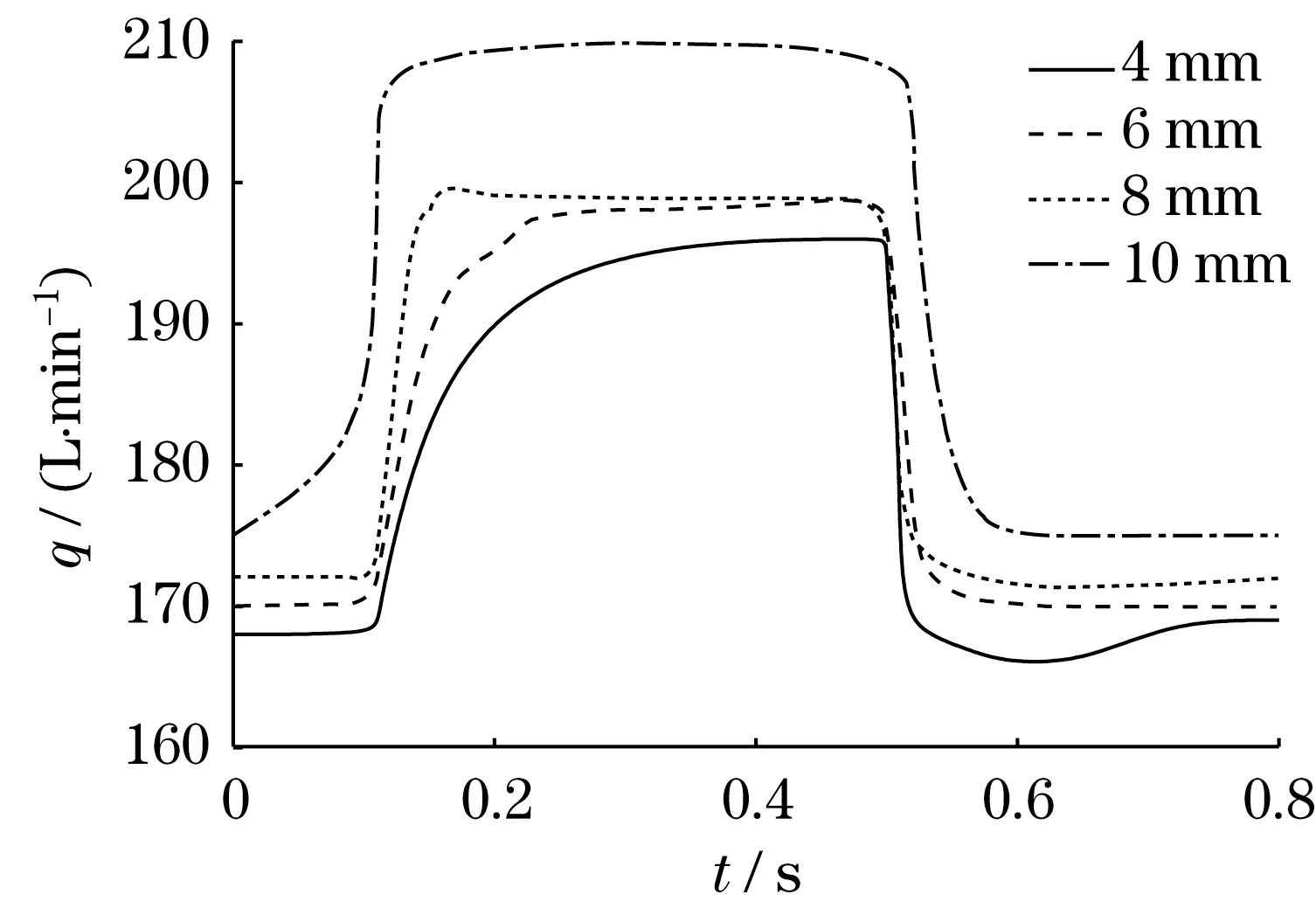
图5 各阀芯直径下形成的泵输出流量Fig.5 Pump output flow formed at each spool diameter

3.2 弹簧刚度

在各个弹簧刚度下测试得到的泵输出流量如图6所示。随着弹簧刚度的提高，可以在更短的时间内达到稳定的流量阶跃状态，同时超调量降低；在阀芯弹簧达到更大刚度时，系统将进入稳定的流量阶段，通常设定KS介于15～20 N/mm范围内。

图6 各个弹簧刚度下泵输出流量Fig.6 Pump output flow under each spring stiffness

3.3 阻尼孔尺寸

系统响应性能受到阻尼孔尺寸的直接影响。设定不同的旁路阻尼孔尺寸下的泵输出流量如图7所示。由图7可知：当旁路阻尼孔较小时，产生了更长的流量阶跃响应时间，没有出现超调的情况；随着阻尼孔直径的增大，流量阶跃可以在更短时间内达到稳定状态，同时出现了超调的情况；但需注意，过大的旁路阻尼孔会引起一定的流量波动。

图7 不同的旁路阻尼孔尺寸下泵输出流量Fig.7 Pump output flow at different bypass damping hole sizes

4 结论

随着阀芯直径的增大，响应速度加快，超调量持续增加。当d=10 mm时，未出现超调情况；随着弹簧刚度提高，系统产生了更明显振荡，通常设定介于15～20 N/mm范围内；当阻尼孔较小时，会产生更长的流量阶跃响应时间，未出现超调的情况；随着阻尼孔直径的增大，流量阶跃可以在更短时间内达到稳定状态。