多旋翼无人机磁阻尼式着陆支撑减震机构设计

莫坚，钟新利

（1.湖南铁道职业技术学院轨道交通机车车辆学院，湖南 株洲 412001；2.湖南科技大学机电工程学院，湖南 湘潭 411201）

随着高性能计算机设备的不断小型化，无人机行业得到了快速发展，而无人机未来最有前途的应用之一就是物流配送［1-3］。目前，物流业面临2个较大的问题：劳动力短缺和交通堵塞。最近，由于持续的新型冠状病毒肺炎流行病影响，物流行业受到了较大冲击。解决这些问题的最佳方案是使用无人机进行空中配送。现阶段面向物流应用的最佳无人机类型是多旋翼无人机，其所需解决的关键问题之一就是安全高效着陆［4-6］。因此，着陆时的冲击响应控制（着陆支撑减震）至关重要。

目前，多旋翼无人机稳健着陆问题尚未得到充分研究和讨论，本文主要研究的问题是利用被动机构进行冲击响应控制。被动机构是一种通用的着陆减震解决方案，可以在实现高速着陆的同时有效减少电池能量消耗。Hara等［7］和Darmawan等［8］提出利用动量交换来设计着陆响应控制机构。但是，多旋翼无人机用于物流配送时，最大化有效载荷很重要，需尽量减少着陆机构的质量。因此，不适合采用需要较大质量的动量交换式机构。Sarven等［9］尝试使用液压式减震器来加强着黏性阻尼效应以减少反弹，但是在多旋翼无人机每条支架上安装一个液压式减震器，容易发生漏油从而污染地面。此外，黏性阻尼效应会随着温度的变化而波动［10］。因此，用液压式减震器来获得恒定的阻尼效果是无效的。

基于上述讨论，本文尝试使用受环境温度变化影响最小的磁阻尼器，设计多旋翼无人机的被动式着陆支撑减震机构，并评估了所提出机构在减震时的冲击响应性能。目前，还没有关于磁阻尼器在无人机设计中应用的研究。通过数值仿真和实验研究，验证了该机构的有效性。

1 磁阻尼式着陆支撑减震机构设计

提出的多旋翼无人机着陆减震机构工作原理如图1所示。

多旋翼无人机的每条支撑腿都装有一个弹簧和磁阻尼器串联的机构，如图1（a）所示。永磁体如图1（b）所示组合在一起，并固定在机构中心轴的顶端。中心轴在着陆后立即下降，改变了磁场并产生涡流，从而产生阻尼力。由于磁阻尼器很少由于温度改变其特性，所以适用于户外场景。

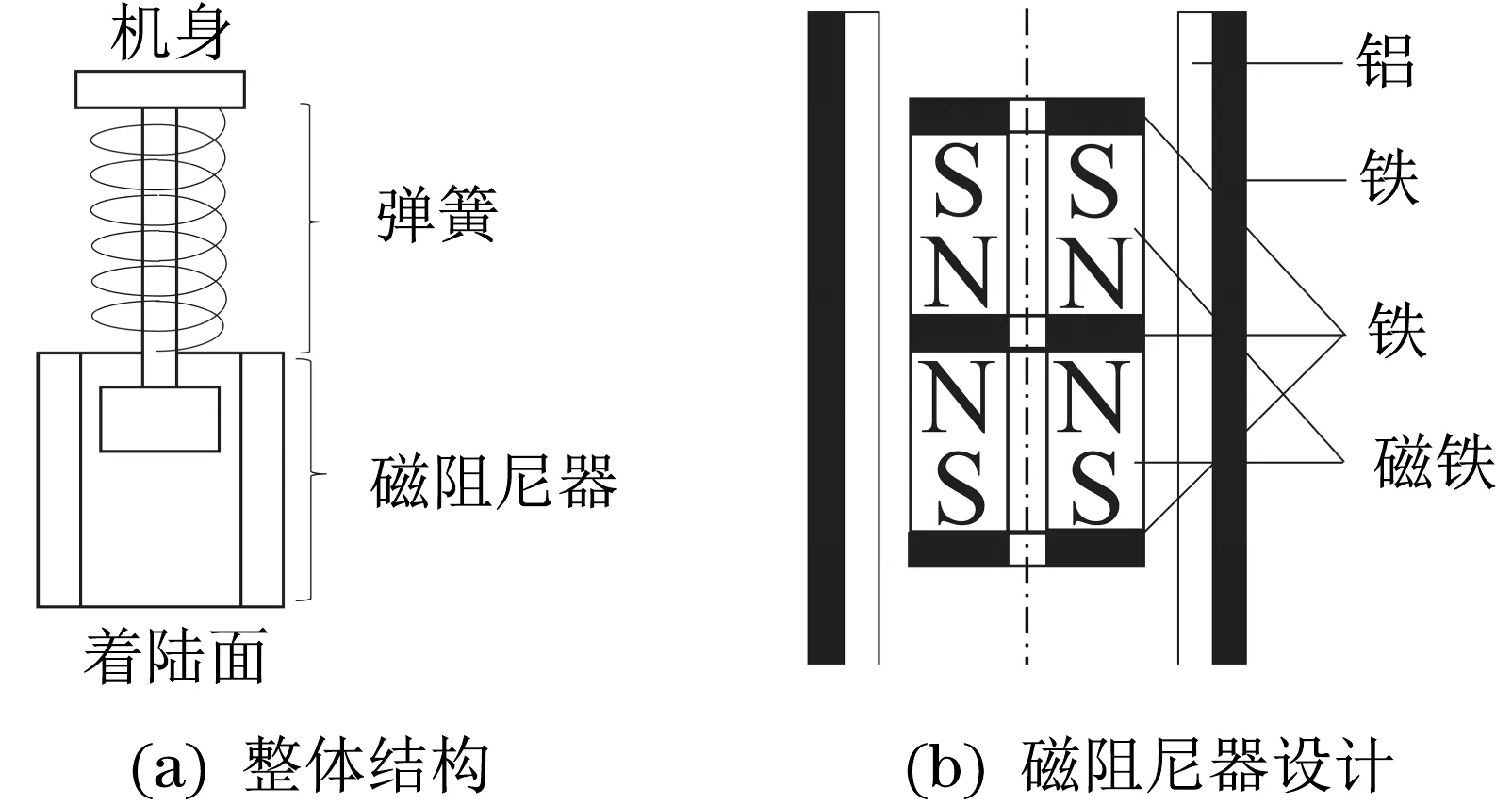
图1 着陆减震机构工作原理Fig.1 Working principle of landing damping mechanism

在图1的机构中，中心轴在着陆后立即下降，通过将部分动能转化为弹簧的弹性能来减少反弹，而剩余的大部分动能则转化为磁体的阻尼能量。大型永磁体很重，不适合多旋翼无人机。然而，即使在有限的体积和质量条件下，通过组合多个永磁体，磁通量密度也可以增加，如图1（b）所示。此外，这种组合允许高密度磁通量垂直进入导体，提高了阻尼性能［11］。将图1（b）的由铁和铝组成的外部元件定义为“外圆柱部分”，将中央永磁体元件定义为“磁铁部分”。为了最大化有效载荷质量，磁阻尼器的设计必须在尽量减轻重量的同时最大限度地提高阻尼性能。

2 数值模拟验证

2.1 机构建模

对设计的着陆减震机构进行建模，并通过数值模拟验证其有效性，机构模型如图2所示。

图2 机构模型Fig.2 Mechanism model

图2（a）显示了表示模型特定部分的符号，图2（b）显示了模型的参数设置。模型参数的说明见表1。

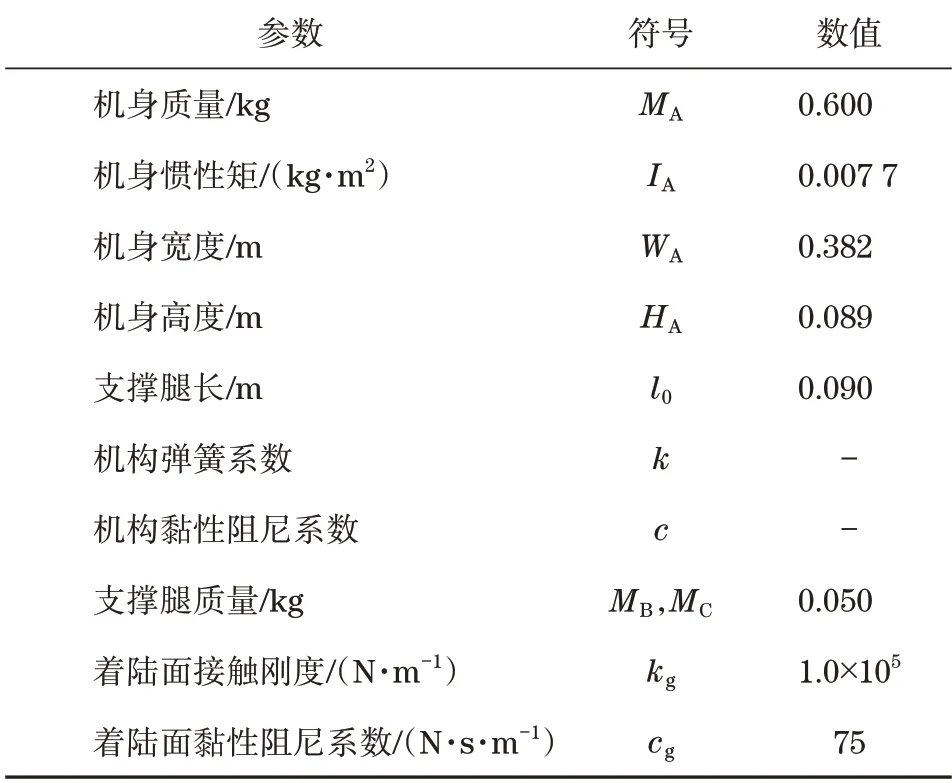
表1 模型参数的说明Tab.1 Description of model parameters

图2中的模型由3部分组成：无人机的机身、左支撑腿和右支撑腿，分别命名为A、B和C（A1到A4为模型上的不同位置，不是机身）。这里忽略了支撑腿的逆时针惯性矩。机身和每条支撑腿之间使用弹簧和阻尼器进行连接。由于在着陆过程中弹簧的恢复力和磁阻尼器的阻尼力同时作用，因此该机构模型中弹簧和磁阻尼器是并联的，且假设弹簧释放弹性能量的周期与磁阻尼器产生阻尼力的周期完全重叠。

利用多体动力学［12］，对图2（a）所示模型推导出如下运动方程：

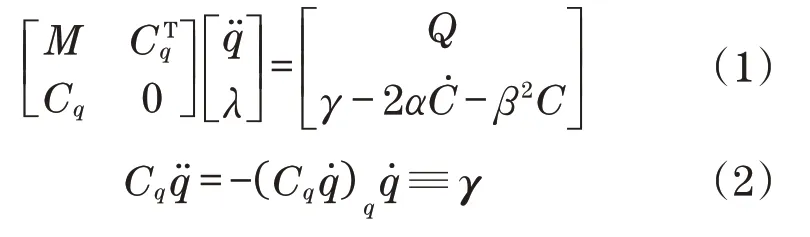
式中：C为约束矩阵；q为广义坐标；M为广义质量矩阵；Q为广义力矩阵；γ为设计参数；α、β为稳定C的反馈增益，在此模拟中设置为50。条件C用于约束支撑腿和机身之间的关节运动：

式中：ϕ为角度；r为位置矢量。

2.2 设计参数优化方法

为了最大化无人机的有效载荷能力，必须同时实现磁阻尼器的减重和阻尼性能的最大化。因此，需要设计最佳的弹簧系数k和黏性阻尼系数c。根据式（1）～式（3），利用Matlab/Simulink进行数值模拟，确定k和c。为简化分析，假设着陆为突发紧急自由落体，且下落时没有大的倾斜。着陆面到支撑腿末端的初始高度设置为0.3 m，其他模拟参数见表1。在上述条件下，计算不同设计参数k和c情况时的冲击响应，最大行程和最大反弹结果分别如图3、图4所示。

图3 最大行程变化Fig.3 Maximum stroke change

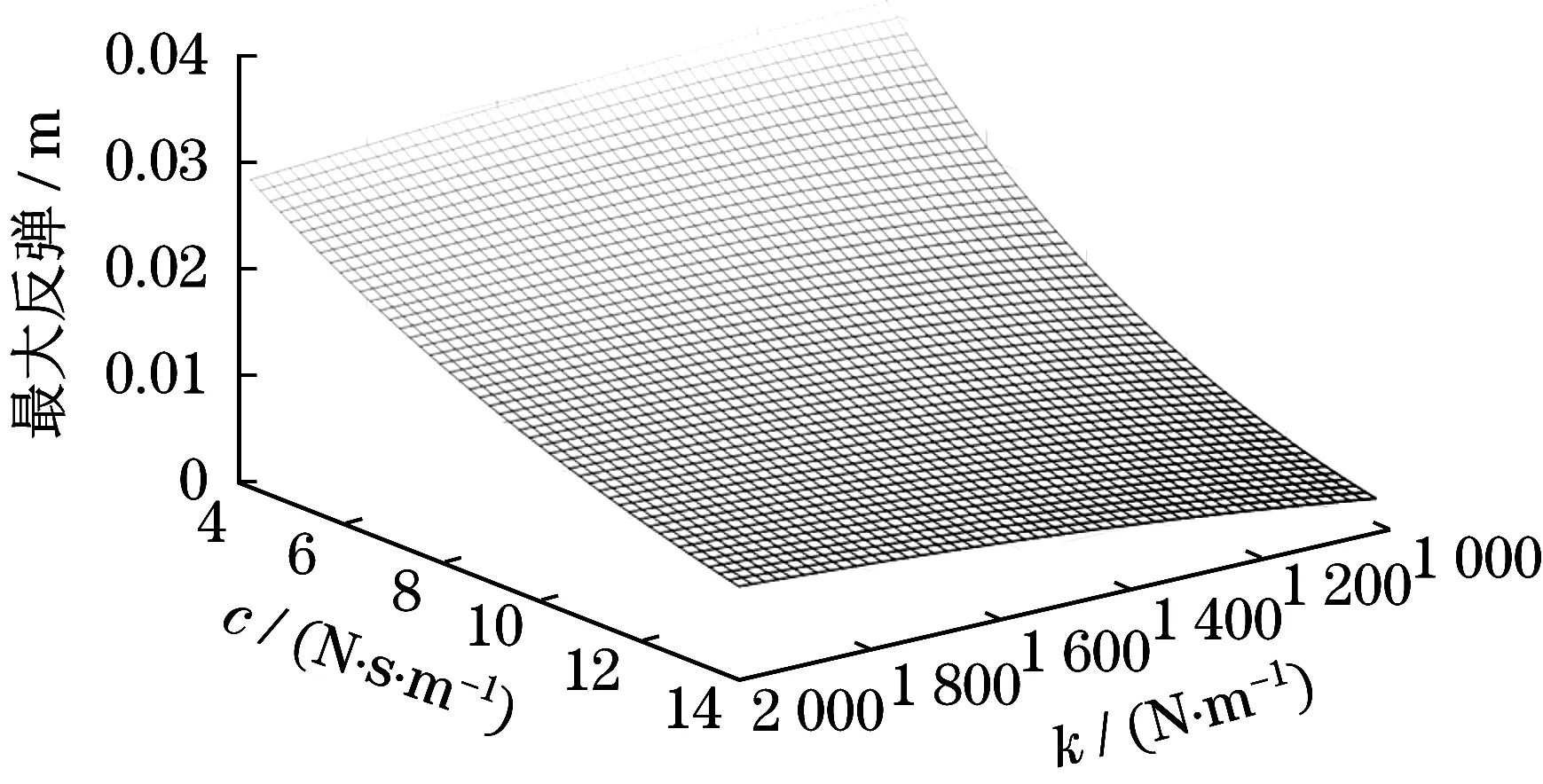
图4 最大反弹变化Fig.4 Maximum bounce change

最大行程是指支撑腿的最大收缩量，而最大回弹是指落地后支撑腿的最高位置。参数k和c的详细设计步骤如下：

步骤1无人机的质量要尽可能做到最小化。因此，在满足磁阻尼器极限质量的前提下，可以根据材料的密度和强度，初步确定“外圆柱部分”和“磁铁部分”的尺寸。最大行程的限制取决于为“外圆柱部分”的长度。如果不满足这个极限，磁铁将与外圆柱体的端面相撞，落地的冲击可能会损坏磁铁。

步骤2确定机构黏性阻尼系数c。对于图1（a）所示的结构，虽然随着磁体的下降，磁通发生变化，黏性阻尼系数c也发生变化，但是磁体下降距离很短，磁通变化较小［13］，因此可以假设c为恒定的，从而采用电磁场分析软件JMAG来确定c的数值［14］。

步骤3利用已确定的黏性阻尼系数c来确定机构弹簧系数k。从图4中可知，减小弹簧系数k可以减小最大反弹。因此，在黏性阻尼系数c确定的条件下，k越小越好，同时要求不能超过图3中的最大行程。

对上述设计参数优化方法进行了举例说明。在图2（a）所示的模型中，“外圆柱部分”的质量由B或C的质量构成，“磁铁部分”的质量由A的质量构成。“磁铁部分”采用钕铁硼磁铁（N52）和冷轧钢板（SPCC）。“外圆柱部分”采用铝（1070A）和一般结构用钢材（SS400）。“外圆柱部分”和“磁铁部分”均为圆柱体。在图3和图4中，“磁铁部分”自由落体的典型速度［15］被设置为4.0 m/s。

2.3 数值模拟

在数值模拟中，将黏性阻尼系数c设置为8.8 N·s/m，将弹簧系数k设置为1 200 N/m。为了验证磁阻尼式机构的有效性，比较了其与刚性杆模型在着陆时的时程反应［16］。刚性杆模型使用刚性杆代替了支撑腿的弹簧和阻尼器。在该模型中，调整机身质量以使总质量与原始模型的总质量匹配，且表示约束条件的矩阵C为

式中：rAB为B相对于A的相对位置矢量；rAC为C相对于A的相对位置矢量。

在磁阻尼式机构或者刚性杆的作用下（自由落体），机身A重心的时程反应对比如图5所示。

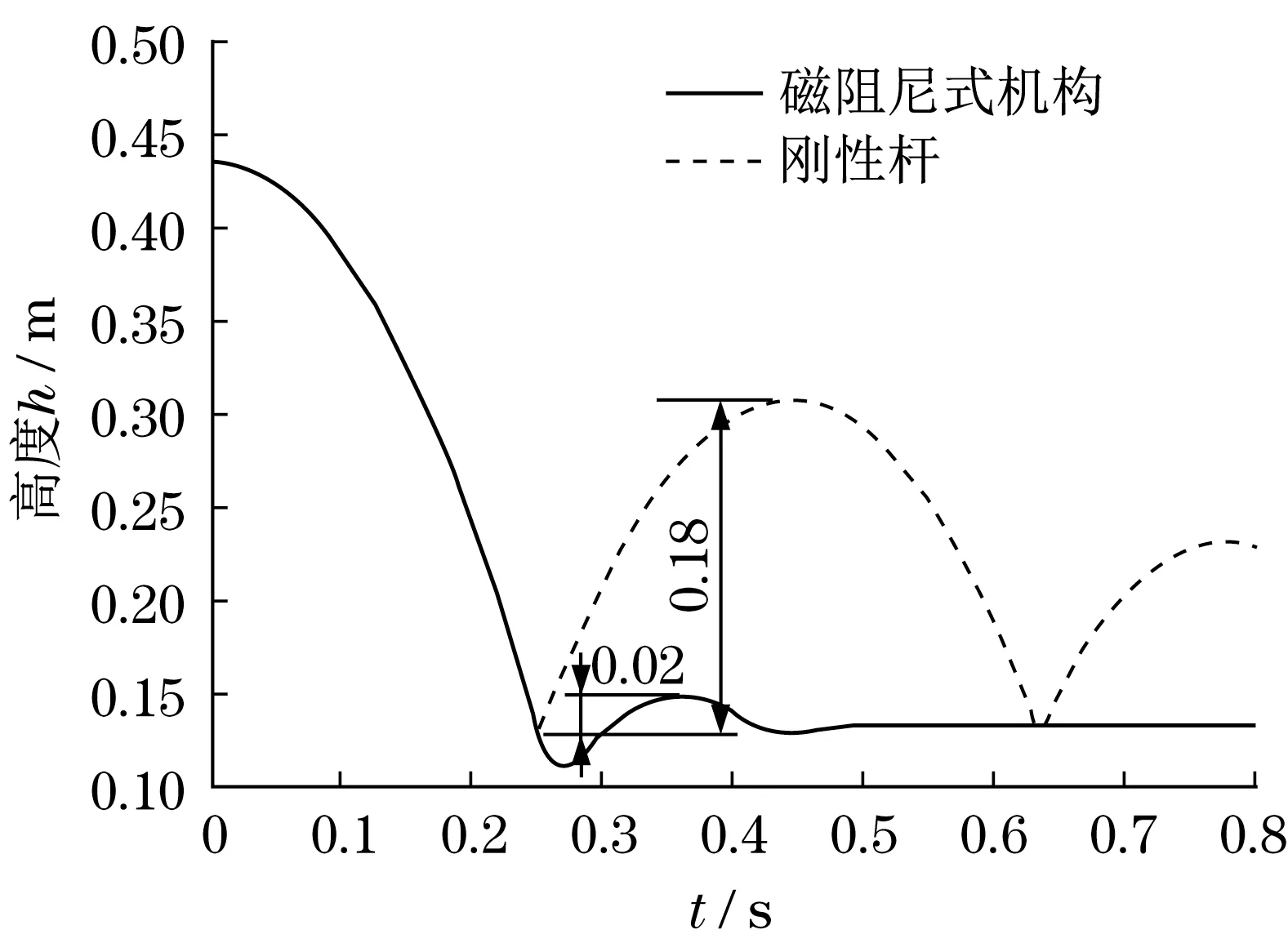
图5 模拟中的时程反应对比Fig.5 Comparison of time-history response in simulation

由图5可知，刚性杆模型的最大反弹约为高度0.18 m。磁阻尼式机构实现的最大反弹仅约0.02 m，减少了88.9%。因此，数值模拟结果验证了所提机构的有效性。

3 实验结果与分析

3.1 实验装置

在自由落体数值模拟之后，通过实际测试对磁阻尼式机构有效性进行了进一步验证。该磁阻尼式减震机构由弹簧和磁阻尼器组成，其中螺旋弹簧的弹簧系数为1 200 N/m，磁阻尼器的材料和尺寸与前一节中JMAG模拟的数值相同。最终制备的磁阻尼式减震机构的质量仅为94.5 g，如图6所示。

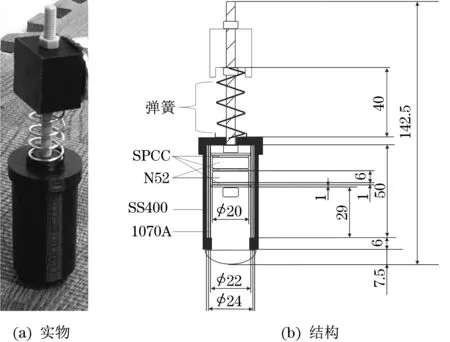
图6 制备的磁阻尼式减震机构Fig.6 Magnetic damping damping mechanism prepared

冲程的实际值为29 mm，满足大于设计的最大行程。在实验中，高度设置为0.3 m（着陆面到支撑腿末端），与数值模拟的设计参数相同。实验过程中使用了2种类型的橡胶板（SGNB和SUTLL）作为着陆面，以考虑对地面参数变化的敏感性。2种橡胶板的参数见表2。

表2 2种橡胶板的参数Tab.2 Parameters of two rubber plates

3.2 结果分析

在相同实验条件下，实验与模拟的结果对比如图7所示。

由图7可知，模拟结果与实验结果完全一致。此外，为了进一步验证实验的可重复性，对每种着陆面进行了10次实验。重复实验的结果如图8所示。

图7 实验与模拟的结果对比Fig.7 Comparison of experimental and simulation results

由图8可知，不同着陆面时10次实验绘制出来的时程反应结果几乎完全重叠。因此，提出的减震机构有效性得到了验证，且不受地面参数变化的影响。

图8 10次重复实验的结果Fig.8 Results of 10 repeated experiments

4 结语

本文提出了一种基于磁阻尼器的着陆支撑减震机构。针对黏滞阻尼系数和弹簧常数2个主要设计参数，提出了在JMAG数值模拟中，以最大行程和最大反弹为阈值的参数设计方法，从而在实现机构质量最小化的同时尽量提高着陆时的减震性能。根据所确定的参数，通过数值模拟和实验对机构的有效性进行了验证。磁阻尼式机构的质量仅为94.5 g，最大反弹高度比刚性杆降低了88.9%，仅约0.02 m。后续将对以倾斜角度着陆的问题展开研究，并尝试进一步探讨基于冲击力大小的变黏阻尼机构的可行性。