一道“希望杯”赛题的多角度探究

广东梅县东山中学 (514017) 钟国城

此题虽条件简洁,但内涵丰富,解法灵活多样,能开拓解题视野,提升解题能力与核心素养,是一道值得深入探究的好题.下面从不同角度给出本题的多种解法,以供大家欣赏.

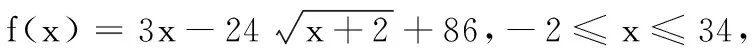
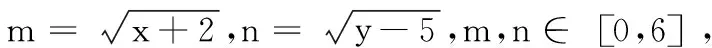
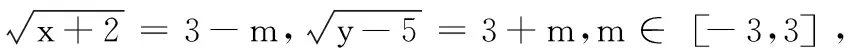
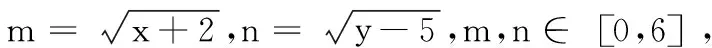
综上,得x+2y的最小值是32,最大值是80.

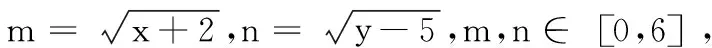
解法6:(利用一元二次方程根的分布)

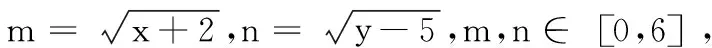
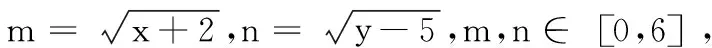
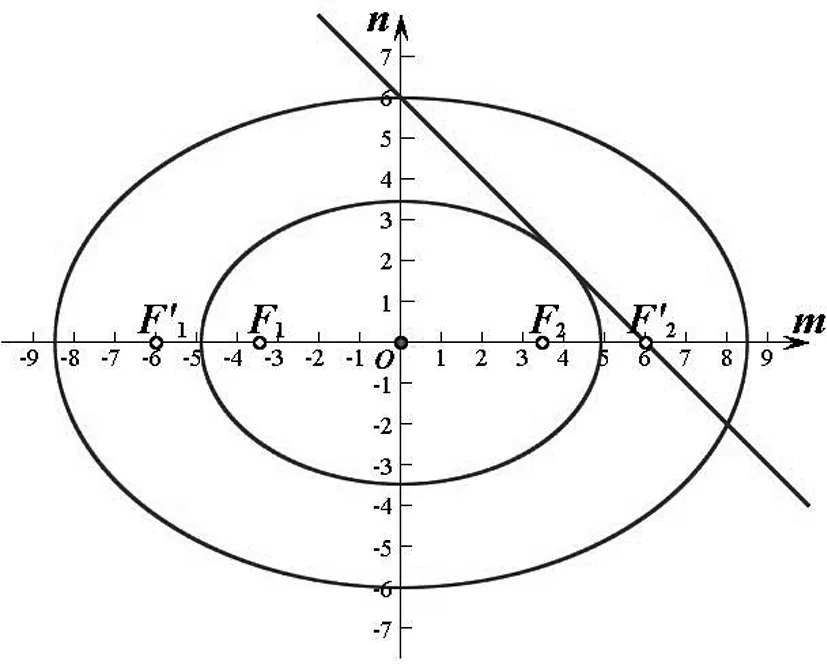
图1

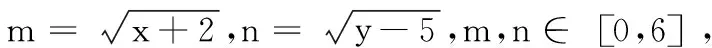
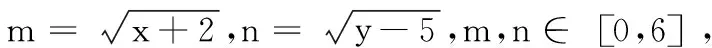
解后反思：数学解题的目的是什么?是求出问题的答案吗?是,但不全是.解题的目的是巩固数学基础知识与基本技能,领悟数学思想,提升数学思维.一道典型的数学问题蕴含着丰富的数学知识和方法,通过对这样的数学问题不断追问其多种解法,把所学知识都联系起来,让学生领会数学知识八方联系浑然一体,充分领略数学的魅力,从而发自心底热爱数学,享受数学解题的过程,因此,对一道经典数学问题的多角度探究式非常有必要的.

一题多解是提高解题能力的有效途径,不但拓宽了学生思维的灵活性与深刻性,对学生数学思维能力的培养能起到了潜移默化的作用,而且提高了学生解题的品位与效率,激发了学生学习数学的兴趣.通过以上10种解法的探析,不仅可以巩固学生所学知识, 又有效锻炼了学生思维的深刻性、广阔性、灵活性和创新性,提升思维能力,最终达到提升学生数学核心素养的目的.