一道立体几何调研题的解法赏析

湖南师范大学附属中学1907班 (410006) 赵斯扬 湖南省长沙市雷锋学校 (410217) 童继稀 邓捷敏

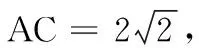
这是武汉市2022届高中毕业生四月调研考试卷第16题，它以三棱锥为背景，点到线与点到面的距离求解为设问，全面考查点、线、面的位置关系等基础知识，以及数学转化、推理论证和运算求解等关键能力．其难点体现在图象处理与转化求解，即如何将这样一道空间问题转化成学生们更加容易理解的问题．本文给出多种解法，与读者分享交流．

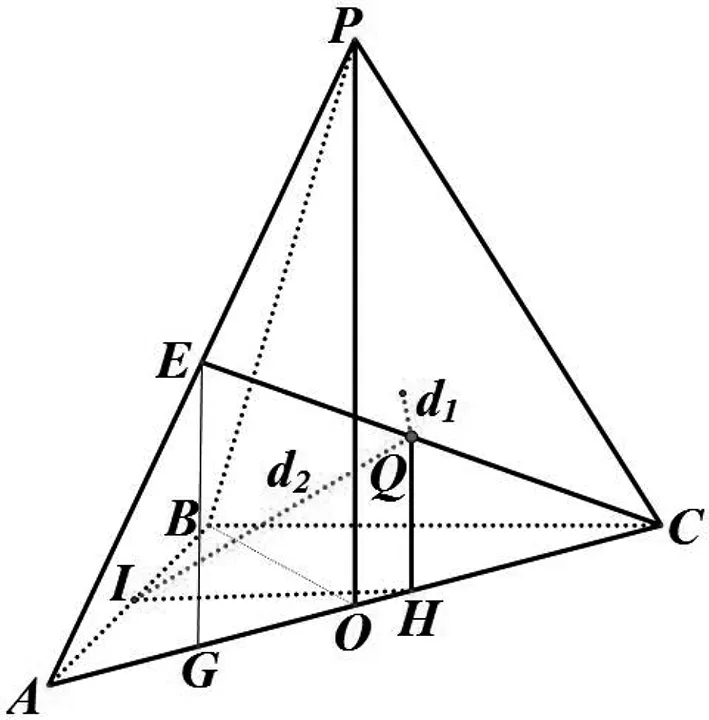
图1

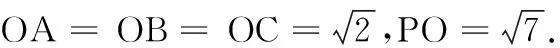
以下对第二空从多个角度求解.

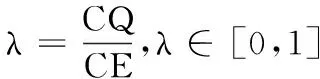
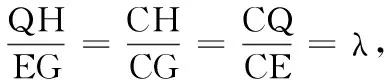
综合法解立体几何问题离不开作辅助线，这恰好是学生难以突破的困境．从该三棱锥形状来看，不难发现线段AC，OB，OP两两垂直，我们可以建立空间直角坐标系，通过空间向量求点到直线与点到平面的距离公式表示出d1+d2，再求得最值．

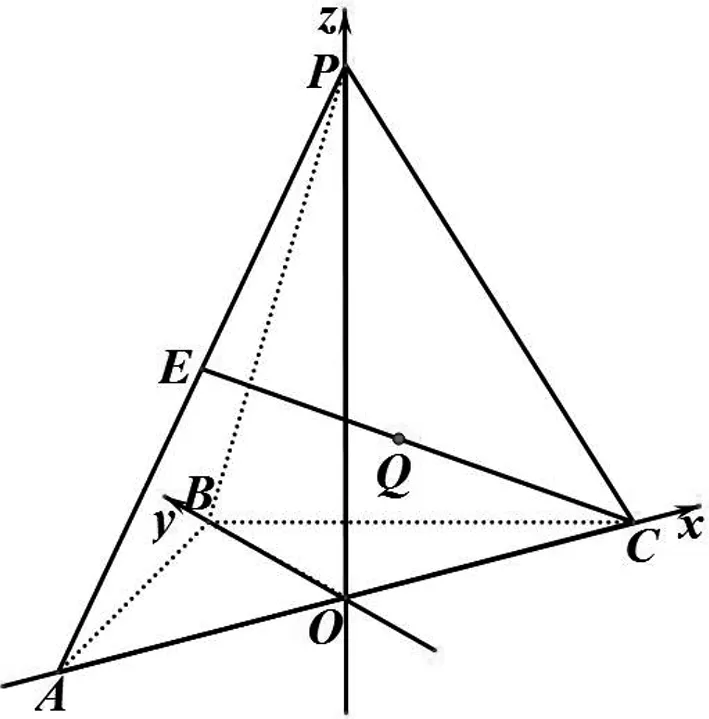
图2

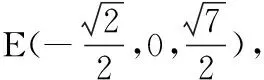
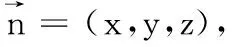
坐标向量法利用数及其运算来解决问题，思路简洁，但计算有点繁杂．从该三棱锥形状的另一角度看，我们可以将它补形成一个正四棱锥来求解．

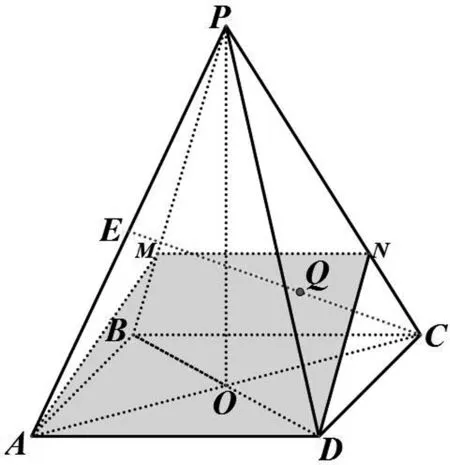
图3

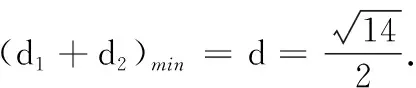
本题也可利用点Q到平面PBC的距离等于Q到平面PCD的距离，同思路求解；还可将三棱锥补形成长方体求解，过程留给读者．

解法3的优势在于利用了图形的对称性，将题中所求的距离转化为更加直观的线面距离，计算量少，但又很难想到这样补形处理．综合法、向量坐标法与转化法在解决立体几何相关问题中，各有利弊，往往需要我们根据问题情境来选择最适合的方法求解．2020年与2021年的新高考Ⅰ卷都把立体几何小题放在选择题或填空题的压轴位置，加之新教材重新引入了距离公式，从而我们教学时更需重视这类问题．