构造向量数量积巧解几类数学题

广东省惠州市第一中学 (516007) 李海媚 方志平

我们知道向量集“数”、“形”于一体,尤其是在向量的数量积中，向量模长乘积反映了“数”的特征，向量夹角的余弦反映了“形”的特征.向量数量积的特征决定了它是数学知识的一个交汇点，运用它容易看到知识之间的内在联系和相互作用，为我们解决数学问题提供了更为广阔的思维空间．有些看似与向量无关的题目，通过构造向量数量积作为“载体”, 可以使很多棘手，繁杂的问题得以合理、顺利地解决.本文例析构造向量数量积，巧妙解决几类数学问题，希望对同学们的数学学习有所启发.

1.巧解函数的值域问题

图1

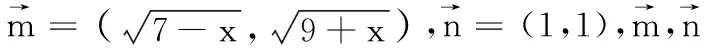
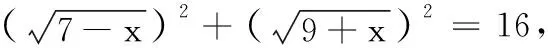
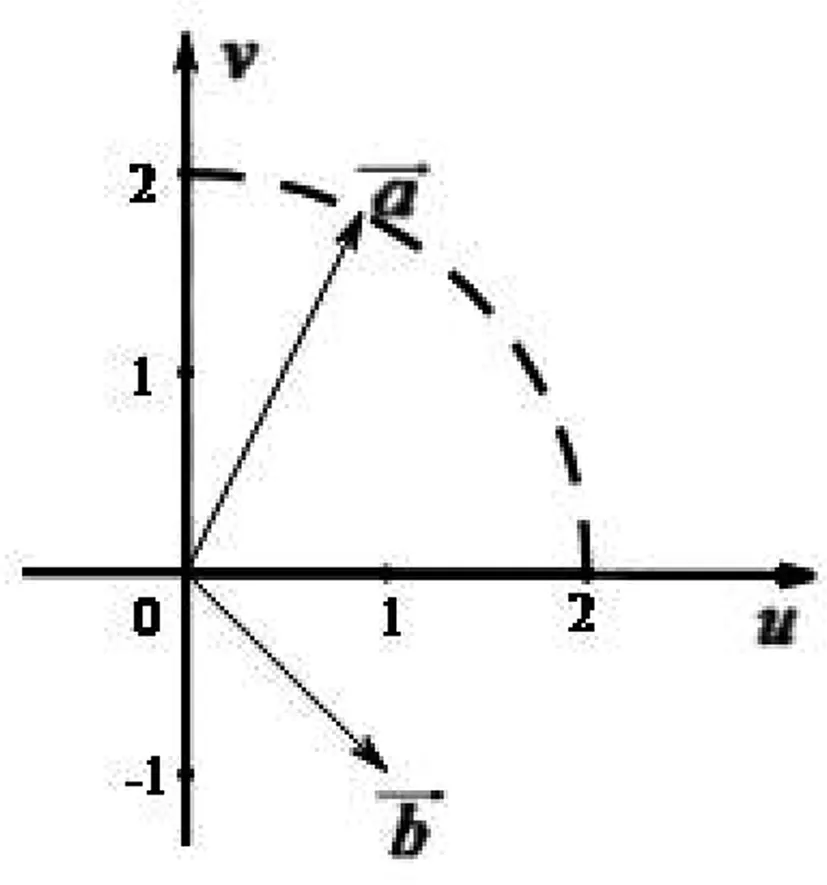
图2

∴y∈[-1,3].故原函数的值域是[-1,3].

2.巧解与三角有关的问题

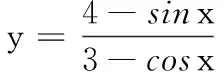
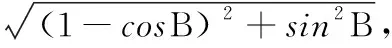
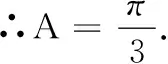
3.巧解代数式的最值问题

例5 设x,y为实数，若4x2+y2+xy=1, 则2x+y的最大值是.

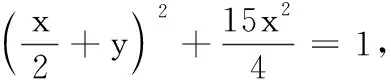
4. 巧证相关不等式问题

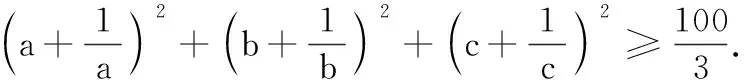
我们在构造向量的过程中，首先要观察题设条件或结论的结构特征，必要时要对条件或结论进行变形，转变成我们所熟悉的向量模型，再利用向量所具有的性质和定理进行求解．本文中将几类相关问题转化为向量的数量积问题，不仅可避繁就简，而且方法新颖，独辟蹊径.构造向量数量积解题可提高学生思维的发散性，开拓他们的思维空间，也是培养学生创新能力的好素材.