例谈比较大小的处理方法*
福建省泉州市第七中学 (362000) 林 婷 杜成北
比较大小是历年高考的热点,常作为选择压轴题出现,对于大部分学生来说是一个难点,需要去重点突破.在比大小求解过程中突出考查学生的基础知识、基本技能以及基本数学思想,提升了学生的思维品质,发展了学生的数学核心素养.本文以2022年八省T8联考第8题为引例,谈谈比较大小的一般处理方法.
1 题目呈现
(T8联考2022届高三第一次联考第8题)设a,b都为正数,e为自然对数的底数,若aea+1+b A.ab>eB.b>ea+1C.ab 本题的命题思路源于2020年高考全国Ⅰ卷理科第12题:若2a+log2a=4b+2log4b,则( ). A.a>2bB.a<2bC.a>b2D.a 高考数学选择题中常常出现与指数、对数相关比较大小问题,此类问题看似简单,实则涉及较多的知识点和处理方法,及一般到特殊、转化与化归、数形结合等数学思想,是凸显学生思维品质,提升数学核心素养的常见载体.为了让考生更好突破该知识点,笔者将比较大小的常见处理方法归纳整理. (1)巧作差(作商),比大小 例1 (2020年课标Ⅲ卷理科第12题)已知55<84,134<85.设a=log53,b=log85,c=log138,则( ). A.a C.b (2)巧放缩,比大小 例1中a,b的大小关系也可以利用作差,通过基本不等式和适当放缩来比较: (3)巧搭桥,比大小 “搭桥”法是通过寻找中间数,一般用“0”和“1”或其他特殊值进行“搭桥”,比较两个数值的大小. A.x C.z (4)巧构造,比大小 例3 (2020年八省联考第8题)已知a<5且ae5=5ea,b<4且be4=4eb,c<3且ce3=3ec,则( ). A.c C.a (5)巧转化,比大小 A.a C.a 总之,本文中的求解比较大小问题,要注意关注式子之间的区别,建立恰当联系.应该从多个维度发现问题,分析问题,解决问题.2 题目探源
3 思路探析
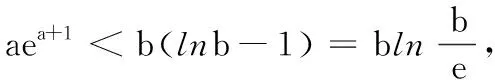
4 探究归纳
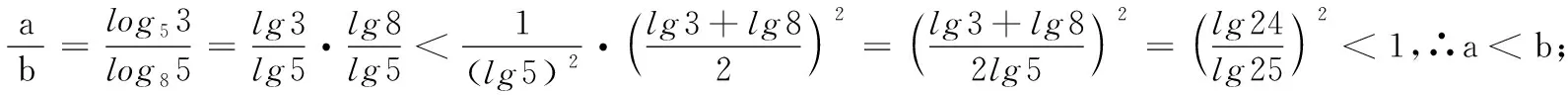
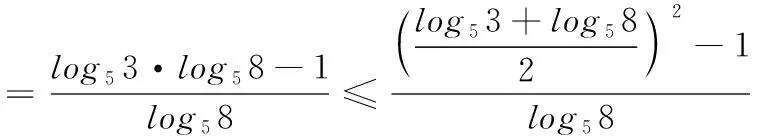

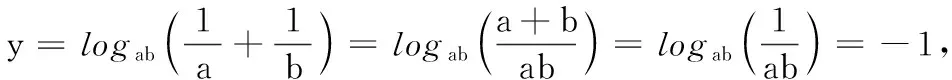
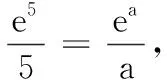
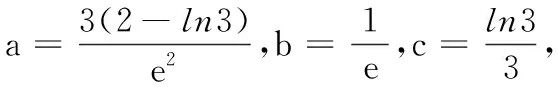
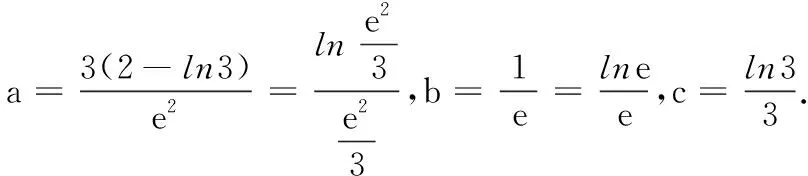
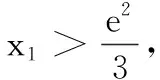
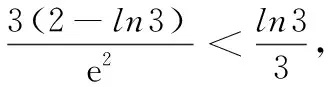
5 反思总结

