对一道2015年浙江预赛附加题的再探究

浙江省台州市玉环中学 (317600) 邬仁勇浙江省嘉兴市第一中学 (314050) 沈新权

文[1]对2015年全国高中数学联赛浙江预赛附加题1的解法作了探讨，得到了一些新的结论，并对试题作了推广，读后很受启发．我们在文[1]的基础上对这个问题及其解法作了进一步的探究，得到了二阶线性递推关系与另外两个递推关系的等价结论，结合模数列周期性的结论，对文[1]留下的三个困惑作了研究和思考，提出了我们的看法．为了方便阅读，我们将原题呈现如下：

已知数列{an}满足a1=1,an+1=3an+

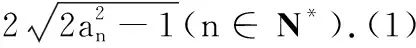
1. 三个等价的递推关系

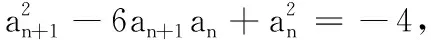
利用上面的分析方法，我们可以得到下面的更一般性的结论，结论的证明请读者自行完成．

定理1 如果数列{an}(其中an+2≠tan,n=1,2,… )满足下列三个递推关系中的一个，那么它也满足其余两个递推关系(其中s,t≠0为常数)：

(1)an+2+san+1+tan=0 ②；

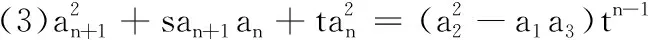
也就是说，上面的②③④三式是等价的．

2 困惑(3)、(2)的思考

上面的讨论方法以及定理1的这几个结论，对我们思考困惑(3)、(2)有很大的启发．

3 困惑(1)的思考

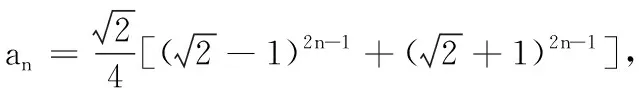
下面我们利用同余的性质来证明数列{an}的项被31除所得到的余数的周期为15.

因为an+2=6an+1-an且a1=1,a2=5，所以a3=6a2-a1=6×5-1≡29(mod31)，a4=6a3-a2≡6×29-5≡6×(-2)-5≡14(mod31)，为了节省篇幅，接下来我们只列出同余式：a5≡24(mod31)，a6≡6(mod31)，a7≡12(mod31)，a8≡4(mod31)，a9≡12(mod31)，a10≡6(mod31)，a11≡24(mod31)，a12≡14(mod31)，a13≡29(mod31)，a14≡5(mod31)，a15≡1(mod31)，a16≡1(mod31)，a17≡5(mod31)，于是，由递推式an+2=6an+1-an并结合数学归纳法可以证明，模数列{an(mod31)}是周期为15的周期数列，即如果我们记模数列{an(mod31)}为{bn}，则对于一切的n∈N*，数列{bn}满足bn+15=bn．

为了让读者进一步了解递推数列的模数列的周期性，我们再给出定理2，有兴趣的读者可以参阅文[2]证明．

定理2 已知数列{an}满足an+2=c1an+1+c2an(n∈N*)，其中a1,a2，c1,c2都是整数.如果(ci,m)=1(i=1,2)，则模数列{an(modm)}是周期数列.

在定理2的基础上，我们回过头再来思考2015年全国高中数学联赛浙江预赛附加题1第(2)小题的解法，这种思考会给我们今后解决这类问题带来一定的启发．附加题1的第(2)小题是要我们判断是否存在m∈N*，使得2015|am．由于数列{an}满足递推关系an+2=6an+1-an，由定理2我们知道用与6互素的数去模数列{an}中的项，其模数列必定是周期数列．因此，要解决第(2)小题，我们需首先考虑用2015的质因数5，13以及31去模数列{an}中的项，由a1=1,a2=5及递推关系an+2=6an+1-an，容易验证a2≡0(mod5)，a4≡0(mod13)，所以，为了解决问题，我们只能选择31去模数列{an}中的项，由于{an(mod13)}是周期数列，因此，接下来的事情我们只需要通过a1=1,a2=5及递推关系an+2=6an+1-an找到{an(mod13)}一个周期里面的所有的项(余数)中没有一个为0，问题就解决了．至此，文[1]中的困惑(1)彻底解决．