一道质检题的再探究

广东省珠海市实验中学 (519090) 夏 莹

题目(2022年石家庄高三质检三第16题)△ABC的三边分别为a,b,c,若a2+b2+2c2=8，则△ABC面积的最大值为.

笔者在进行高三复习教学中遇到上题，此题对学生来说有一定的难度，在此给出如下两种易想的解法(其他解法再次不再一一赘述)，希望能起到抛砖引玉的作用.

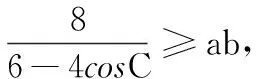
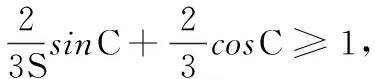
事实上，我们解决上面的问题后，可以作适当变式探究：

探究1 △ABC的三边分别为a,b,c,若a2+b2+c2=8，则△ABC面积的最大值为.

探究2 △ABC的三边分别为a,b,c,若a2+2b2+3c2=8，则△ABC面积的最大值为.

探究3 △ABC的三边分别为a,b,c,对于任意给定的正数m,n,k，若ma2+nb2+kc2=8，则△ABC面积的最大值为.

对于Weisenbock不等式证明方法有很多，我们不再一一赘述.

对于探究2、探究3，明显难度进一步加大，事实上，我们也可以得到更一般的结论.

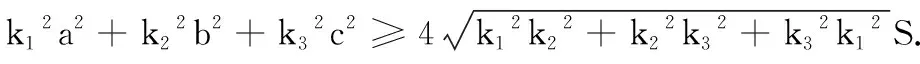
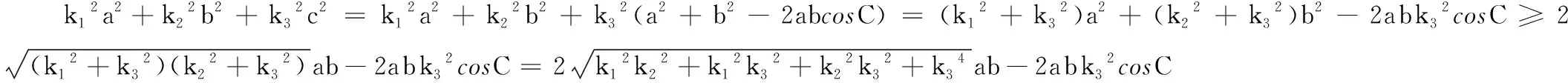
结论1显然是探究1、2、3的推广情况.事实上，对于结论1，我们仍然可以做出进一步的推广.

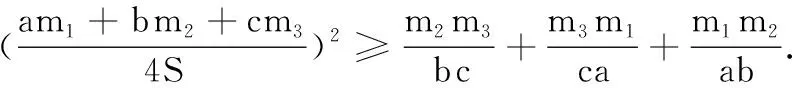
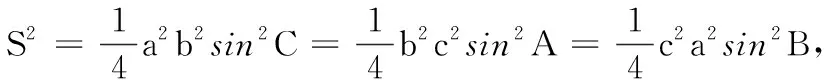
-2[bcm2m3cos2A+acm1m3cos2B+abm1m2cos2C]

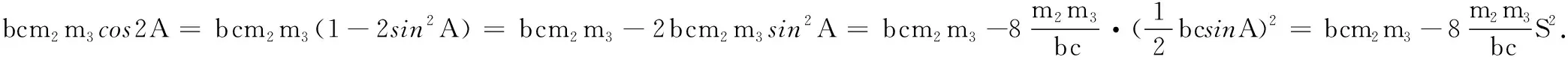
在结论2中我们取则结论2即变为结论1，所以结论1是结论2的特殊情况.