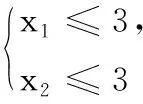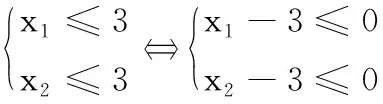例谈“充分与必要”的三类应用

福建省古田县第一中学 (352200) 兰诗全

数学解题过程一般是寻找充要条件的过程，但有时寻求原问题的充要条件是很困难的，或所寻求的充要条件很繁，不便于求解．此时，可以先找到使结论成立的一个充分条件，再一步一步逼进找到使结论成立的充要条件；也可以考虑从原问题的一个较弱的必要条件开始，挖掘出问题的隐含条件，寻找解题的突破口，进一步探究原问题的充要条件．以上这三类都是很重要且非常实用的解题方法，现结合例子加以说明．

1 先充分再充要

先根据已知找到一个使结论成立的一个充分条件，再顺水推舟地一个一个把所有的解都找回来，或说明没有其它解，最后得到问题的准确解．

例1 已知a∈R时，f(x)=x(ex-2a)-ax2，当x∈R时，f(2x)≥2f(x)，求a的取值范围．

解：f(2x)≥2f(x)⟺xe2x-xex≥ax2①．

当x=0时，①式恒成立；

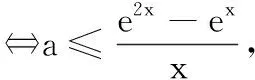
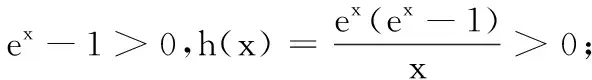
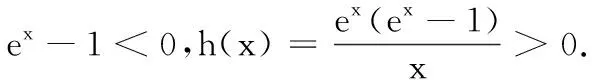
故当a≤0时，①式恒成立．(即找到了使当x∈R时，f(2x)≥2f(x)恒成立的一个充分条件．)

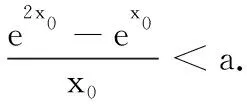
以上“先充分再充要”在实际解题中是很有用的，许多分类讨论方法也是归于此类，充分与必要，二者都需要，要明白根本原理，才能思路清晰，正确解题．

2 先必要再充要

解题成功的关键是能及时准确地找到解题的突破口，如何寻求解题的突破口？方法之一是可以巧用原问题的必要条件，再在这个必要条件的基础上寻找突破口，充分体现必要条件的解题功能．

例2 设0(ax)2的解集中的整数个数恰有三个，求实数a的取值范围．

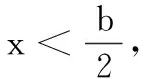
(即先找到使结论成立的一个必要条件，在这基础上再研究．)

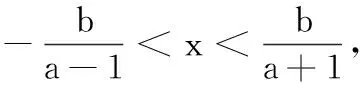
本题关键利用二次函数图象求出恰有三个整数解的一个必要条件a>1，在这个必要条件下求出原不等式的解集是一个开区间，再在这个必要条件下，求出区间右端点只能在某一小区间内活动，从而由已知可确定这个区间的三个整数，进而得出这个区间左端点的活动区范围，列出不等式，最后求出1

3 直接充要

对充要条件是否准确应用直接关系到解题的成败，许多时候解题都是因为充要关系没用好而致错，对充要条件应用要十分注意，要从错解中明白错因，要从正解中认识解题的原理，要形成专题不断巩固，要构成数学思想方法，发现解题的规律性与本质性．

例3 已知方程x2-(m+1)x+4=0在x∈(-∞,3]上有两个不同的实数解x1,x2，求实数m的取值范围.

需要说明的是，证明不等式(或等式)，只要求每一步的结论须是前提的必要条件，但解不等式(或方程)要求的是同解过程，即必须是：“充分且必要”条件即等价转化，不能只是必要条件或充分条件，这是关键，这是本质．对充分与必要条件的应用要深刻准确，根据问题的不同特点，区别对待，给出不同的解题方法，领悟解题规律，才能思路清晰，准确解答，故特作以上三类解法的归纳与总结．