基于上采样金字塔结构的卷积神经网络的非侵入负荷辨识算法

杜宇，严萌，武昕

（华北电力大学 电气与电子工程学院，北京 102206）

0 引言

随着我国能源改革的推进［1］，需求侧管理的重要性日益凸显。作为需求侧管理的基础，用户用电数据质量决定着需求侧管理的精细程度。通过对用户负荷进行监测，获取用户实时用电数据，可以为相关电力政策的制定提供数据支撑，为用户改善用电行为提供建议［2］，引导用户合理规划用电时间，进而实现高效的需求侧管理。

负荷监测技术分为侵入式和非侵入式两大类。侵入式负荷监测主要是通过对用户的每个用电器安装信息采集设备，获取电器用电信息。虽然该技术得到的数据准确可靠，但是耗资巨大，不利于推广［3］。相较于侵入式负荷监测，非侵入式负荷监测（Non-Intrusive Load Monitoring，NILM）对于用户影响小，成本低更具有实用性。负荷辨识是负荷监测中重要的一环，传统负荷辨识算法都需要从采集到的电流电压信号中提取先验数据。如文献［4］中基于有功和无功功率进行负荷辨识，文献［5］中根据动态时间弯曲算法计算实测数据和先验数据的距离来完成负荷辨识。随着智能算法的发展，大量研究以人工提取特征作为训练数据，通过构建分类模型进行负荷辨识。文献［6］中提出一种基于滑动窗的双边累积和变点检测算法，但没有具体提出检测暂态过程后的负荷识别方法。文献［7］中提出基于全局与滑动窗口相结合的注意力机制的负荷分解模型。文献［8］中提出一种利用粒子群优化（Particle Swarm Optimization，PSO）优化神经网络参数的方法，提高神经网络的NILM 精度。文献［9］中将电流信号进行小波变换从中提取特征作为神经网络的训练数据，并用构建的神经网络对负荷进行辨识。文献［10］中利用多层神经网络对采集到的电流和功率信息进行分析，实现负荷辨识。文献［11］中针对低频采样下的负荷特征问题，提出了一种可自动提取激活特征并识别类型的卷积神经网络（Convolution Neural Network，CNN）架构。文献［12］中将有功功率和无功功率作为训练数据训练K近邻（K-Nearest Neighbor，KNN）算法模型完成负荷辨识。文献［13］中提出了融合暂态电流波形和时域特征的改进方法，将暂态电流值均方根融合到电流波形图像以提升相似波形特征负荷的辨识正确率。文献［14］中结合居民用电行为与外部非电力负荷特征相关特性，建立一种基于随机森林的家庭负荷监测模型。文献［15］中将家电的运行电流数据转换成图片形式，建立了能够处理二维图像数据的卷积神经网络模型，达到了负荷辨识的目的。文献［16］中通过一维卷积神经网络（One-Dimensional CNN，1D-CNN）对时序特征进行提取，结合贝叶斯神经网络，对光伏出力进行时序预测。文献［17］中利用1D-CNN 对轴承故障特征随机信号进行特征提取，并对齿轮箱轴承故障进行辨识。文献［18］中建立1D-CNN 的钻杆故障诊断模型，根据钻杆的加速度信号对钻杆工作状态进行识别。1D-CNN 在训练过程中只利用了高级信号特征，对低级信号特征表现不足，如何自动全面地利用信号特征进行分类是一个研究难点。在实际应用中，由于受到存储技术的限制，在长期的负荷数据采样过程中无法实现实时高频采集，得到的负荷数据往往缺乏时序性。存储的数据量远远小于负荷正常运行时的数据量，由于负荷电流是随时间变化的，当负荷在某时刻发生投切，负荷状态不仅与当前时刻有关，还与其投切发生之前的状态信息有关，因此解决数据的时序性问题至关重要。

针对上述两个问题，本文提出了一种基于上采样金字塔结构的1D-CNN 非侵入负荷辨识算法，主要有三个关键部分：1）本文立足于实际应用场景，提出非侵入式负荷监测系统架构。该架构采用端侧数据采集，云侧模型训练，边侧模型部署结构，实现非侵入式负荷的快速辨识。2）针对一维向量型数据样本，在时间维度进行上采样，扩展数据在时间维度上的相关特征信息，解决采集数据时序性缺失的问题。3）利用双向金字塔结构对传统1D-CNN 进行优化，使得负荷特征利用更加全面，进一步提高算法的运行效率与准确率。所提算法在实验室中进行测试，验证其有效性。

1 上采样双向金字塔的1D-CNN原理

1.1 非侵入式负荷辨识原理

非侵入式负荷监测系统通过在用户电力入口处安装数据采集装置获取用户混合用电信息，并将采集到的混合信号分解为多个独立未知负荷信号，最终通过负荷辨识算法实现对未知负荷的识别，获取用户内部不同负荷的能耗信息与运行规律。由于该系统不需要在每一个负荷端口放置采集装置，安装成本大大降低，而且该系统不会对用户造成影响。

对于非侵入式负荷监测问题，传统机器学习模型虽然在处理时序负荷数据取得了较大的进展，但是将特征提取与分类作为两个独立部分进行处理，难以得出最优解。卷积神经网络通过卷积层自动提取负荷特征，全连接层实现负荷分类将特征提取与分类过程融合到一起，使得求最优解变得容易。传统CNN 与1D-CNN 的不同之处在于卷积核的尺寸不同。1D-CNN 在处理时序数据时无需将其转化为二维图像数据，对于处理一维时序数据更加适用，效率更高。如图1 所示，一维卷积核是通过卷积神经网络算法的不断迭代得到。利用最优一维卷积核，通过不断滑动对原始一维信号进行卷积运算，得到能够表征此类信号的时域特征。一维卷积核在运算过程中无需进行复杂的矩阵运算，产生的参数较少，能够在训练样本和迭代次数更少的情况下得到最优的结果。

端云协同的非侵入式负荷监测系统首先通过NILM 装置采集负荷独立运行的负荷信号，并通过通信网将数据传输到云端数据库进行储存。由于云端算力资源丰富，利用云端数据库对上采样金字塔结构的1D-CNN 算法进行训练，将训练好的算法利用通信网下发部署到端侧的设备中。在实际负荷监测过程中，通过采集混叠的负荷数据，结合负荷分解算法进行负荷分解，最后利用在端侧部署好的辨识算法实现负荷的快速辨识。图2 所示为非侵入式负荷监测系统。

1.2 双向金字塔结构

相较于辨识任务，卷积网络计算的特征提取方法逐渐取代传统机器学习的特征提取方法，由于卷积神经网络能够表示更高级别的负荷特征，不同层的特征尺度也不同，从而有助于从单一输出尺度上计算特征，但是这种做法的缺点在于只使用了高级分辨率特征，对低分辨率的特征表现不足。为了改善这种情况，在传统特征金字塔结构基础上增加递推的自底向上（Bottom-up）路径，有效地利用底层特征信息，使网络特征融合更加充分，大大减少了特征信息的损耗。具体双向金字塔结构如图3 所示。

Bottom-up 路径运算过程中三个相邻阶段特征图同时输入到模块中。第一个来自网络的较低层级，此特征图尺寸较大但通道较浅，具有丰富的细节信息，设特征图的尺度为H1×W1×C1。第二个特征图来自网络的中间层，此特征图尺寸和通道数都处于中间位置，设其特征图尺度为H2×W2×C2。最上层特征图来自网络的较高层，此特征图尺寸较小但通道较深，包含丰富的类别信息，设其特征图尺度为H3×W3×C3。三个特征图尺寸之间的关系为H1=2 ×H2，W1=2×W2，C1=2×C2，H2=2×H3，W2=2×W3，C2=2×C3。

具体融合过程如图4 所示。首先，低层级特征图输入到由5×5 卷积核组成的卷积层进行特征图调整，中层级特征图输入到3×3 卷积核组成的卷积层进行特征图调整，低层卷积层输出的特征图尺寸与高层级特征图尺寸对等；然后，中层级特征图与高层级特征图分别经过全局平均池化，1×1 卷积运算，并分别与5×5 卷积层处理过的低层特征图和3×3 卷积层处理过的中层特征图进行加权运算；最后，加权过的低层级特征图、中层级特征图和高层级特征图进行元素相加，完成最后的特征融合。

作为一种深度学习模型，卷积神经网络（CNN）广泛应用于图像识别、视频检测等领域，具有从复杂耦合的数据集中自动提取高级特征的能力，消除了传统方法中复杂的特征提取过程。CNN 的结构采用局部连接和权重共享的方法，大幅减小了网络参数的数量和降低了训练难度，显著提高了网络的泛化能力。在非侵入式负荷辨识问题中，由于采集的电压、电流信号为一维数据，将其转换成图像数据，耗时耗力不利于负荷的快速辨识。因此，本文提出一种用于特征提取的一维卷积层，与传统的二维卷积层相比，一维卷积层减少了参数数量，节省了负荷辨识的时间和存储空间。

2 上采样双向金字塔的1D-CNN算法

2.1 基于负荷数据时间维度的上采样

上采样需要对数字信号进行重采样，重采样的采样率与原来获得该数字信号的采样率比较，大于原信号采样率的称为上采样，上采样的实质也就是内插或插值。通过对负荷数据进行上采样处理，将负荷一维向量型数据升维成二维网格型数据，从而扩展负荷数据在时间维度上有价值的相关特征信息。

本文通过对独立负荷数据在时间维度上进行上采样，将负荷一维向量型数据升维成二维网格型数据，从而扩展负荷数据在时间维度上相关特征信息。该上采样网络结构主要包括输入层、重构层、时间上采样层，具体网络结构如图5所示。

重构层将输入层输入的负荷一维电流数据∈Rfr，重构成二维网格型数据，如式（1）～（2）所示，其中fI表示变量总数，使用Xi替代。

对于第TSj层的时间上采样层，根据式（3）对每个特征的时间序列进行全连接操作：

2.2 特征提取模块

对于特征提取模块，由3 个一维卷积（Conv1D）和3 个平均池化层级联构成，并采用双向金字塔形式设计模型中每层卷积核的个数。为更好地适应时序数据的矢量特性和加快卷积运算，采用一维卷积而不是二维卷积（Conv2D），Conv1D的输入和输出数据是二维的，而Conv2D 则应对三维输入输出，更适用于图像数据。Conv1D 主要通过数据与卷积核的卷积运算来提取数据高维特征，且卷积核的方向是Conv1D层输出的，如式（4）所示：

为降低下一层输入数据长度和扩大感受野的范围，使用平均池pool(·)来计算输入特征矢量的平均值，第l+1 层的第i个神经元平均池化输出为：

为了简化表示特征双向传递的过程，如图6 所示，虚线箭头表示低层和中层特征进行双向传播的过程，其中较长的虚线①代表低层级特征图传递到高层级的过程，较短的虚线②代表中层级特征图传递到高层级的过程。

2.3 分类器模块

从特征提取模块到分类器模块，需要采用Flatten 层将二维输出特征图展平压缩成一维特征矢量。分类器模块包括1 个全连接层和1 个输出层，其中输出层采用Softmax 激活函数，全连接层中采用ReLU 激活函数，神经元节点数为128，Flatten 层的输出数据为yl1，全连接层的输出特征矢量为：

其中：Wl2和bl2分别表示权重矩阵和偏置。Softmax 层将yl2转换为1×9 的概率矢量P=(p1，p2，…，p9)，对应识别9 种负荷概率，且概率之和为1，Softmax 层的第j个输出概率为：

2.4 网络优化

影响模型泛化性的主要因素是ReLU 函数在反向传播时会出现梯度消失、过拟合等问题，即模型在学习负荷特征的同时也会从数据中学习噪声或人为特征，因此，本文在模型中引入正则化处理，从而降低模型复杂度和不稳定程度，避免过拟合的问题。常用的正则化方法有L1 和L2 正则化，分别如式（8）～（9）所示：

L1 正则化：

L2 正则化：

相较于L1 正则化，L2 正则化具有处处可导、便于优化的特点，适合应用于本文提出的模型。因此，在更新卷积神经网络全连接层和Softmax 层的权值时加入L2 正则化。

2.5 模型评估

在实际的负荷辨识过程中“误判”对模型的整体性能影响较大；例如将电器A 误判成电器B、电器OFF 误判成ON时，导致用户实时掌握的负荷用电情况不够准确。本文采用2 个标准指标来评估模型的识别性能，分别为：准确率ACC（Accuracy）和F-score。准确率的计算公式如式（10）所示：

其中：真正例TP（True Positive）表示模型将正类预测为正类的样本数；假正例FP（False Positive）表示模型将负类预测为正类的样本数；真反例TN（True Negative）表示模型将负类预测为负类的样本数；假反例FN（False Negative）表示模型将正类预测为负类的样本数。

F-score可根据精确率P（Precision）和召回率R（Recall）计算得到，其中，精确率代表对正结果识别正确的数目在所有识别为正的结果中的比例，如式（11）所示；召回率则为对正结果识别正确的数目在所有正确识别结果中的比率，如式（12）所示。

F-score是对P和R的平衡，如式（13）所示：

3 实验与结果分析

3.1 非侵入式负荷数据采集系统及数据分析

为了验证本文算法的有效性，利用数据采集装置从实验室获取实际负荷的运行数据，构建测试数据集。该装置通过电压电流互感器将电压电流信号强度降低，并采用数据采集卡进行高频数据采集，最后将数据传输到服务器上进行后续处理。

具体实验参数为：采集装置接入电压220 V，采样频率10 kHz。辨识对象包括：电磁炉（Induction Cooker，IC）、电熨斗（Electric Iron，EI）、冰 箱（Refrigerator，RE）、电饭煲（Electric Cooker，EC）、电 视（Television，TV）、电水壶（Electric Kettle，EK）、电烤箱（Electronic Oven，EO）、饮水机（Water Dispenser，WD）和空调（Air-Conditioning，AC）。当上述负荷单独运行时周期电流信号如图7 所示。

本文以2∶1 的比例将样本集分为训练集和测试集，各子集通过均匀随机抽样从总样本集中取出。训练集用于对模型参数进行寻优，测试集用于验证模型的泛化性。双向特征金字塔多层卷积池化结构可提升网络性能，但是随着层数的增多，模型中的参数呈指数增长，极大地增加了模型复杂度。因此，本文根据样本长度、网络性能、模型复杂度，采用3 层卷积池化网络结构。

3.2 训练过程分析

首先，利用上采样网络对负荷的一维数据进行升维操作，将一维时序数据转化为二维网格数据再将网格型数据进行转置，并作为输入到双向金字塔神经网络中；然后，卷积层通过一系列的卷积核，对输入层的二维网格型数据进行扫描和运算，组合得到高维特征。如图8 所示，网络迭代到90 次以后，双向金字塔-1D-CNN 损失值趋近于最小，收敛速度较快；在迭代240 次以后传统的LeNet-1D-CNN［19］损失值才趋于最小，收敛速度相对较慢。通过对比可以看出，经过优化后的双向金字塔-1D-CNN 的损失值下降更快，在性能上优于传统的LeNet-1D-CNN。

为了更好地展示神经网络的内部参数，选取第2 个卷积层的权重Kernel-1 和偏差Bias-1 以及第3 个卷积层的权重Kernel-2 和偏差Bias-2 进行展示，如图9 所示，卷积核内部参数、偏置内部参数在迭代过程中逐渐收敛到稳定。进一步分析可以看出，当迭代到90 次左右时，各个参数相对趋于稳定，进一步说明本文算法在收敛速度、算法效率等方面优于传统的1D-CNN。

将最后输出的向量中数值作为判断负荷类别概率，输出的概率值保留小数点后2 位。如图10 所示，混淆矩阵的每一行代表了预测类别的概率，每一列代表了数据的真实类别。对角线上的值表示负荷被正确分类的概率，颜色越深代表概率值越大，作为此种负荷的可能性就越高。每个混淆对角线矩阵显示了9 类中每类负荷的预测精度。本文算法的识别精度较高，这意味着该算法可以学习更高级别和更多的特征，以提高预测性能。

为了验证本文算法的有效性，选取了以下4 种算法作为对比。

1）文献［20］中采用4 种负荷特征参数（电流、有功功率、无功功率、功率因素）作为算法的观测向量，通过算法学习和多次迭代得到多参数的隐马尔可夫模型（Multi-Parameter Hidden Markov Model，MPHMM），完成对负荷的最终辨识。

2）LeNet-1D-CNN 算法［19］首先是对传统的LeNet 神经网络卷积层进行降维，但在辨识阶段表现不是很好，主要原因是LeNet 神经网络在最初设计时适用于图像辨识领域。

3）文献［15］中利用局部平均分解算法对采集到的混合信号进行负荷分离，并提取独立负荷特征，建立了能够处理二维图像数据的卷积神经网络模型，该模型将一维电流数据转化为二维图像数据的过程繁琐，不能快速地进行负荷辨识。

4）文献［13］中提出了融合暂态电流波形和时域特征的改进方法，将暂态电流值均方根融合到电流波形图像中，该方法在文献［15］的基础上融合暂态特征，但是并没有解决数据转化繁琐、辨识效率较低的问题。

本文提出上采样双向金字塔卷积神经网络算法，通过上采样来弥补数据时序性缺失，结合上采样双向金字塔来优化传统LeNet-1D-CNN 结构。从图11 中可以看出，随着迭代次数的增加，5 种算法的识别准确率都在不断提高。但本文算法的准确率始终高于其他4 种算法。同时，在相同迭代次数下，其他评价指标的对比如表1 所示，从表1 中也可以看出本文算法的识别准确率达到了95.21%，F-score达到了94.93%，相较于对比算法，在准确率和F-score上都有优势。

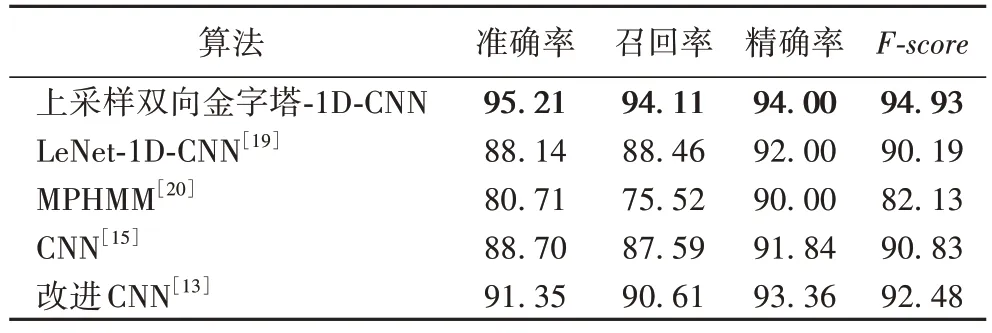
表1 不同算法的评价指标对比 单位：%Tab.1 Comparison of evaluation indexes of different algorithms unit：%

4 结语

本文立足实际情况，结合云侧算力资源丰富与端侧设备性能良好的优点提出了一种端云协同的非侵入式负荷监测架构；基于非侵入式负荷监测理论和卷积神经网络原理，结合负荷信号的一维特点与双向金字塔结构，提出了一种基于上采样金字塔结构的卷积神经网络非侵入负荷辨识算法。通过对原始单点一维向量型数据进行重构升维，在时序维度进行上采样，扩展负荷数据在时间维度上有价值的相关特征信息，来弥补数据时序性的缺失；通过双向金字塔来优化传统LeNet-1D-CNN 结构，增加网络对负荷低级特征的利用。实验结果表明，本文所提的上采样金字塔结构的1D-CNN 非侵入负荷辨识算法，在数据时序缺失的条件下，性能优于其他方法，提高了负荷辨识准确率，缩短了负荷辨识时间，进一步实现了负荷的实时监测。未来工作中将会进一步增加负荷类别，对算法进行优化以提高运行效率与准确率，实现负荷能耗的动态监测。