基于WiFi指纹序列匹配的机器人同步定位与地图构建

秦正泓，刘冉，肖宇峰，陈凯翔，邓忠元，邓天睿

（西南科技大学 信息工程学院，四川 绵阳 621010）

0 引言

近年来，同步定位与地图构建（Simultaneous Localization And Mapping，SLAM）逐渐成为机器人领域研究的热点问题，被认为是实现移动机器人自主化的核心技术［1-2］。Standford大学的Smith等［3］首先发表了关于SLAM 问题的开创性论文。针对SLAM 问题，国内外研究人员提出了很多解决方案，其中基于图优化的SLAM（Graph-based SLAM）把这一问题转化为最大似然估计，被认为是目前解决SLAM 最有效的方法之一［4-8］。闭环检测是实现图优化SLAM 的关键，也是SLAM 问题的一个难点。正确的闭环检测可以修正里程计的累计误差，从而得到一致性地图；错误的闭环检测结果则会对后续图优化造成干扰，导致地图创建的失败［9］。

目前进行闭环检测的主流方法是通过视觉（特征匹配）或激光（扫描匹配）。Ryu等［10］提出基于一帧激光数据与另一帧激光数据的扫描匹配算法（帧—帧），通过旋转和平移判断两帧激光数据的相似性，达到闭环检测的效果。Cho等［11］通过迭代最近点（Iterative Closest Point，ICP），获得一帧激光数据到另一帧的转换关系，通过判断相似性检测是否存在闭环。这种检测方法虽然能保证每帧数据都被检测到，但容易因局部相似性高产生错误的匹配结果和数据量的增多而延缓检测速度。Campos等［12］提出了一个相对完整的单目SLAM系统ORBSLAM（Oriented FAST and Rotated BRIEF SLAM）。该系统的各个线程均采用图像的ORB（Oriented FAST and Rotated BRIEF）特征，并引入本质图的概念来加速校验闭环检测，然而在此过程中需要提取大量的图像特征，计算量大，且在光线变化的情况下成功率较低。虽然通过视觉或激光来进行闭环检测的SLAM 方案已经非常成熟，但在大范围的复杂环境下，机器人所采集到的环境信息量庞大，对于激光传感器，大量的相似场景可能导致错误闭环的出现；对于视觉传感器，在光照多变和视野受限的条件下鲁棒性较低，且匹配算法复杂，计算开销巨大，从而大幅降低了图优化SLAM 的算法精度。因此，如何减小传感器匹配误差，提高SLAM 精度，是当前研究的重点之一。

早期的SLAM 研究是通过滤波实现机器人的状态估计。基于滤波器的方法主要是利用递归贝叶斯估计原理，在假定机器人所有时刻的观测信息以及控制信息已知的条件下，对系统状态的后验概率进行估计。根据后验概率表示方式的不同，常用的滤波方法包括扩展卡尔曼滤波器［13］、Rao-Blackwellised 粒子滤波器（Rao-Blackwellised Particle Filter，RBPF）［14］等。基于滤波器的方法存在更新效率低的问题，难以应用于大规模环境的地图创建［15-16］。

随着SLAM 的发展，基于滤波器的方法逐渐被基于图优化的方法取代。基于图优化的SLAM 方法采用了全局优化理论，能够获得更好的建图效果。Kschischang等［17］在2001年提出利用因子图对SLAM 问题进行建模。Carlevaris-Bianco等［18］提出了通过删除图的节点来降低后端优化计算的复杂性，节点被删除的顺序可能会影响图的连通性。Vallvé等［19］结合因子图建模与矩阵稀疏化理论，提出了节点下降优化方法，减少迭代的次数，但其收敛性不高，在大范围的复杂环境下表现较差。Golfarelli等［20］将基于图优化的SLAM 系统看作是质量—弹簧模型系统，将SLAM 问题转换为最小二乘问题；但当弹簧受力变形时，系统是不稳定的，且不适用于大范围的复杂环境。

虽然视觉传感器和激光传感器是SLAM 算法中最常用的两种传感器，但是这些设备往往价格比较昂贵，而且受周围环境变化的干扰较大。与激光传感器和视觉传感器相比，无线传感器在大范围复杂环境的情况下有更好的表现，其安装简便，价格便宜；并且，WiFi 的广泛普及给室内定位提供了新的机遇。市场上大量的移动通信设备（智能手机、笔记本电脑）都内嵌了廉价多样的传感器，例如WiFi 模块、运动传感器、全球定位系统（Global Positioning System，GPS）和摄像头等。而大部分室内环境都部署有WiFi 接入点（Access Point，AP），利用WiFi 进行SLAM 具有了很大的可行性。Ferris等［21］使用高斯过程潜变量模型将高维信号强度映射到二维空间，从而实现WiFi SLAM 的系统构建。Huang等［22］提出利用图优化SLAM 方法来解决WiFi SLAM 的问题，该方法通过高斯模型构建信号强度地图，但设备的差异以及应用环境的不同为高斯模型的建立带来了极大的困难。因此研究人员融合惯性测量单元（Inertial Measurement Unit，IMU）信息和指纹信息构建指纹地图，例如：Gu等［23］将脚戴式惯性定位系统与图优化SLAM 相结合进行指纹地图的构建；但该方法需要使用者在脚上单独佩戴IMU，不利于大范围的推广使用。Liu等［24］提出利用WiFi 指纹闭环和航位推算信息解决SLAM 问题；但运行时间较长时，航位推算与指纹闭环会出现不可避免的偏差。

针对大范围复杂环境下的图优化SLAM 问题，为提高指纹闭环的准确性，本文提出了基于WiFi 指纹序列匹配的图优化SLAM 算法。本文的主要工作如下：1）采用动态时间规划（Dynamic Time Warping，DTW）算法实现WiFi 指纹序列的匹配，保证了闭环检测的准确性；2）结合WiFi 指纹信息进行图优化SLAM，满足了SLAM 在大范围复杂环境下的算法精度要求。本文采用两组实验数据对算法进行验证，结果表明：与高斯相似度的方法相比，本文算法第一组数据的精度提高了22.94%；第二组数据的精度提高了39.18%。

1 算法设计

本文算法主要分为两部分：1）不确定性模型的生成；2）Graph-based SLAM 算法。整个算法的流程如图1 所示。

首先，利用高斯相似度来计算两个近距离指纹点的相似度，并通过一个训练过程来建立相似度和距离的不确定性模型；然后，计算两个远距离指纹点的相似度，如果其相似度大于某一阈值，得到一个高斯闭环，并将这两个指纹点作为两个指纹序列的起点，采用DTW 算法计算两个指纹序列的相似度，如果指纹序列的相似度满足一定阈值，再得到一个指纹序列的闭环；最后，将高斯闭环与指纹序列闭环作为约束加入到位姿图中，利用图优化算法对所构建的位姿图进行优化，得到优化后的机器人轨迹。

1.1 Graph-based SLAM算法

本文在未知环境中利用WiFi 数据进行SLAM，通过智能设备在运动过程中重复观测到的地图特征（WiFi 指纹）对自身进行定位。基于图优化的SLAM 从采集的传感器数据中构建一个位姿图，其中顶点表示位姿，边用于表示顶点之间的约束。约束分为两种：一种约束由连续时刻的里程计数据得到；另外一种约束可通过不同时刻观测数据的匹配得到（又称为闭环检测）。因为观测数据有一定的误差，所有的约束都附加有一个不确定性参数，由此将基于图优化的SLAM问题转化为寻找优化位姿使得约束带来的误差最小。

用(xt，yt)表示t时刻机器人的二维位置信息，θt表示方位信息。用C表示所构建约束的集合。Graph-based SLAM的目的是找到位姿的最佳配置，从而最小化以下函数：

其中：zij代表顶点i和j之间的刚体变换；Σ表示此变换不确定性的协方差矩阵。对于激光雷达，变换zij可以通过扫描匹配（例如ICP 算法）进行估算；对于视觉传感器，这一变换可以通过特征匹配来获取。给定某一AP 的接收信号强度（Received Signal Strength，RSS），可以很容易判定某一用户是否重新访问了某块区域，因为每个AP 具有唯一的硬件地址。但是通过信号强度估算两个测量点的相对位置关系则非常困难，因为RSS 本身没有包含任何距离或方向信息。

信号强度往往与距离有很大的关联，因此一些学者通过信号衰减模型来推算距离，典型的系统包括WiFi SLAM［25］和一些基于信号衰弱模型的室内定位系统。但是这一模型的获取非常困难，由于制造厂商的不一样，每一个AP 的参数都不一样；另外多径效应和环境中的物体对信号的传播都有很大的影响。使用位置指纹的方法来进行闭环检测可以克服环境对信号传播的影响，某个指纹点描述了在某一位置检测到的AP 以及对应的信号强度；就如人体的指纹和DNA（Deoxyribo Nucleic Acid）一样，WiFi 指纹可以作为特征用于唯一地描述某一位置，而两个位置的远近可以通过指纹点对的相似度来进行衡量。但在大范围的复杂环境下，仅仅采用指纹点对的匹配远远不够，由于高斯相似度计算方法只考虑了两个指纹点所扫描到的相同AP，因此可能导致指纹点对的匹配会出现闭环的误判（距离很近的两点但相似度却很低），将传统的基于指纹点对的匹配扩展到指纹序列的匹配，可以减小闭环误判的几率，从而确保算法的准确性。

1.2 WiFi指纹序列的匹配

由于指纹序列中包含多个指纹数据，信息量比单个指纹点对的数据丰富，所以，提出通过WiFi 指纹序列的匹配来进行闭环检测，利用DTW 算法实现两个指纹序列的闭环检测，在很大程度上可以减小定位误差。DTW 算法是一种弹性匹配算法，通过对两个指纹序列进行相互关系的搜索，运用动态规划思想调整两序列之间的对应关系，获取一条最优路径，使沿该路径两序列间的相似度最大。

首先采用高斯函数计算两个指纹点的相似度，将t时刻的指纹表示为Ft=(ft，xt)，其中xt=(xt，yt，θt)表示机器人在t时刻的里程计位姿；ft表示位置xt处采集的指纹信息。具体来说，指纹信息包括t时刻所扫描到AP 的硬件地址以及信号强度ft=(ft，1，ft，2，…，ft，Z)，其中Z表示t时刻扫描到AP 的数目。使用高斯函数来计算两个指纹点Fi和Fj的相似度：

如果两个指纹点的高斯相似度大于一定的阈值vs，将这两个指纹点作为两个指纹序列的起点，通过计算这两个指纹序列的相似度来进行闭环检测。假设两个指纹序列分别为L=l1，l2，…，ln和K=k1，k2，…，km，为了计算这两个指纹序列的相似度，首先是要找到两个序列之间的对应关系，以指纹序列L为横轴，指纹序列K为纵轴，构造一个n×m的相似度矩阵S，见式（3）。在相似度矩阵中，两个指纹序列存在多条对应的路径，以其中的一条为例，用黑点来表示该路径，如图2 所示，即W=w1，w2，…，wr-1，wr，wr+1，…，wR-1，wR，R表示路径W的长度，满足max(n，m) ≤R≤n+m-1；其中wk为该路径第r个点的坐标wr=(ir，jr)，它表示指纹序列L的第ir个指纹点与指纹序列K的第jr个指纹点相对应。则两点间的相似度可得两指纹序列所有对应点间的相似度矩阵S为：

相似度矩阵中的有效路径需满足以下约束条件，其约束条件示意图如图3 所示。

1）边界条件：起点为S(1，1)，终点为S(n，m)，也就是说，有效路径必定是从左下角出发，在右上角结束。

2）连续性：图3 中的路径从wr到下一点wr+1，需满足ir+1-ir≤1，jr+1-jr≤1。如图3 中的圆圈Ⅰ所示，为保证连续性，当沿该路径至点S(i，j)时，前一点须经过S(i-1，j-1)、S(i-1，j)、S(i，j-1)其中的一点，也就是说某个时刻的点只能和相同时刻以及相邻时刻的点匹配，无法跨越匹配，如图3 中的圆圈Ⅱ处所示。

3）单调性：从wr到下一点wr+1时，需满足ir≤ir+1、jr≤jr+1，这使得路径必须随着时间单调进行，不能出现时间上倒退的现象，如图3 中的圆圈Ⅲ处所示。

显然满足约束条件的有效路径W有多条，而DTW 算法需要寻找其中的最优路径，使沿该路径两序列间的相似度累计值最大。用Sseq(L，K)来表示指纹序列L和K之间的相似度，即最优路径所对应的相似度。Sseq(L，K)的求解过程为：

其中：r(i，j)表示在相似度矩阵S中从S(1，1)出发到S(i，j)路径上的相似度累计值；Sgauss(i，j)表示当前格点S(i，j)对应的高斯相似度Sgauss(li，kj)，也就是li和kj两指纹点间的高斯相似度。要到达点S(i，j)，只能从S(i-1，j-1)、S(i-1，j)或S(i，j-1)出发，max{r(i-1，j-1)，r(i-1，j)，r(i，j-1)}表示选择S(i-1，j-1)、S(i-1，j)和S(i，j-1)三点中相似度累计值最大的一个点作为出发点。重复上述过程，遍历整个相似度矩阵S，就可以找到一条从S(1，1)出发到S(n，m)的最优路径，最终得到r(n，m)的值，也就得到了指纹序列L和K之间的相似度Sseq(L，K)。

在求解Sseq(L，K) 之后，得到的最优路径用来表示，所以 两个指纹序列L和K之间的相似度可以表示为：

如果两个指纹序列的相似度值高于某一阈值vs，认为这两个位置是同一处，从而检测到了一个指纹序列闭环。然而，在实际过程中，这两个位置往往不可能在同一处，因此通过增加一个不确定性协方差参数来对这一误差进行补偿。不确定性协方差矩阵通常是一个对称矩阵，在实际的应用中可以选择一个数值很大的对角矩阵，对角阵元素的大小表明对这一误差的忽视程度。如果两指纹序列的相似度很高，并且对应的地面真实值小于3 m，表明两个指纹序列的实际距离很近，认为此时的误差很小，可以对其忽视，所以将对角阵元素设为1；由于将高斯闭环与指纹序列闭环都作为约束加入到位姿图中，所以对于高斯闭环与指纹序列闭环，把对角阵元素设为相似度样本方差的倒数。为了提高系统的精度，并且得到相似度样本的均值与方差，通过一个训练过程来建立相似度和距离的不确定性模型。

1.3 不确定性模型的训练

Graph-based SLAM 中的每一个边都需要指定其不确定性，对于里程计所构建的边，其不确定性可以由运动模型得到。为了提高系统的精度，通过一个训练过程来建立相似度和距离的不确定性模型。虽然里程计在长时间内会有累计误差，但里程计在短时间内是非常精确的，据所知一般里程计在30 m 的范围仍然很精确。因此计算所有距离小于30 m指纹的相似性，这样得到了H个训练数据表示两个指纹的相似度，dh表示两个指纹之间的距离。然后使用分箱方法（binning）来对样本进行训练，得到一个模型用于表示某一相似度对应距离的不确定性。也就是说，给定一个相似度S，计算与相似度S间隔为b的所有样本的均值与方差var(s)，通过均值与方差计算式（1）中的协方差矩阵Σ。

其中：c(b)统计相似度落在间隔b的样本的个数。通过此方法建立的不确定性模型可以参见图4。

2 实验与结果分析

为验证本文算法的性能，在新加坡南洋理工大学的2 号地下停车场（约5 100 m2）进行了两组实验。设计数据采集平台如图5 所示，选取机器人开发平台Clearpath Husky Automated Guided Vehicle 作为实验验证平台。机器人通过底盘得到里程计信息，数据采集频率设为10 Hz。在该机器人身上配置一个激光传感器Hokuyo UST-20LX 和5 个小米Max 3 智能手机，激光传感器用于实现自适应蒙特卡洛定位（Adaptive Monte Carlo Localization，AMCL），并将其所得姿态作为移动机器人在环境中的地面真实值；小米手机以0.5 Hz的频率采集WiFi 指纹数据。机器人从不同的起点开始，以0.4 m/s 的平均速度移动，共采集了两组实验数据。

在Graph-based SLAM中，不同的闭环检测方法对算法结果有很大的影响。本文以定位误差（即优化后的机器人轨迹与真实值的距离差值）衡量算法精度，定位误差越小，算法精度越高。首先，将指纹序列闭环的方法（n=20，m=25）与仅用高斯闭环的方法相比较，实验结果见表1。从表1 可以看出，vs太大或太小都会导致算法精度下降，对于不同的实验数据，其最适的相似度阈值也不同。当vs大于等于0.70时，系统还没有检测到闭环，导致其误差较大，都为18.99 m（第一组数据）和10.12 m（第二组数据）；当vs=0.10时，第一组数据的SLAM 算法精度最高，可以达到3.23 m；当vs=0.20时，第二组数据的SLAM 算法精度最高，可以达到2.67 m。然后，将高斯闭环与指纹序列闭环都作为约束加入到位姿图中，使用该方法所得结果：第一组数据为3.09 m，与仅使用高斯的方法（精度为4.01 m）相比提高了22.94%；第二组数据为2.36 m，与仅使用高斯的方法（精度为3.88 m）相比提高了39.18%。

为了验证实验环境在受到干扰之后其算法精度是否会受到影响，对原始的WiFi 信号强度加了3 种干扰：1）在原本所扫描到的AP 基础上删除某部分AP，实验一共采集了8 614 个指纹点，每个指纹点所扫描到AP 的个数在（40，130），所以在每个指纹点所扫描AP 中随机删除5 个AP；2）对信号强度增加方差为3 的高斯噪声；3）对信号强度增加方差为5 的高斯噪声。实验结果见表1，在3 种干扰情况之下，第一组实验数据得到的最优SLAM 算法精度为3.35 m、3.02 m 和3.11 m，第二组实验数据得到的最优SLAM 算法精度为2.74 m、2.41 m 和2.61 m。实验结果表明，整个SLAM 算法在环境受到干扰的情况下，其稳定性较高，虽然对原始的WiFi 数据（信号强度、AP 的数目）做了一定的处理，但因为后期有可靠的指纹闭环检测对数据的偏差进行消除，再加上图优化算法对机器人的轨迹进行优化，所以整个SLAM 算法的适用性和稳定性得到了验证。

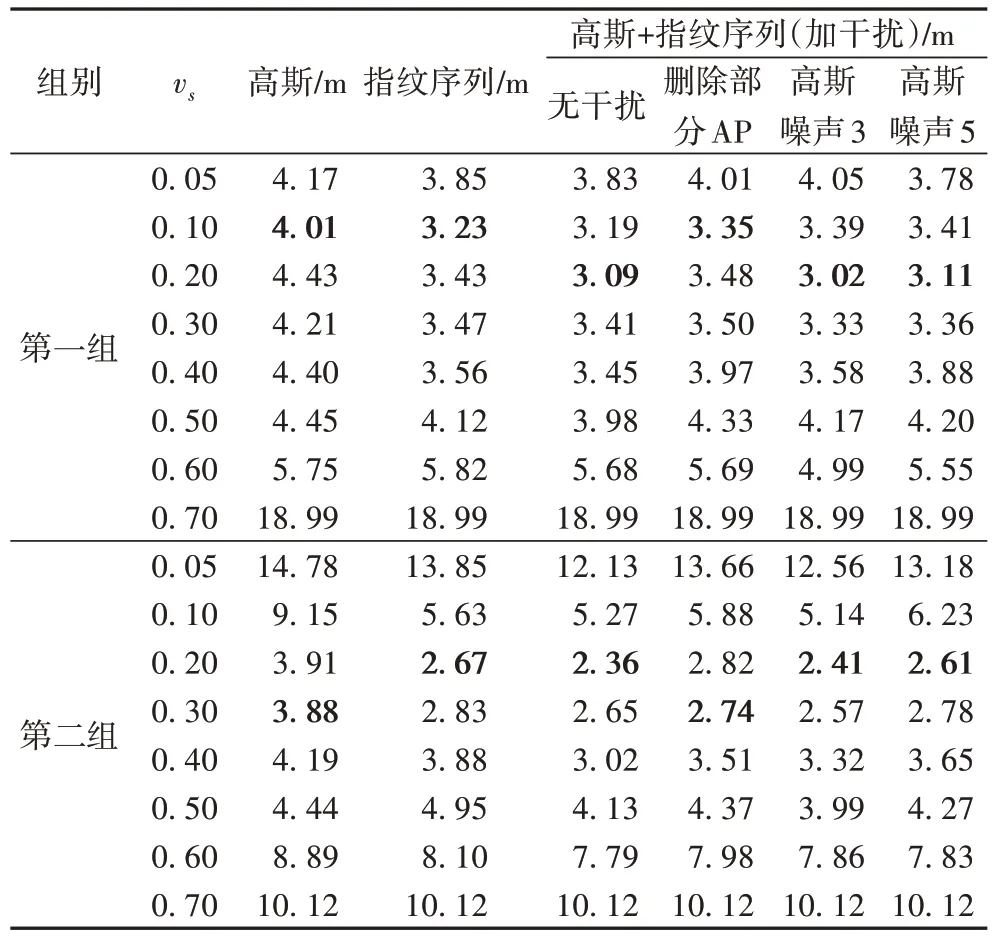
表1 不同的闭环检测方法与vs对SLAM算法精度的影响Tab.1 Influence of different loop closure detection methods and vs on SLAM algorithm accuracy

从表2 可以看出，指纹序列对应的闭环数目少于高斯对应的闭环数目，这是由于指纹序列包含了多个连续指纹点，原来的单个指纹点即可组成一个闭环，而现在需要多个指纹点才能组成一个闭环，也就导致算法得到的闭环数量大大减少，因此加入位姿图中的“指纹-闭环”边也就更少。并且，相似度阈值vs也对闭环数据有一定的影响，相似度阈值vs越小，闭环数目越多，相似度阈值vs越大，其闭环数目也越少，当相似度阈值vs大于等于0.70时，系统检测不到闭环，所以闭环数目为0。

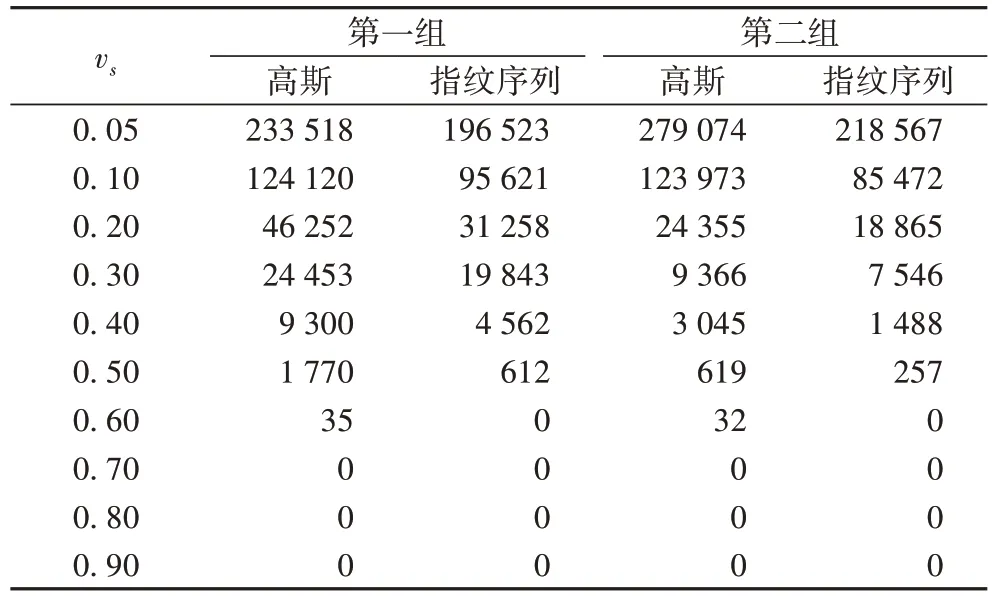
表2 不同的闭环检测方法与vs对闭环数目的影响Tab.2 Influence of loop closure detection methods and vs on loop closure number

换言之，运用指纹序列的方法，通过减少闭环数目来减小闭环误判的几率，从而保证了图优化结果的正确性。如图6所示，将优化后的机器人轨迹与地面真实值作对比，通过两组实验数据的结果可以看出优化后的机器人轨迹与地面真实值基本一致。其中高斯+指纹序列与地面真实值最接近。

除此之外，还研究了指纹序列的长度对所提算法精度的影响。采用高斯+指纹序列的方法，分别取5 组数据，其对应的结果如表3 所示，从表3 数据可以看出，当n=20且m=25时，其算法精度最高。当指纹序列太短时，因为其包含的指纹信息量不够，导致闭环检测不准确。当指纹序列的长度太长时，由于指纹数据量太大会增加计算复杂度，从而导致SLAM 算法精度降低。在对实验数据加3 种干扰的情况下，第一组实验数据得到的最优SLAM 算法精度为3.29 m、3.02 m 和3.11 m，第二组实验数据得到的最优SLAM 算法精度为2.74 m、2.39 m 和2.58 m。实验结果表明，优化后的算法在受干扰的情况下的稳定性较高，虽然最优算法精度对应的序列长度值有所变化，但与基于单个指纹点的高斯方法相比，仍然有很大提高。

表3 高斯+指纹序列方法下指纹序列的长度对SLAM算法精度的影响 单位：mTab.3 Influence of length of fingerprint sequence on SLAM algorithm accuracy under Gauss+fingerprint sequence method unit：m

3 结语

本文提出了基于WiFi 指纹序列匹配的图优化SLAM 算法。首先在机器人上搭载小米手机采集WiFi 指纹信息，通过DTW 算法实现指纹序列的闭环检测，然后将高斯闭环和指纹序列的闭环都作为约束加入到位姿图中，并通过图优化算法对机器人的轨迹进行优化，最后得到优化后的机器人轨迹。通过两组实验数据对所提算法进行了验证，定位精度均有很大提高，分别可以达到3.09 m 和2.36 m，与仅使用高斯的方法相比提高了22.94%和39.18%。可以明显看出，本文算法在大范围复杂环境下极大地提高了SLAM 精度。在后续的研究工作中，考虑加入其他传感器信息的融合获取更高的定位精度。