评价生物类似药分析相似性的质量范围法研究

吴克坚，王 陵，李 晨，夏结来

(空军军医大学：1基础医学院数学物理教研室， 2军事预防医学系军队卫生统计学教研室，陕西 西安 710032)

近年来，以原研生物药为基础开发的生物类似药进入了发展快车道，迎来研发热潮。由于生物制品具有分子量大、复杂的结构和生产工艺等特点，生物类似药的研发通常采用逐步递进的顺序分阶段进行候选药与参照药的相似性评价。质量属性的分析相似性研究是研发的必经之路，是简化临床前研究和临床研究的基础。美国食品药品监督管理局(Food and Drug Administration，FDA)2017年9月发布了《评价分析相似性的统计方法》[1]，提出对高、中、低三个风险层级的关键质量属性(critical quality attributes，CQAs)分别采用等效性检验法、质量范围法、图谱对比法进行评价。国内外学者围绕这些方法尤其是等效性检验进行了详细的讨论，并做了模拟和实例研究[2-7]。2018年6月，综合各方意见后美国FDA撤销了该指南草案，但其思想仍具有非常强的指导意义。

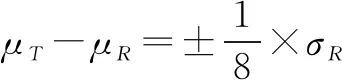
1 方法

首先简要介绍等效性检验方法，其次详细说明确定乘数k的方法与步骤。

1.1 第一层级CQAs的等效性检验方法

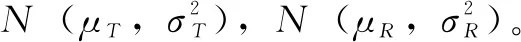
H0:μT-μR≤ΔLorμT-μR≥ΔU

H1:ΔL<μT-μR<ΔU

(1)

并且，若下式成立，则拒绝上述原假设H0

(2)

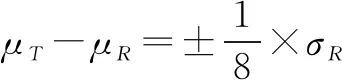
此外，在SHEN等[13]研究的基础上还得到了等效性检验的效能[7]：

(3)

1.2 产生与等效性检验的效能对应的乘数

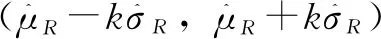
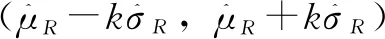
①设定α,σR/σT,θ,f，其中差异θ的变化范围是[-fσR,fσR]。按照公式(3)编写程序可得到不同θ对应的检验效能，以效能≥80%为分界点将区间[-fσR,fσR]分成3个部分：[-fσR,θEQ1)，[θEQ1,θEQ2]及(θEQ2,fσR]，其中[θEQ1,θEQ2]是候选药与参照药具有分析相似性的等效区间。

②当μT-μR在区间[θEQ1,θEQ2]变动时，设定质量范围的覆盖率为cEQ=0.9，即候选药与参照药两者相似时，质量范围包含候选药90%的质量属性分析值。这种设置将等效区间与质量范围法的覆盖率联系起来。

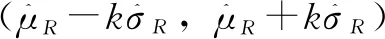
④为了便于操作且保证乘数k在整个等效区间[θEQ1,θEQ2]上的适用性，最终的乘数统一确定为kTier 1=max(k1,k2,…,kn)。

2 模拟与结果

2.1 不同等效界值对应的效能曲线

设定检验水准α=0.05，nT=nR=10，σR=1，σR/σT=1，图1给出了不同界值对应的等效性检验效能曲线。结果显示，6条效能曲线均关于μT-μR=0左右对称。当μT-μR=0时检验效能最高，μT-μR=±fσR时效能接近检验水准0.05。f越大，其对应的等效区间越宽。当f=1.5时，等效区间为[-0.32σR,0.32σR]。

2.2 第一层级CQAs质量范围法的乘数kTier 1

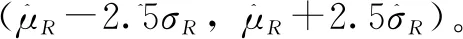
2.2.1 模拟3种场景下通过等效性检验和质量范围法的百分比

场景1：nT=nR=10，σR/σT=1，μT-μR的变化范围为[-1.5σR,1.5σR]；

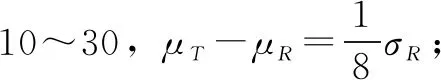
场景3：σR/σT=1，nT=nR且变化范围为10～30，μT-μR=1.5σR。

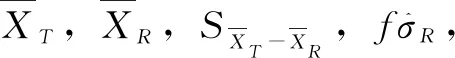
场景1的模拟结果见图2。由图2可知，样本XR,i,XT,i支持等效性与通过质量范围法的两条百分比曲线在整个μT-μR的变化区间内(图2中竖直虚线范围表示等效区间)是关于μT=μR对称的。同时，通过质量范围法的百分比始终高于等效性检验的百分比，这是由于等效性检验比质量范围法更为严格。

2.2.2 3种场景下4个概率值的估计曲线 为进一步考察等效性检验和质量范围法的关系，定义如下4个概率：p11表示同时通过等效性检验和质量范围法的概率；p12表示通过等效性检验但不能通过质量范围法的概率；p21表示不能通过等效性检验但通过质量范围法的概率；p22表示均不能通过等效性检验和质量范围法的概率。由于等效性检验比质量范围法更为严格，因此p12的估计值应该很小。

按照前述步骤分别计算3种场景下4个概率的估计值。图5给出了场景1的4个概率值估计曲线：p11的估计曲线似钟型，关于μT=μR对称，且在μT-μR=0处最大，两边呈下降趋势，与检验效能曲线类似；p12几乎为0，表示乘数kTier 1=2.5能保证若通过等效性检验则可通过质量范围法；p21的估计曲线在等效区间内下凸，即不能通过等效性检验的概率较低，在等效区间外侧呈逐渐增大趋势，表示通过质量范围法的概率较大；p22的估计曲线整体呈下凸形，在等效区间内等效性检验与质量范围法均不通过的概率控制在10%以内。

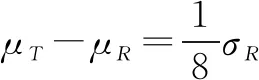
2.3 第二层级CQAs质量范围法的乘数kTier 2

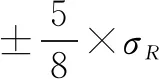
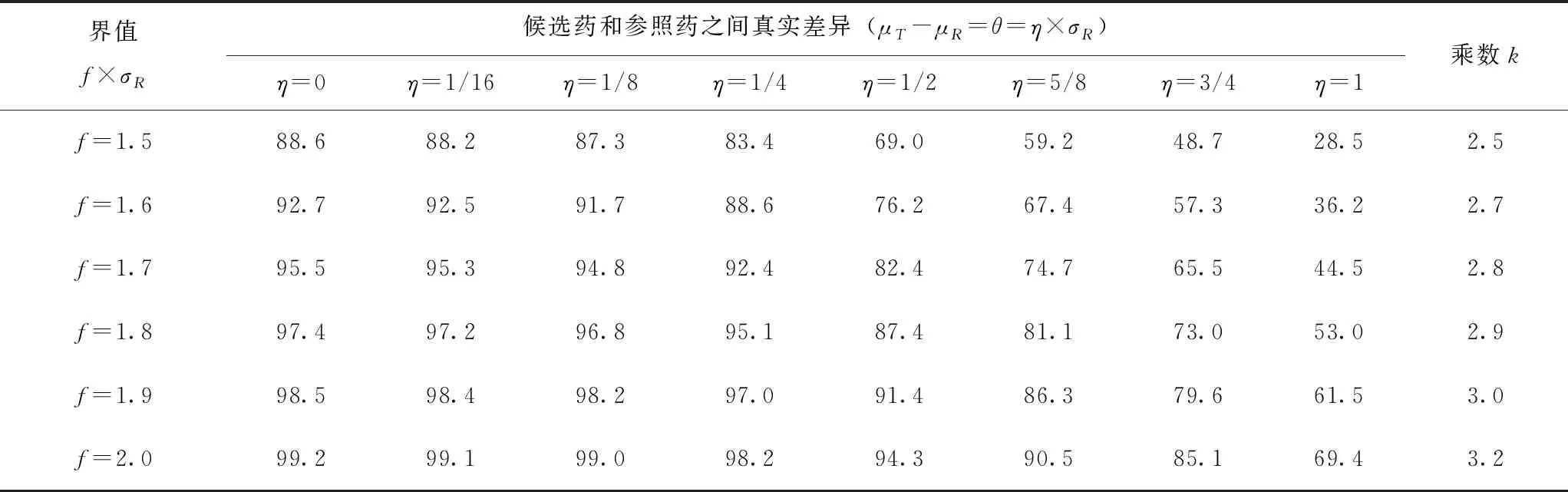
表1 固定nT=nR=10不同差异、不同界值分配的检验效能 (%)

3 实例应用

本实例应用中第一层级的质量属性数据分别来源于文献[16-17](表2)。对于质量属性1，有nT=

表2 质量属性1和2的分析测试值

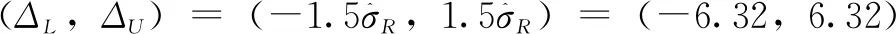
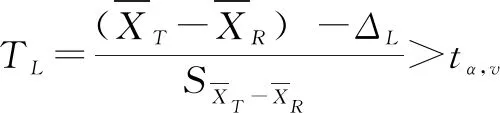
所以作出推断：候选药与参照药的质量属性1具有分析相似性。类似地可推断：候选药与参照药的质量属性2不具有分析相似性。需要指出的是，QUIROZ等[18]提到的由广义置信区间法、Howe法等推断相似性也能得到一致的结论。

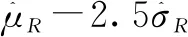
4 讨论

本文在等效性检验效能精确公式的基础上，得出第一层级CQAs质量范围法的乘数kTier 1=2.5，第二层级CQAs的乘数kTier 2=3。并且，设置3个场景、4个概率值解释了乘数的合理性。需要说明的是，在本文“方法”部分所述的步骤③中，我们计算了一组百分比数据的第10百分位数P10，并在后续的模拟研究中验证了由此得到的乘数k是合适的。我们还做了很多尝试，如：①若计算这组百分比数据的第1百分位数P1，则得到kTier 1=3.9；②若计算这组百分比数据的第5百分位数P5，则得到kTier 1=3。P1,P5及P10这些统计量作为位置指标，位置越靠前对应的乘数就越大。因现有文献通常将k=3定为第二层级CQAs质量范围法中的乘数，故本文最终选取P10统一计算乘数。

质量范围法非常容易实施，可帮助试验者快速做出决策，仅考查候选药组90%以上的分析值是否落在参照药的质量范围内即可。对于第一层级CQAs的相似性评价优先推荐更严格的等效性检验，其次为kTier 1=2.5的质量范围法；对于第二层级的CQAs推荐kTier 2=3的质量范围法。无论是等效性检验还是质量范围法，都应纳入尽可能多批次的参照药与候选药(如10批次以上)，如此分析结果才具有统计学意义。