自动实现G1连续的组合曲线曲面构造方法
魏子华,严兰兰
(东华理工大学理学院,330013,南昌)
0 引言
Bézier方法是现代计算机辅助几何设计(CAGD)中使用最广的方法之一,它能够受到如此广泛的应用得益于自身的诸多良好性质,例如端点插值、对称性、几何不变性与仿射不变性、凸包性等,而它的诸多良好性质都归功于Bernstein基函数优秀的代数性质。尽管Bézier方法有诸多便捷之处,但它在曲线曲面形状调整方面仍然存在不足,要想调整曲线曲面的形状就只有改变控制顶点的位置,这给计算带来不便的同时还可能会违背设计者的意图。另外,单一的Bézier曲线曲面要想表示较为复杂形状就只能提高其次数,但由于Bézier方法具有整体控制却缺乏局部调整的性质,任何局部的修改都会牵一发而动全身,所以在实际运用中Bézier曲线曲面的次数超过10次是禁忌的[1]。因此为了满足工业生产对于描述复杂形状的需求, 往往会采取Bézier曲线曲面组合拼接的方式, 拼接时需要考虑光滑度的问题。对于G1连续,除了需要满足位置连续以外,还需要满足3个控制顶点共线, 对此需要通过一定的计算来选取合适的控制顶点。相邻曲线拼接若要满足较高光滑度则需要满足较为复杂的条件。
对于Bézier方法在曲线曲面形状调整方面的不足,已有许多文献提出了解决办法,这类文献大多是构造含参数的基函数,使其定义的曲线曲面具有类似Bézier曲线曲面的诸多良好性质,且能通过调整形状参数值来调整曲线曲面的形状。有的学者在代数多项式空间中对Bézier方法进行改进,例如,王海波等[2]由三次Bernstein基函数扩展定义了一种带2个形状参数的四次多项式基函数;Hu Guang等[3]由n次Bernstein基函数定义了带n个形状参数的n次多项式基函数(n≥2);李军成等[4]利用递推性质定义了带2个形状参数的n次曲线(n≥3),对同次Bézier方法进行了扩展;除此之外,文献[5-7]都是在代数多项式空间上对Bézier方法进行改造。也有学者在非代数多项式空间中对Bézier方法进行改进,例如,张贵仓等[8]在三角函数空间定义了带4个参数的三次多项式曲线;Hu Guang等[9]在双曲函数空间定义了带4个参数的四次多项式曲线曲面;TAN X W等[10]在三角函数空间定义了带2个参数的五次多项式曲线;除此之外,文献[11-14]也是在非代数多项式空间进行Bézier方法的扩展。还有学者同时在代数和非代数多项式空间对Bézier方法进行扩展,例如,王成伟[15]以三次Bernstein基函数和二次三角Bézier型曲线的基函数为工具构造了一组带3个参数的三次基函数;Zhu Yuanpeng[16]等将代数多项式空间的三次Bernstein基函数与指数函数相结合, 构造了一组带2个参数的三次基函数;拓明秀[17]等将代数多项式空间的三次Bernstein基函数和三角多项式空间的三次类Bernstein基函数相结合构造了一组带3个形状参数的三次基函数。从代数多项式空间进行Bézier方法扩展,计算简单但不能很好地表示圆锥截线,在非代数多项式空间进行Bézier方法扩展,不便于计算但能更好地表示圆锥截线。
文献[2-17]所定义的曲线曲面,不仅保留了Bézier曲线曲面的诸多良好性质,而且能够在不改变控制顶点的前提下,通过调整形状参数来达到改变曲线曲面形状的目的。但这些文献鲜有考虑拼接方法的难易性,其中的曲线曲面拼接往往需要较为复杂的条件以实现较高阶的几何连续性或者参数连续,在实现低阶连续时也并未给出比Bézier方法更为简便的拼接条件。
工业生产中对于光滑度要求较低的生活物品的制造,往往不需要高阶连续,G1连续足以满足需求。为了能在简单条件下实现G1光滑拼接,这里定义了一类n(n≥2)次曲线,它们都可以在不改变控制顶点的情况下,通过改变参数值达到调整首、末端点位置的目的,当n≥4时还可以通过调整参数值自由调整曲线内部形状。同时定义了对应的曲面,它们和曲线一样,也可以通过调整形状参数值达到调整形状的目的。曲线拼接时,只需第1段曲线控制多边形的最后一条边与第2段曲线控制多边形的第1条边重合、且两参数之和为1,即可实现G1连续,同理对应的曲面也可以在简单的条件下实现G1光滑拼接。
1 基函数的构造及其性质
定义1:对于任意t∈[0,1],参数α,γ∈[0,1)、β∈(0,1],称如下函数组为带3个参数的n阶Bernstein基函数,简称n阶αβγ-B基。
当n=2时,称t的二次多项式
(1)
为2阶αβγ-B基;
当n=3时, 称t的四次多项式
(2)
为3阶αβγ-B基;值得注意的是,当n=3时t的三次多项式同样存在,t的三次多项式为
由于n=3时的四次多项式更符合不同阶αβγ-B基的构造方式,且能更精确地表示图形,同时为在后文的证明及拼接不引发歧义,故n=3时都采用t的四次多项式。当n为偶数且n≥4时,称t的n+1次多项式
(3)
为n阶αβγ-B基;当n为奇数且n≥5时称t的n+1次多项式

(4)

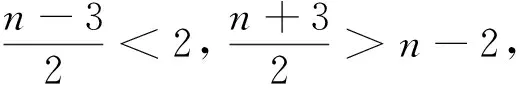
下面用Bernstein基函数来表示n阶αβγ-B基,其中当n=2时
(5)
当n=3时
(6)
当n为偶数且n≥4时
(7)
当n为奇数且n≥5时
(8)
由定义容易得到αβγ-B基的如下性质。
1)非负性:当参数α,γ∈[0,1),β∈(0,1]时,对任意t∈[0,1]都有fn,i(t)≥0(n=2,3,4,…, 0≤i≤n)。
证明:由Bernstein基函数的非负性以及参数范围容易得到式(5)~式(8)中fn,i(t)≥0(n=3,4,…,0≤i≤n)。
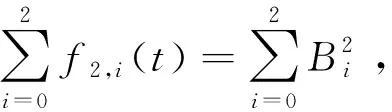
3)对称性:对任意t∈[0,1],当α=γ时,有fn,i(t)=fn,n-i(1-t)。
证明:由式(5)~式(8)及Bernstein基函数的对称性易知。
4)端点性质:对n=2,3,4,…,0≤i≤n,αβγ-B基在端点处的函数值如下
(9)
当n=2时αβγ-B基在端点处的一阶导如下:
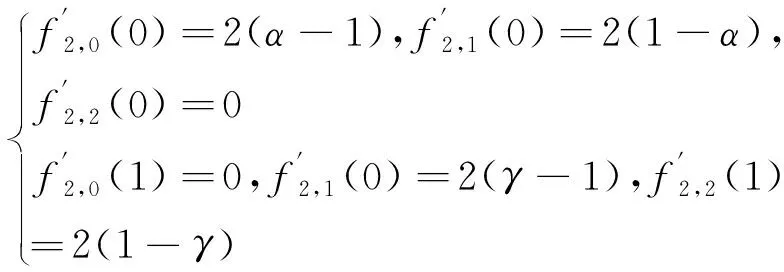
(10)
当n=3,4,…, 0≤i≤n时αβγ-B基在端点处的一阶导如下:
(11)

证明:假设
(12)
其中kn,i∈R。
①当n=2时,将式(5)代入式(12)中,整理得
由二次Bernstein基函数的线性无关性可知
k2,0(1-α)+k2,1α=0;k2,1=0;k2,1γ+k2,2(1-γ)=0
易得此方程组的解为k2,i=0(i=0,1,2)。
②当n=3时,将式(6)代入式(12)中,整理得
由四次Bernstein基函数的线性无关性可知
易求得此方程组的解为k3,i=0(i=0,1,2,3)。n≥4时同理可证。
2 曲线及其应用
2.1 曲线的定义及性质
定义2:给定n+1个控制顶点Pi∈d(d=2,3, 0≤i≤n,n≥2),参数α,γ∈[0,1),β∈(0,1], 对任意t∈[0,1],定义曲线
为n阶αβγ-Bézier曲线。
αβγ-Bézier曲线具有如下性质。
1)端点性质:由αβγ-B基的端点性质,可以推出对于n=2,3,4,…,0≤i≤n,αβγ-Bézier曲线的端点位置如下
(13)
当n=2时,αβγ-Bézier曲线的端点导矢如下
(14)
当n=3,4,…, 0≤i≤n时,αβγ-Bézier曲线的端点导矢如下
(15)
2)几何不变性:由αβγ-B基的规范性可知,αβγ-Bézier曲线的形状不依赖坐标系的选取。
3)凸包性:由αβγ-B基的规范性和非负性可知,αβγ-Bézier曲线rn(t)恒位于由控制顶点Pi(0≤i≤n,n≥2)确定的凸包中。
4)形状可调性:在不改变控制顶点位置的条件下,调整αβγ-B基中的任意参数值,都能改变αβγ-Bézier曲线的形状,其中调整参数α会影响曲线的起点位置,调整参数β不会影响曲线起点和终点的位置但会改变曲线内部形状,改变γ会影响曲线的终点位置(见图1~图3)。

图1 仅改变参数α

图2 仅改变参数β
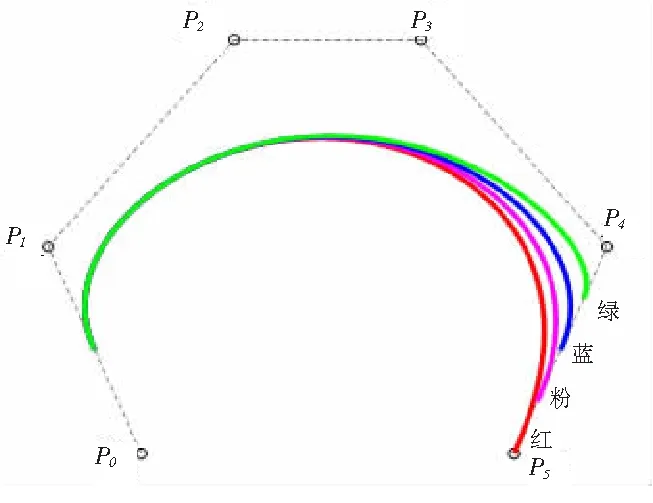
图3 仅改变参数γ
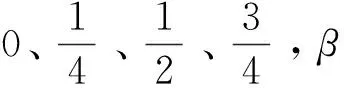
从图1可以看出仅改变参数α时曲线的起点位置会发生改变,α越小起点越靠近首个控制顶点,当α=0时曲线首端与首个控制顶点重合;从图2可以看出仅改变参数β时曲线的起点和终点位置不发生改变,但曲线形状会改变;从图3可以看出仅改变参数γ时曲线的终点位置会发生改变,γ越小终点越靠近最后一个控制顶点,当γ=0时曲线末端与最后一个控制顶点重合。
5)对称性:由αβγ-B基的对称性知,当α=γ时,控制顶点Pi(i=n,n-1,…,0;n≥2)和Pi(i=0,1,…,n;n≥2)定义的αβγ-Bézier曲线具有相同的形状。由图1~图3易知。
2.2 曲线的G1拼接条件
由于G1连续条件对于曲线而言要求不高,在低阶曲线上的适用性更强,故先讨论所构造的低阶曲线拼接条件。


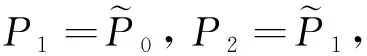
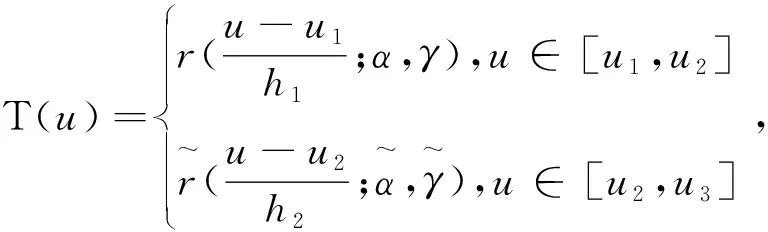
(16)
其中,h1=u2-u1,h2=u3-u2。
由式(13)、式(16)可知
(17)
由式(14)、式(15)及式(16)可知
(18)
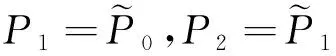
即满足G1连续条件,故曲线T(u)在公共连接点处G1连续。虽然低次曲线G1连续拼接更有意义,但任意次曲线的G1连续拼接能为工业生产制造提供更多选择,故下面讨论任意次曲线的G1拼接条件。
设有m条大于等于二阶的αβγ-Bézier曲线段
其中j表示曲线段的序号,第j条曲线的阶用nj表示,Pj,i表示第j条曲线的第i+1个控制顶点,αj,βj,γj表示第j条曲线段的参数,其中二阶和三阶αβγ-Bézier曲线段中不含参数β,在运用时注意省略。j=1,2,…,m,0≤i≤nj,m≥2,nj≥2,t∈[0,1],αj,γj∈[0,1),βj∈(0,1]。
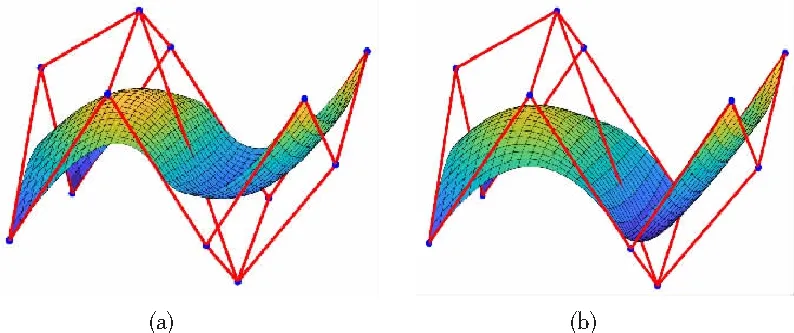
定理1:给定节点向量u1 (19) 其中hj=uj+1-uj,j=1,2,…,m。 若这m条曲线段的控制顶点和形状参数满足条件 (20) 则曲线R(u)在公共连接点处G1连续。 证明:由式(13)及式(19)可知 (21) 当nj-1=nj=2时,由式(14)及式(19)可知 (22) 当nj-1=2,nj≥3时,由式(14)、(15)及式(19)可知 (23) 当nj-1≥3,nj=2时, 式(14)、(15)及式(19)可知 (24) 当nj,nj-1≥3时,由式(15)及式(19)可知 (25) 要使曲线R(u)在公共连接点处G1连续,需满足 (26) 给定m条大于等于二阶的αβγ-Bézier曲线段,假设所要构造的组合曲线是由这m条曲线段组成的。由2.2节中约定的记号可知,组合曲线的首、末两端控制顶点分别为P1,0和Pm,nm,每段曲线的内控制顶点为Pj,i(j=1,2,…,m, 0≤i≤nj),由定理1可知只要控制顶点满足Pj-1,nj-1-1=Pj,0,Pj-1,nj-1=Pj,1,参数满足αj=1-γj-1,组合曲线在公共连接点处就满足G1连续,其中j=2,3,…,m。 注:要想构造封闭的组合曲线,除了满足上述要求,还需满足Pm,nm-1=P1,0,Pm,nm=P1,1,α1=1-γm,以此保证组合曲线首尾相接且在连接处G1连续。 图4~图6为用上述方法构造的组合曲线,其中空心圆点代表控制顶点,星号表示分段连接点。 图4 插值于首、末端点的G1连续开曲线 图5 G1连续闭曲线 图6 未插值于首、末端点G1连续开曲线 由图4~图6可见不同次数的αβγ-Bézier曲线可以自由拼接,拼接时能够在不改变控制顶点的前提下,通过改变其中的形状参数局部调整曲线形状。从图4和图6中可以看出组合αβγ-Bézier曲线可以插值于首、末端点,也可以不插值于首、末端点,这取决于第一段的参数α和最后一段的参数γ取何值。 众所周知G1拼接涉及到第1段曲线的后2个控制顶点和第2段曲线的前2个控制顶点,G2拼接涉及到第1段曲线的后3个控制顶点和第2段曲线的前3个控制顶点。对于高阶曲线而言G2连续是比G1连续更好的连续性选择,但所需满足的条件也随之提高。下面将讨论2条三阶αβγ-Bézier曲线的G2连续拼接条件。 设有2条三阶αβγ-Bézier曲线段 给定节点u1 (27) 其中,h1=u2-u1,h2=u3-u2。 给定定理1中的条件,由式(13)、式(27)可知 (28) 由式(15)、式(27)可知 (29) 由式(2)可知三阶αβγ-B基在端点处的二阶导如下 可推知三阶αβγ-Bézier曲线在端点处的二阶导如下 (30) 要使得组合曲线在拼接点处G2连续,则需要满足 (31) 由组合曲线满足定理1中给定的预处理条件可知T(u)在拼接点处G1连续,即满足式(31)中的条件(a)、(b),只需要再满足式(31)中的条件(c),组合曲线T(u)在拼接点处就能够达到G2连续。 (32) 即对于任意的参数λ2而言,只要控制顶点满足式(32),组合曲线就能达到G2连续。 定义3:给定(m+1)×(n+1)个控制顶点Pij∈3(i=0,1,…,m,i=0,1,…,n,m,n≥2),参数α1,γ1,α2,γ2∈[0,1),β1,β2∈(0,1],对任意u,v∈[0,1],定义曲线 为m×n阶αβγ-Bézier曲面。 αβγ-Bézier曲面具有与αβγ-Bézier曲线类似的性质,例如几何不变性、对称性、形状可调性、凸包性等。下面给出αβγ-Bézier曲面的拼接条件及证明。 定理2:设有若干个m×nk阶的αβγ-Bézier曲面 (33) (34) 则曲面p(u,v)在公共连接线处G1连续。 证明:由式(9)、式 (33)可得 (35) 由式(10)、式(35)可知,当nk=2时,有 (36) 当nk-1=2时,有 (37) 由式(11)、式(33)可知,当nk≥3时,有 (38) 当nk-1≥3时,有 (39) 若阶为m×nk-1的曲面与阶为m×nk的曲面满足 (40) 则组合曲面在拼接处G1连续。 图7 G1连续组合曲面 本文定义了n阶αβγ-Bézier曲线,并将其推广至曲面,定义了m×n阶αβγ-Bézier曲面。该曲线具有Bézier曲线的诸多良好性质,且能够在不改变控制顶点的情况下通过调整参数改变形状。二阶和三阶αβγ-Bézier曲线在端点处可调,更高阶的曲线在端点处及内部都可调,同时αβγ-Bézier曲线的G1拼接条件非常简便。但是由于提高二阶Bézier曲线的次数会使得参数的选取范围受限,影响其他次数的曲线构造,因此构造二阶αβγ-Bézier曲线曲面时相对于二阶Bézier而言并未提高次数。G1连续是工业设计中较为实用的一种连续条件,能满足大多数简单工艺生产的需求。本文给出的曲线曲面既能比Bézier曲线更易于实现G1连续拼接,而且能实现在不改变控制顶点的前提下自由调整形状的目标,因此使用更加方便。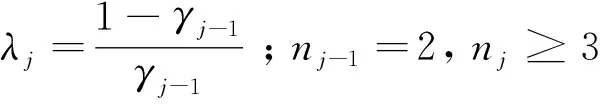
2.3 G1连续组合曲线的构造
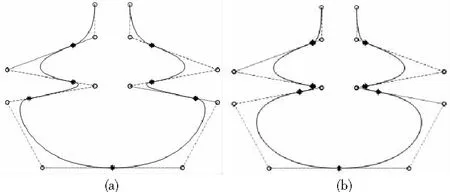



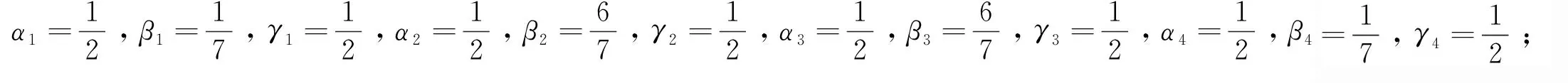
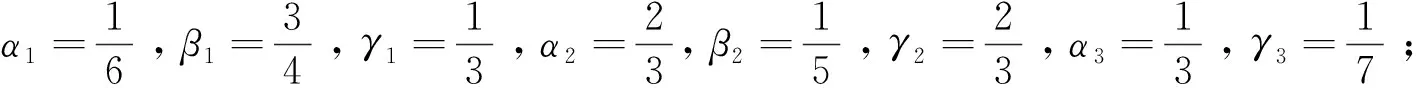
2.4 曲线的G2拼接条件
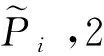
3 曲面及其应用
3.1 曲面定义及G1连续拼接条件
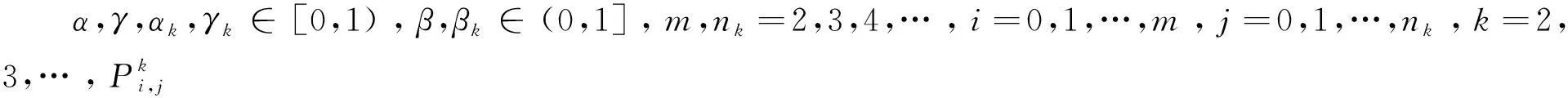

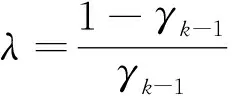
3.2 G1连续组合曲面的构造
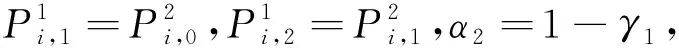

4 结束语

