面向深海着陆器全局动态路径规划方法

吕超,李思念, 刘爽*,,潘彬彬

(1.上海海洋大学 工程学院,上海 201306; 2.上海海洋大学 海洋科学学院,上海 201306)

21世纪是“海洋世纪”,海洋中蕴藏着丰富的生物资源、矿产资源等,是具有极大发展潜力的战略空间。深海着陆器作为一种用于海洋探测的自主载体系统,它们通常部署在几百到6 000 m深的海底,以自由落体方式到达海底,超出了遥感和常规定位系统的探测范围[1]。与自主水下航行器相比,着陆器具有结构简单、使用方便、成本低及探测时间长等优势,在深渊领域具有广阔应用前景[2]。2006年,英日合作的“HADEEP”项目,通过深海着陆器完成深海图像采集工作,并首次捕捉到深渊生物[3]。2016年,我国成功研制全海深着陆器,并通过所携带作业工具、摄像机和传感器等,成功捕获深海生物,采集到深海沉积物、水样,并拍摄下珍贵的影像资料等[4]。目前,着陆器多为无动力潜水器,部署在海底之后,进行定点探测、原位实验,无法改变其位置。本文提及的移动式深海着陆器搭载动力系统,可小范围移动,以实现多点探测,因此需要具备可靠的自主导航能力。

路径规划技术是实现移动式深海着陆器自主导航的关键技术之一。在障碍地形已知的情况下,以路程最优,安全性最好,等深度航行等为指标,规划一条最优路径,同时实现动态避障。针对路径规划问题,已经开展了大量研究,传统方法包括A*算法、人工势场法、D*算法等,智能方法分为基于群体智能的算法和基于机器学习的路径规划算法等。张丹红等提出了一种融合A*算法和蚁群算法的最短巡逻路径优化方法,有效地缩短了路径长度,提高了路径平滑度[5]。张岳星等提出一种基于海图和改进粒子群算法的自主水下机器人全局路径规划的方法,规划出短航程、安全性高的全局路径[6]。王珂等提出了一种深度强化学习机器人路径规划方法,对未知环境有较好的探索能力[7]。蚁群算法作为群体智能算法,被广泛应用于路径规划问题,但其存在一些问题,例如收敛速度慢,随着空间维度的增加,又面临算法计算量和复杂度较大的问题。刘贵杰等提出了一种改进蚁群算法,以降低机器人的能耗为目标,提高了续航能力,但没有考虑动态避障能力[8]。刘利强等提出了一种优化路径搜索的改进蚁群算法,能够有效地实现三维空间的路径规划,但是算法计算速度有待提高[9]。李宪强等提出了一种新的寻优方法,通过引入势场引导函数改进蚁群算法,能够有效的实现三维路径规划,但不具备动态避障能力[10]。为此,本文提出了一种融合算法,基于传统蚁群算法,构造了顾及全局路径规划且能提升算法收敛速度的评价函数,并通过简化栅格地图以实现降低算法的复杂度,同时设计了一种路径点选取策略,剔除危险点和非必要的转折点,并将选取后的路径点应用于人工势场法进行实时路径规划,实现等深度航行,使路径更加平滑,同时利用环境探测传感器反馈的动态障碍物信息,实现实时避障。

1 三维空间建模

三维空间建模是对深海着陆器运行空间的环境信息进行描述,是路径规划的重要内容,对路径规划方法的选取具有决定性作用。在移动式深海着陆器三维路径规划问题中,主要针对较小的全局搜索空间,本文采用规则格网模型建立海底三维地形图。路径规划空间被视为一个立方体空间ABCD-A′B′C′D′,空间大小为200 m×200 m×20 m。如图所示,建立直角坐标系,平面ABCD位于xoy平面,根据栅格地图的特性,将ABCD平面划分成100×100的网格,网格分辨率为2 m,如图1所示。

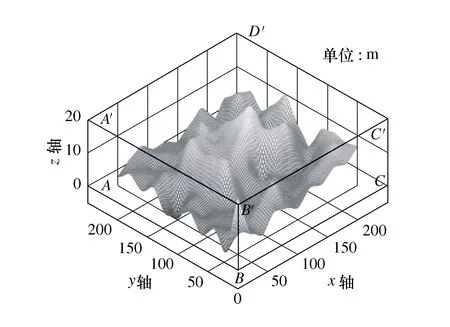
图1 三维地形图

2 改进蚁群算法

2.1 信息素表示

在模拟深海着陆器的工作环境时,对三维空间进行建模,将空间离散化,用各点坐标表示三维空间的位置,这些坐标点即为蚂蚁的搜索节点,信息素值存储在各坐标点中,信息素的值越大,蚂蚁选择该点的概率越大。信息素更新分为全局更新和局部更新。全局更新是指程序迭代一次,即种群中所有蚂蚁都从起点到达终点,对全局路径的信息素值进行更新,其更新值取决于路径长度,选择其中最短的一条路径,更新该条路径各个坐标点的信息素值,更新策略表达式为

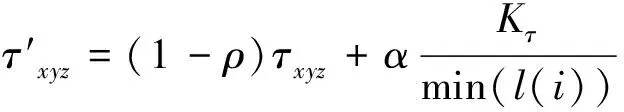
(1)

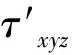
局部更新是由于蚁群算法具有随机性,易陷入局部最优解,故引入信息素的衰减系数,当蚂蚁经过一点后,对该节点信息素值的更新,减少蚂蚁陷入最优解的概率,信息素局部更新的策略表达式为

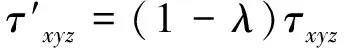
(2)

式中λ为局部更新信息素的衰减系数。

2.2 启发函数设计

启发函数是影响蚁群算法性能的重要因素。在移动式深海着陆器三维路径规划问题中,启发函数的设计需要考虑安全性、路径长度[11]、路径偏移程度。根据以上要求设计了启发函数H(x,y,z),即

H(x,y,z)=Sω1×Dω2×Mω3

(3)

式中:S为安全启发影响因子;D为距离启发影响因子;M为路径偏移容忍度;ω1、ω2、ω3为各影响因子的重要性系数。

1)安全启发影响因子

为保证深海着陆器的航行安全,使机器人避开障碍地形,引入安全启发影响因子S,S表示深海着陆器在可搜索范围内的下一点是否可以到达,S(x,y,z)的判定依据表达式为

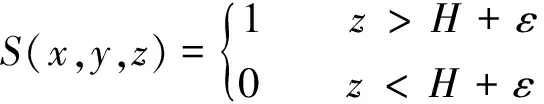
(4)

式中:H为地图高度;ε为深海着陆器到障碍地形的最小安全距离。

2)距离启发影响因子

为使路径规划距离尽可能短,在可搜索空间内,尽可能选取路径最短的点,同时考虑下一节点到终点的距离,引入距离启发影响因子D,D(x,y,z)的计算式分别为:

D=D1(xb,yb,zb)+D2(xb,yb,zb)

(5)

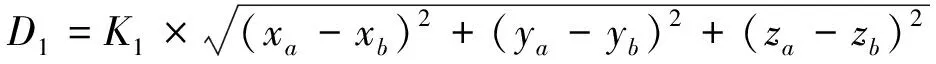
(6)

(7)

式中:(xa,ya,za)为深海着陆器当前所在的坐标点;(xb,yb,zb)为可搜索范围内的坐标点;(xc,yc,zc)为终点坐标;K1、K2为常系数。

3)路径偏移容忍度

理想情况下,深海着陆器在路径规划过程中,在保证路径较短的情况下,能够绕过障碍地形,避免频繁的上浮和下潜,使路径尽可能的保持在同一水平面,实现等深度绕行,这将有助于减少机器人的能耗,同时提升算法的收敛速度。因此,设计了路径偏移容忍度影响因子M,其中包含横向偏移容忍度和纵向偏移容忍度,表达式为

M=M1+M2

(8)

式中:M1为横向偏移容忍度;M2为纵向偏移容忍度。

横向偏移容忍度M1计算公式为

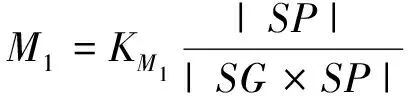
(9)

式中:KM1为横向路径偏移容忍度重要性系数;S、G、P分别为起始点、终点、下一可行点在XOY平面的投影。

纵向偏移容忍度M2计算公式为

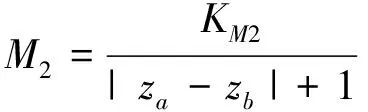
(10)

式中KM2为纵向路径偏移容忍度重要性系数。

横向偏移点线距离如图2所示。

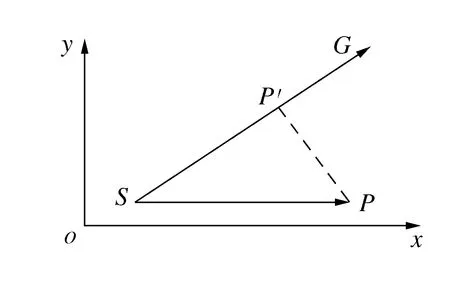
图2 横向偏移点线距离示意图

2.3 蚁群搜索策略

为了降低算法复杂度,提高算法的收敛速度,首先简化栅格地图,然后给出深海着陆器运行的搜索策略。取x轴方向作为路径规划的主方向,y轴方向为横向运动,z轴方向为纵向运动。设定允许机器人横向运动和纵向运动的最大移动距离,当蚂蚁沿着主方向前进,在位于点(x,y,z)时,对下一个点的搜索就形成一个简化的可搜索空间,根据启发函数来计算可搜索空间内各点的选择概率。简化的可搜索空间如图3所示。

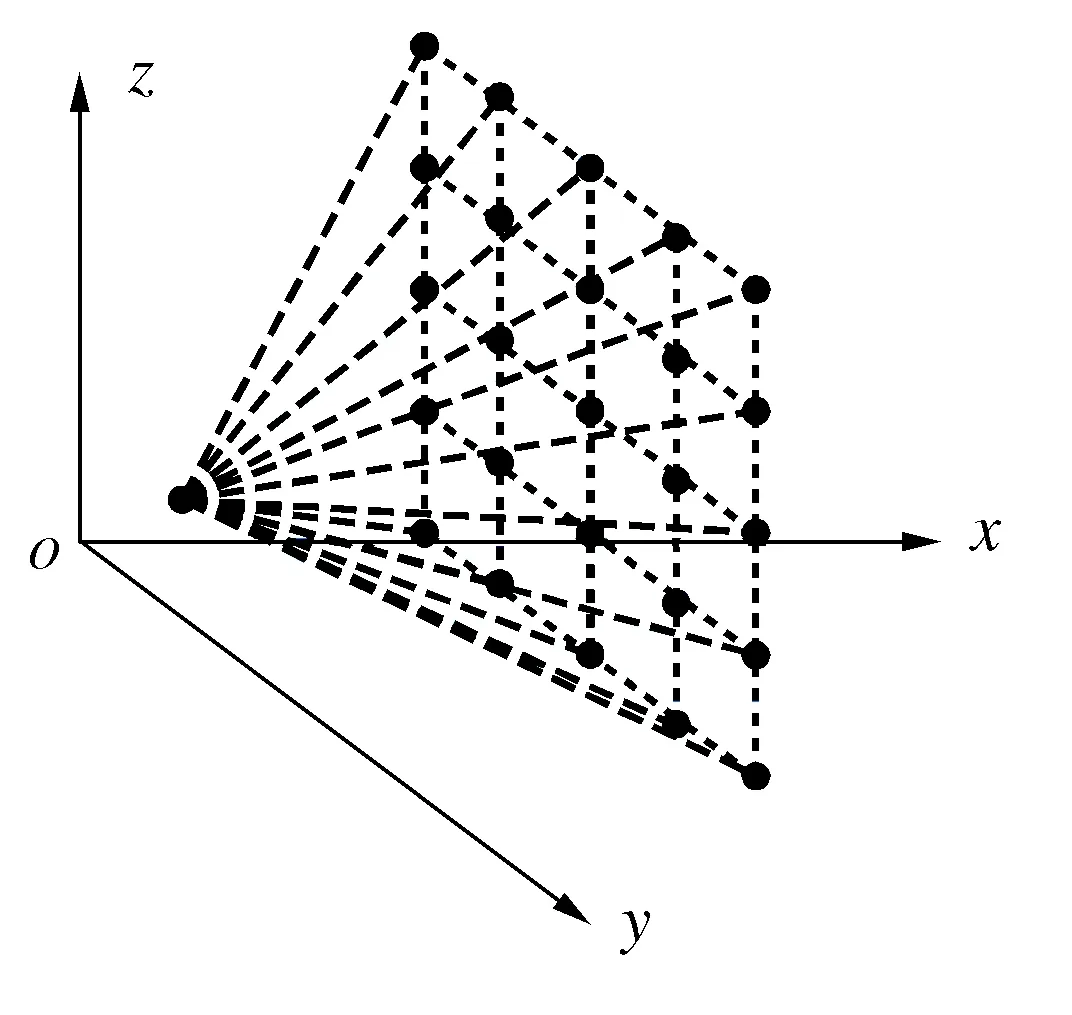
图3 蚂蚁可搜索空间

3 人工势场法

人工势场法将机器人在空间中的运动,抽象成在势场中的运动,势场由引力场和斥力场组成,终点对机器人产生引力,障碍物对机器人产生斥力,通过求两者合力来规划机器人的运动,势场场函数[12-13]表达式为

U(s)=Uatt(s)+Urep(s)

(11)

式中:s为深海着陆器的坐标点;Uatt为引力场;Urep为斥力场;U(s)为s点的势场和。

势场是引力和斥力同时作用下的结果,其中引力和斥力的大小分别为引力场、斥力场的负梯度,深海着陆器在势场中的受力表达式为:

(12)

式中:F(s)为深海着陆器所受合力;Fatt(s)为深海着陆器所受引力,引导着陆器到达目标点;Frep(s)为深海着陆器所受斥力,使着陆器远离障碍地形。

传统人工势场法中,引力与当前点和目标点的距离呈正相关,当距离较远,引力将偏大,在斥力较小的情况下,可能会使着陆器与障碍地形的距离小于安全距离,故引入引力场修正函数,引力场大小计算公式为:

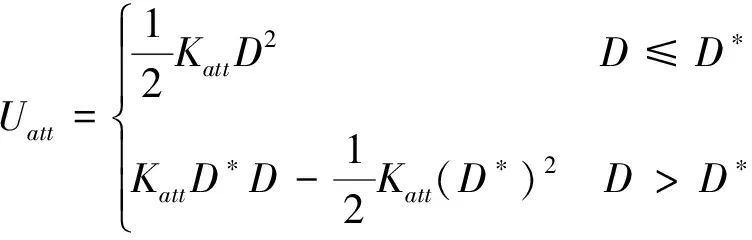
(13)

式中:Katt为引力系数;D*为距离阈值;D为深海着陆器与目标点的距离。

根据引力场函数,计算引力大小,引力方向指向目标点,引力函数为:

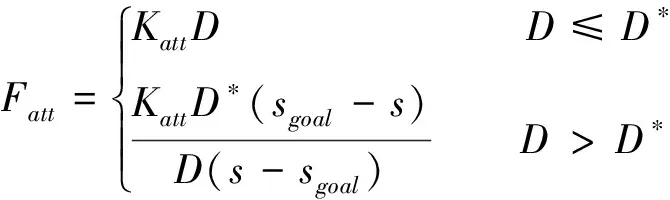
(14)

式中sgoal为目标点坐标。

传统人工势场法存在目标点附近有障碍时目标不可达的问题[14-15],故引入距离影响函数,斥力场大小计算公式为:

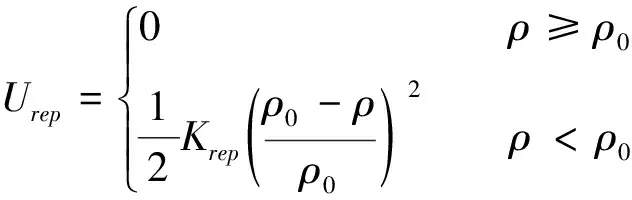
(15)

式中:Krep为斥力系数;ρ0为障碍物距离阈值;ρ为障碍物距离,即当深海着陆器与障碍物的距离大于ρ0,则该障碍产生的斥力场为0,可以有效的消除较远障碍物对深海着陆器路径规划的影响,其值受深海着陆器的航行速度、加速度影响。

当深海着陆器与障碍地形的距离小于等于ρ0,斥力的计算公式为

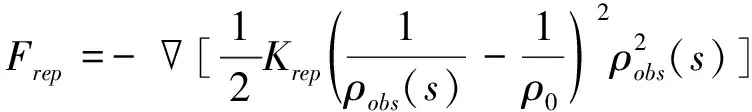
(16)

根据以上公式,可以计算斥力大小,斥力方向为障碍点与深海着陆器连线方向,每个障碍点产生的斥力可以分解为x轴、y轴、z轴3个方向的力,即:

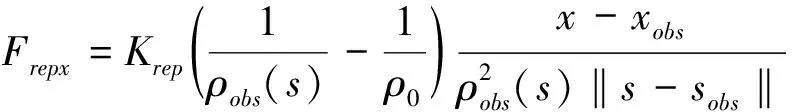
(17)

(18)

(19)

综上,当深海着陆器处在多障碍地形的复杂环境中,其势场和受力公式分别为:

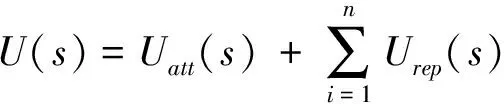
(20)

(21)

式中:n为当前深海着陆器与障碍地形的距离小于ρ0障碍点个数,障碍点产生的斥力Frep=Frepx+Frepy+Frepz,深海着陆器所受合力为引力和斥力的矢量和。

在势场中的受力方向如图4所示。

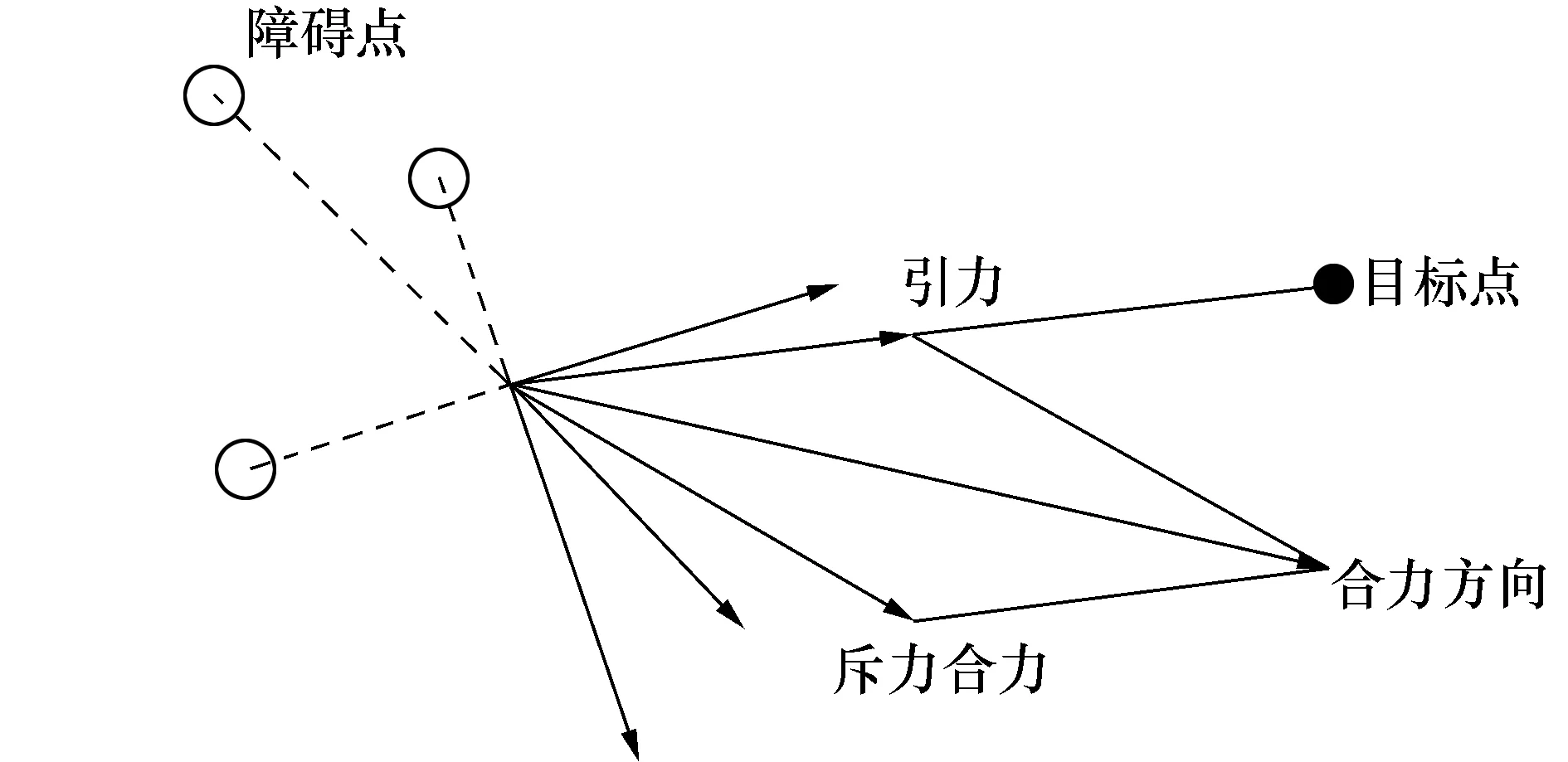
图4 深海着陆器在势场中的受力方向

4 融合算法

人工势场法根据检测到的实时环境信息,实现实时路径规划,具有良好的避障能力,但是该算法不能满足全局路径规划的最优要求,同时存在陷入局部最优的问题。因此,首先采用改进蚁群算法进行全局路径规划,选取全局路径规划的关键点,再融合人工势场法进行局部避障,以实现全局动态路径规划。关键点选取规则如下:

1)剔除危险点;

2)提取关键转折点,剔除冗余转折点,使两相邻路径点之间没有障碍物,且新路径与障碍物距离大于最小安全距离。

具体策略如下:设剔除危险点后的路径点集合为{Lk|k=1,2,…,n},连接L1L3,若L1L3连线不经过障碍物,且与障碍物的最小距离大于ρ0,则继续连接L1L4,直至L1Lk的连线与障碍物的最小距离小于ρ0,则连接L1Lk-1并删除冗余转折点;从点Lk-1开始,重复以上操作,直至路径搜索完毕。关键点选取平面示意图如图5所示。

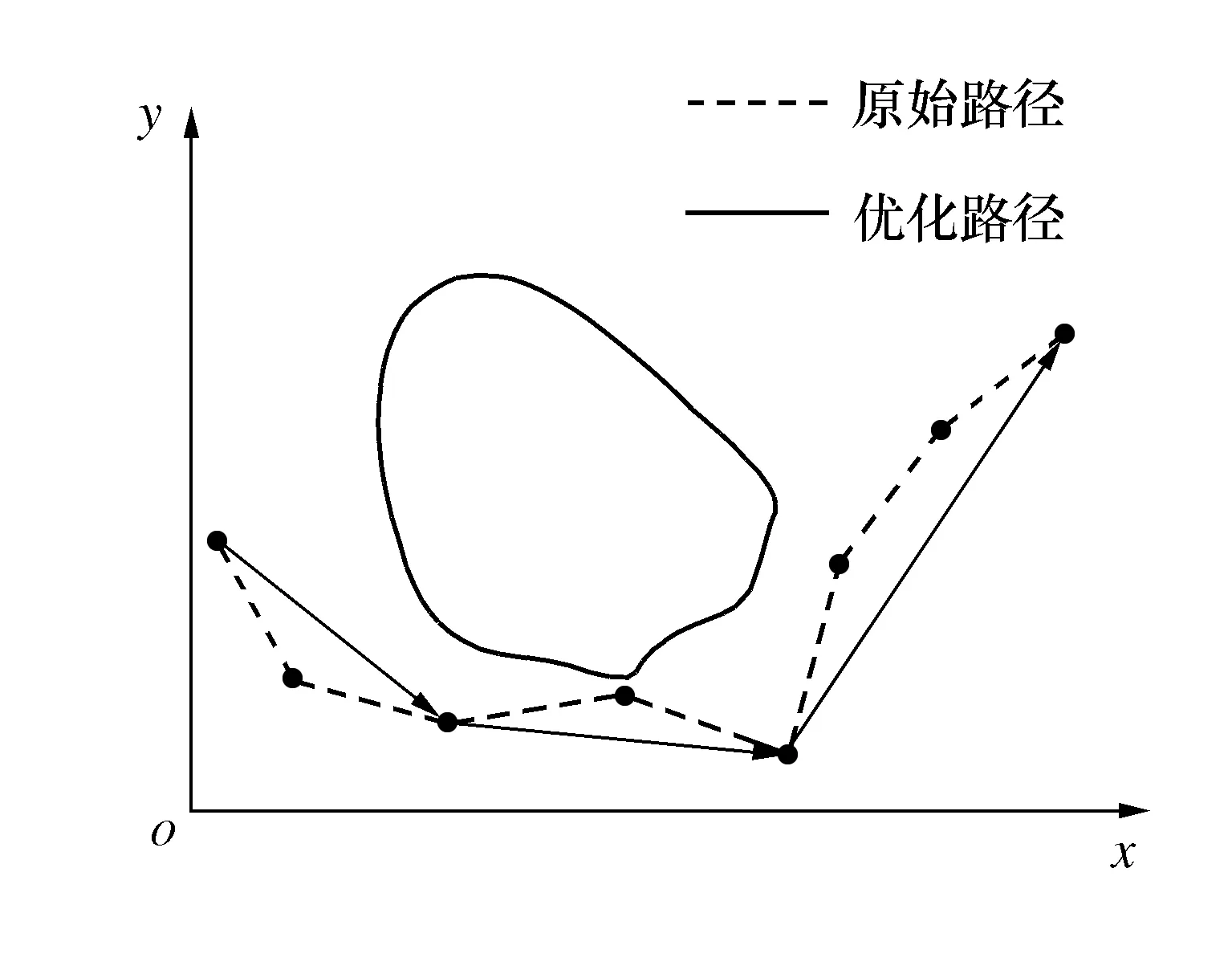
图5 路径点选取平面示意图

为了避免人工势场法陷入局部最优,将以上关键点视为人工势场法路径规划的子目标点,设计了一种顾及全局的势场函数,表达式为

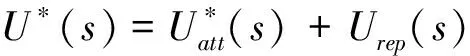
(22)

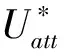
融合算法流程如图6所示。

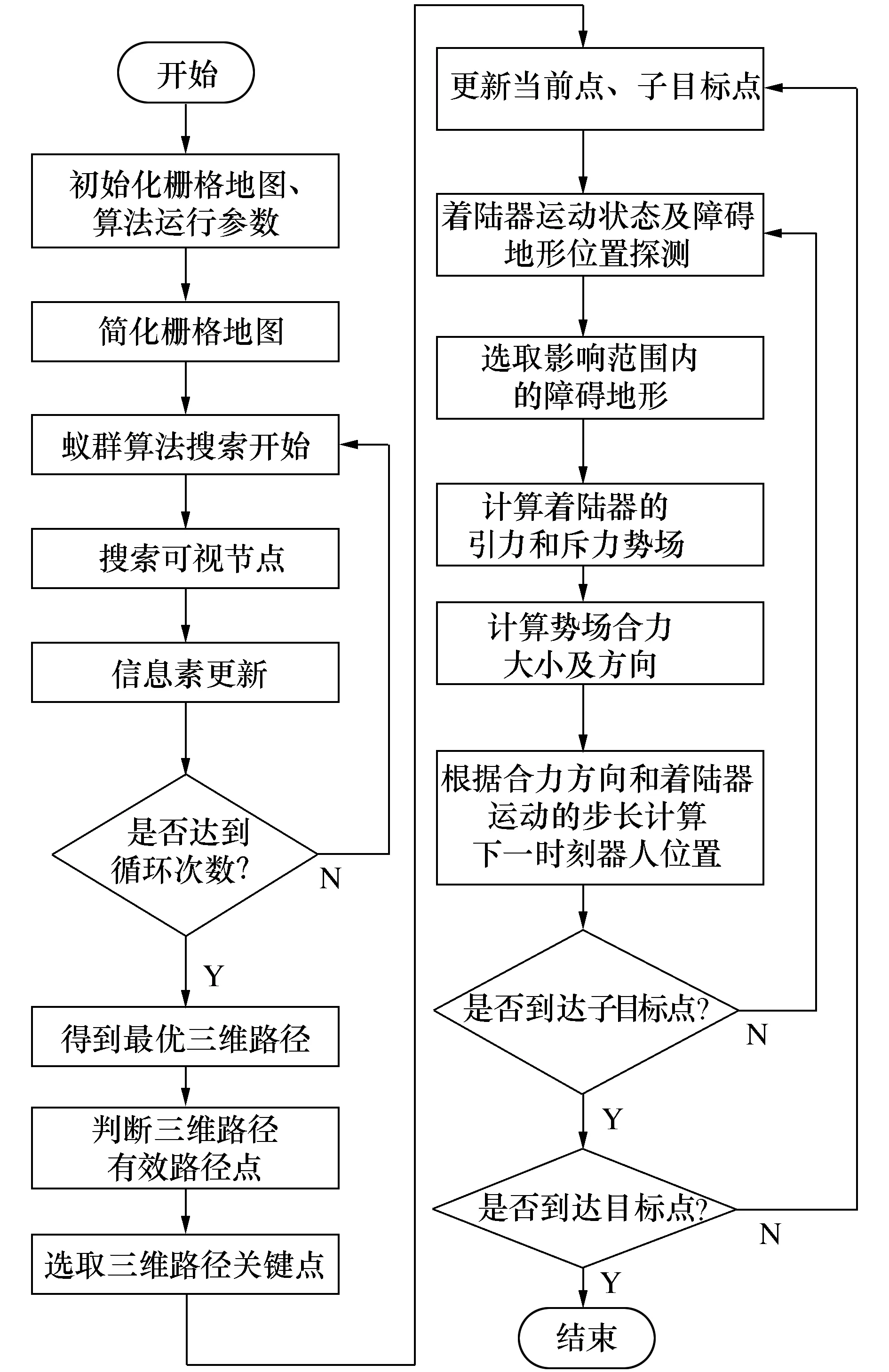
图6 融合算法流程图

5 实验算例

为验证算法的有效性,使用MATLAB R2018a软件编程,建立虚拟地图环境,模拟移动式深海着陆器从当前点到下一理想探测点的路径规划。仿真实验基于三维栅格地图场景,场景大小200 m×200 m,地形最高点20 m,起始点坐标为(0,75,70),终点坐标(100,45,60)。

5.1 实验算例1

实验I首先采用传统蚁群算法的启发式信息进行全局路径规划,为有效提高蚁群算法的收敛速度,缩短运算时间,实验场景设置为简化后的栅格地图,网格分辨率为10 m,如图7所示。程序各主要参数设置见表1。实验结果如图8所示。

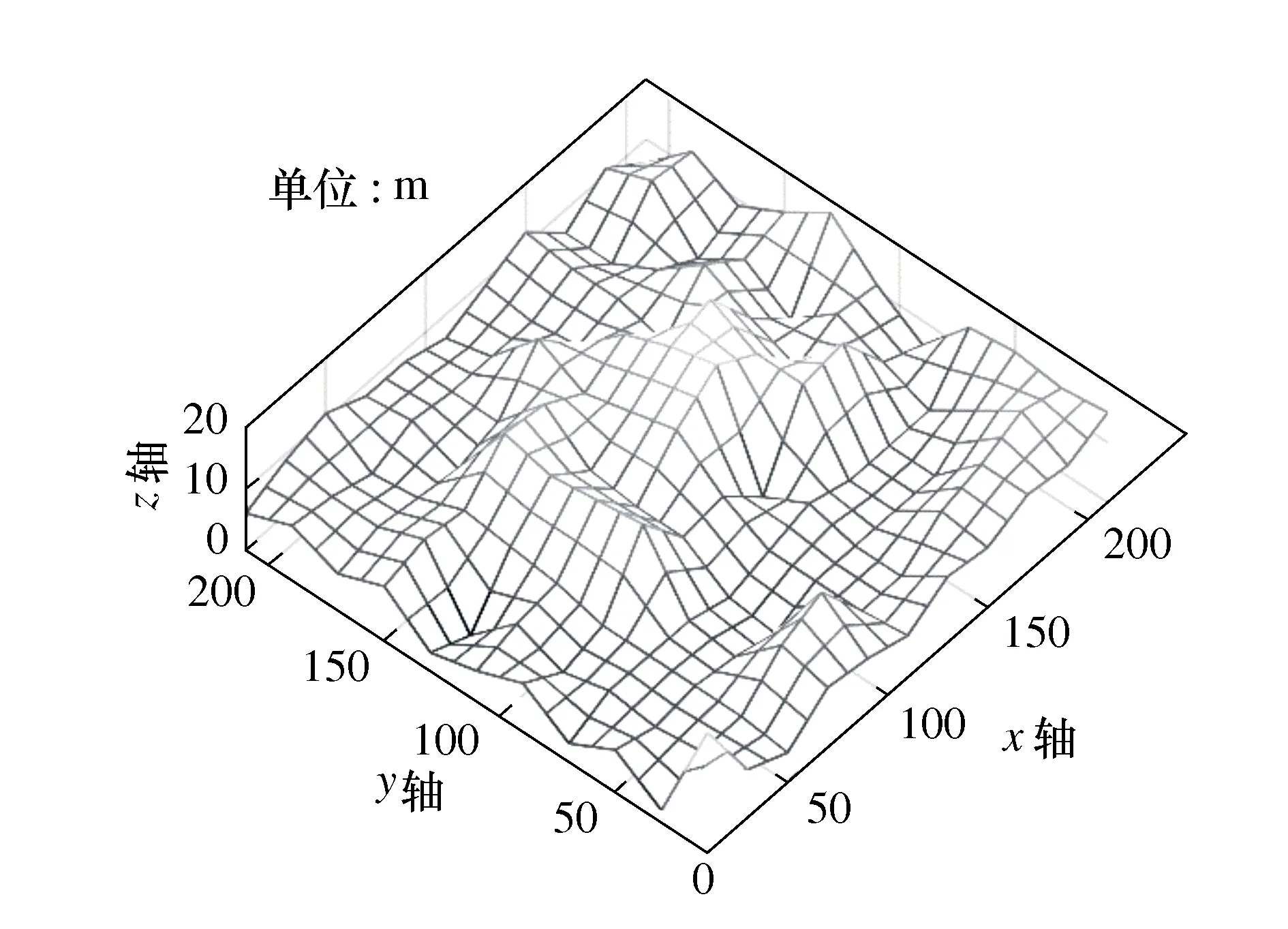
图7 简化后的三维栅格地图

表1 主要参数设置

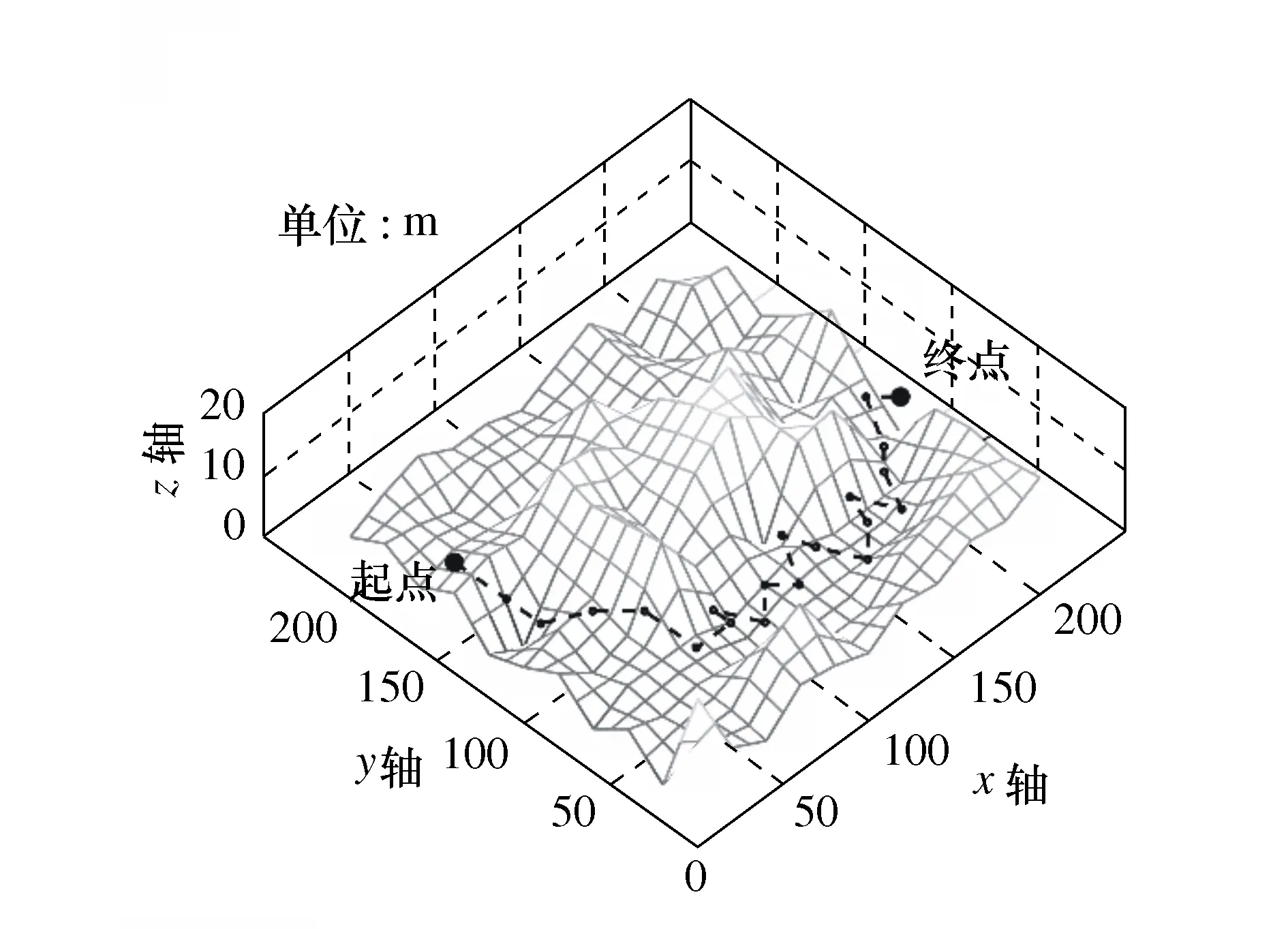
图8 蚁群算法三维路径规划

由图8可以看出,传统蚁群算法能够规划出一条完整的全局路径,且能很好避开障碍地形,但是规划出的路径有较大的震荡。

在相同仿真环境下及参数配置下,改进蚁群算法实验结果如图9所示。

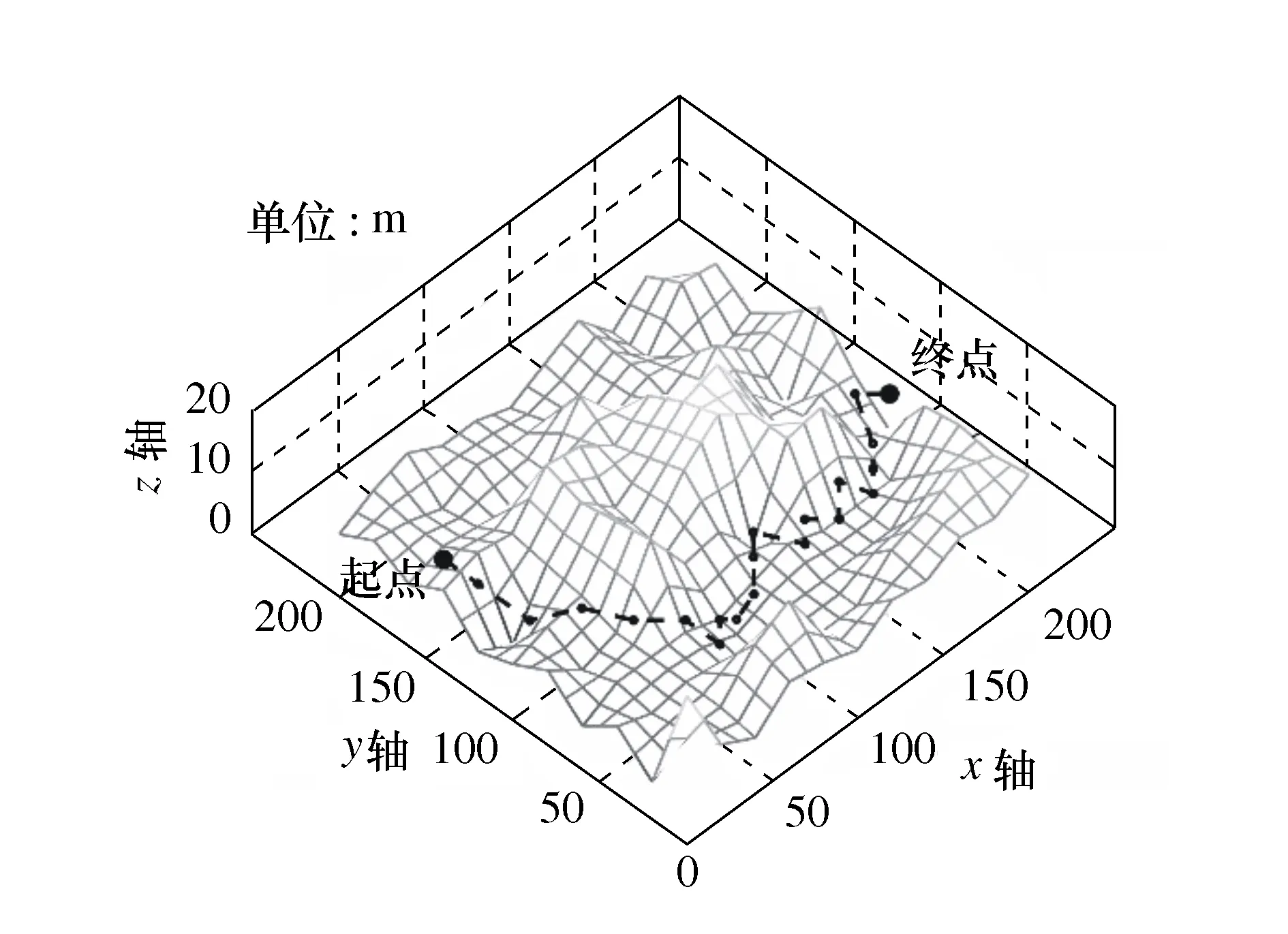
图9 改进蚁群算法三维路径规划

由图9可见,引入了新的启发函数的改进蚁群算法,能够明显改善路径,路径震荡减少,在个别点出有出现抖动,且能够很好的实现避障功能;但是改进蚁群算法和传统蚁群算法都不具备实时避障的能力。

从图10可以看出,改进蚁群算法在相同迭代次数下,最佳个体的路径长度始终小于传统蚁群算法,传统蚁群算法迭代200次的最佳路径长度为365 m,改进蚁群算法迭代200次的最佳路径长度为337 m,说明改进蚁群算法的收敛速度有所提升。

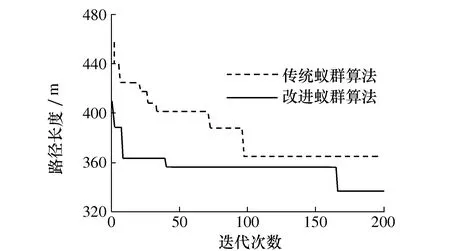
图10 改进前后蚁群算法最佳个体路径长度变化

为进一步验证改进算法与传统算法在路径长度和平稳性方面的差异,同时考虑到蚁群算法的路径搜索具有随机性,对每种算法进行100次独立运算,规划出100条路径。实验结果如图11所示。并对所有路径的垂向偏移距离求和,分析两种算法规划的路径的垂向偏移程度,结果如图12所示。

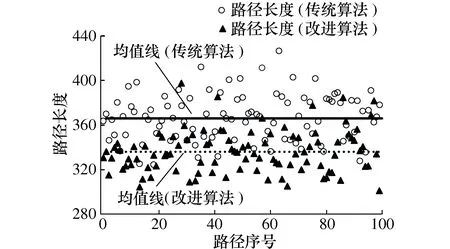
图11 路径长度对比

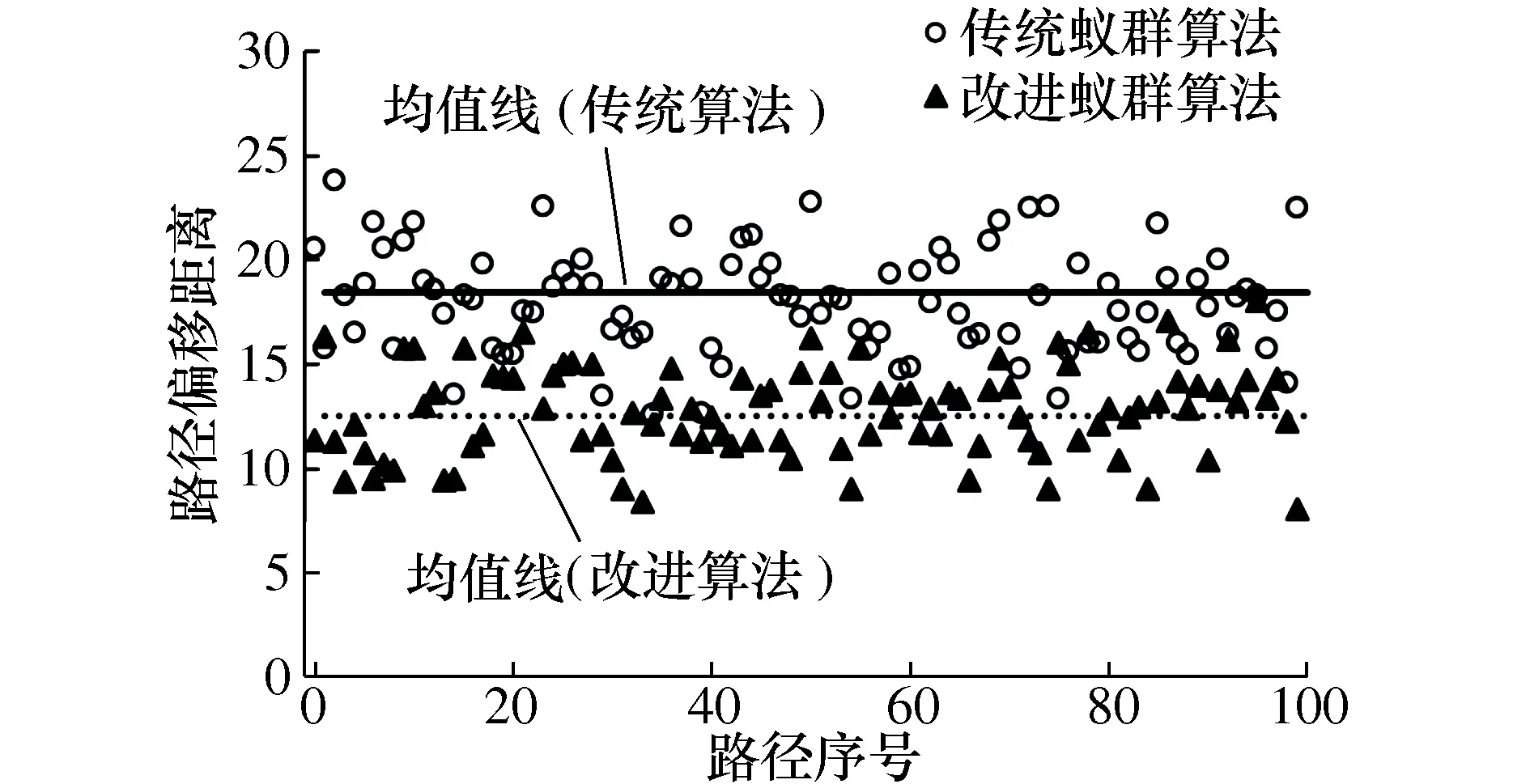
图12 路径垂向偏移程度对比

由图11传统蚁群算法和改进蚁群算法多次独立运算后的结果可以看出,传统算法100条路径长度均值为366 m,改进算法路径长度均值为336 m,在算法迭代次数相同的情况下,改进算法在路径长度上明显小于传统算法。

由图12可以看出,传统蚁群算法和改进蚁群算法规划的路径,其垂向偏移距离均值分别为18.46 m和12.5 m,改进算法在路径平稳性上明显优于传统算法。

5.2 实验算例2

实验2主要考察融合算法的全局路径规划和动态路径规划能力,同时对比传统人工势场法规划的路径。实验场景为网格分辨率2 m的栅格地图。采用传统人工势场算法进行路径规划,路径规划结果如图13所示。

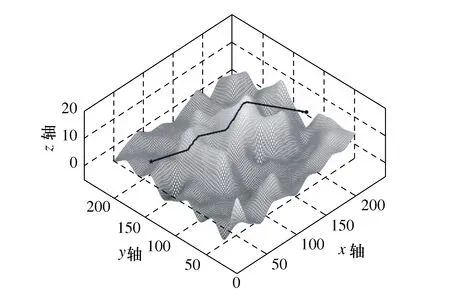
图13 传统人工势场算法三维路径规划

采用本文提出的融合算法,在实验1的基础上,选取改进蚁群算法产生的全局路径中的有效关键点作为连续的子目标点,以验证本文融合算法的全局路径规划性能,如图14所示。

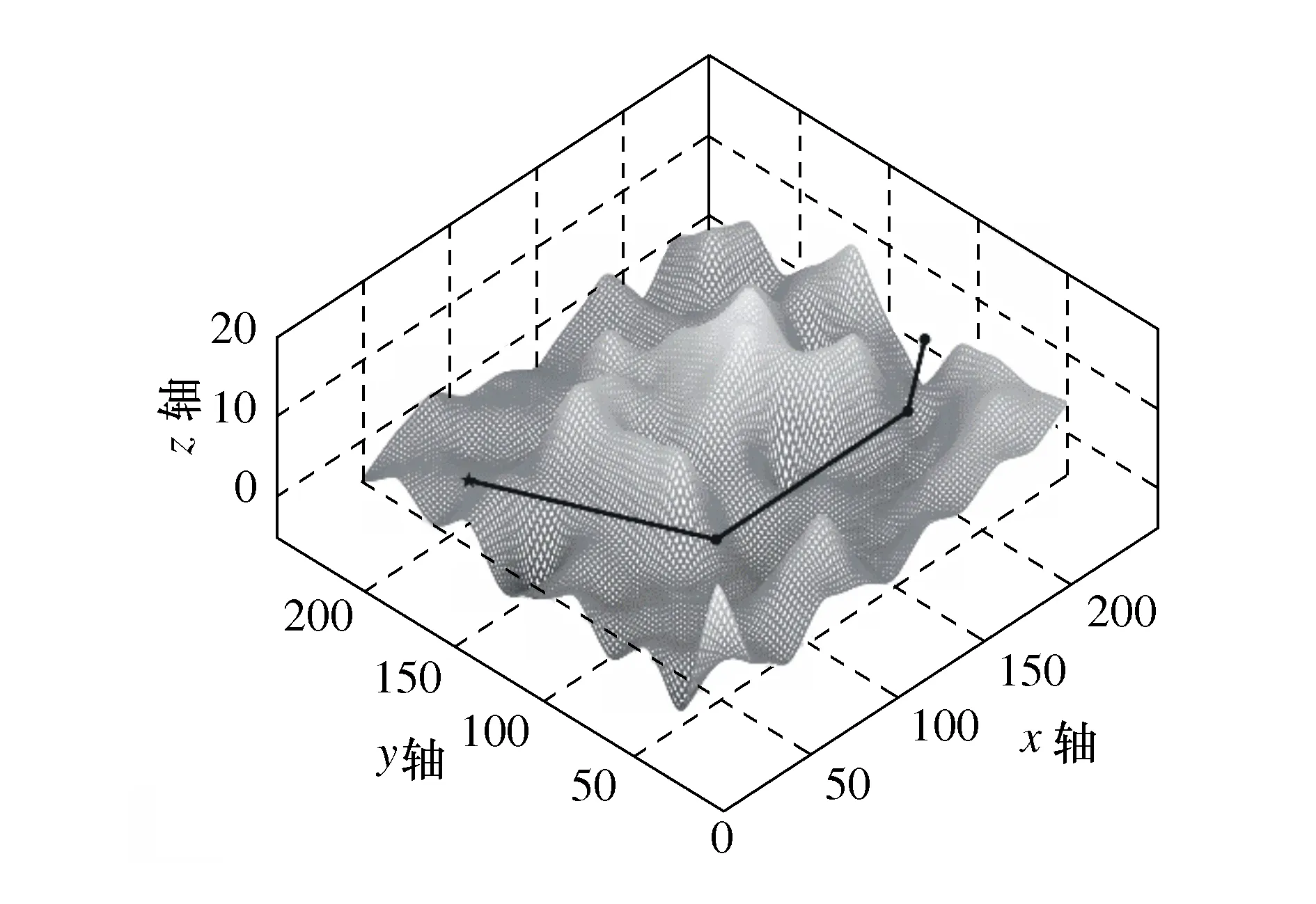
图14 融合算法全局路径规划

为进一步对比传统人工势场法和本文算法的路径平稳性,将两种算法规划的路径向xoz平面投影,如图15所示。同时增加动态障碍物,以验证本文融合算法的全局动态路径规划性能,如图16所示。

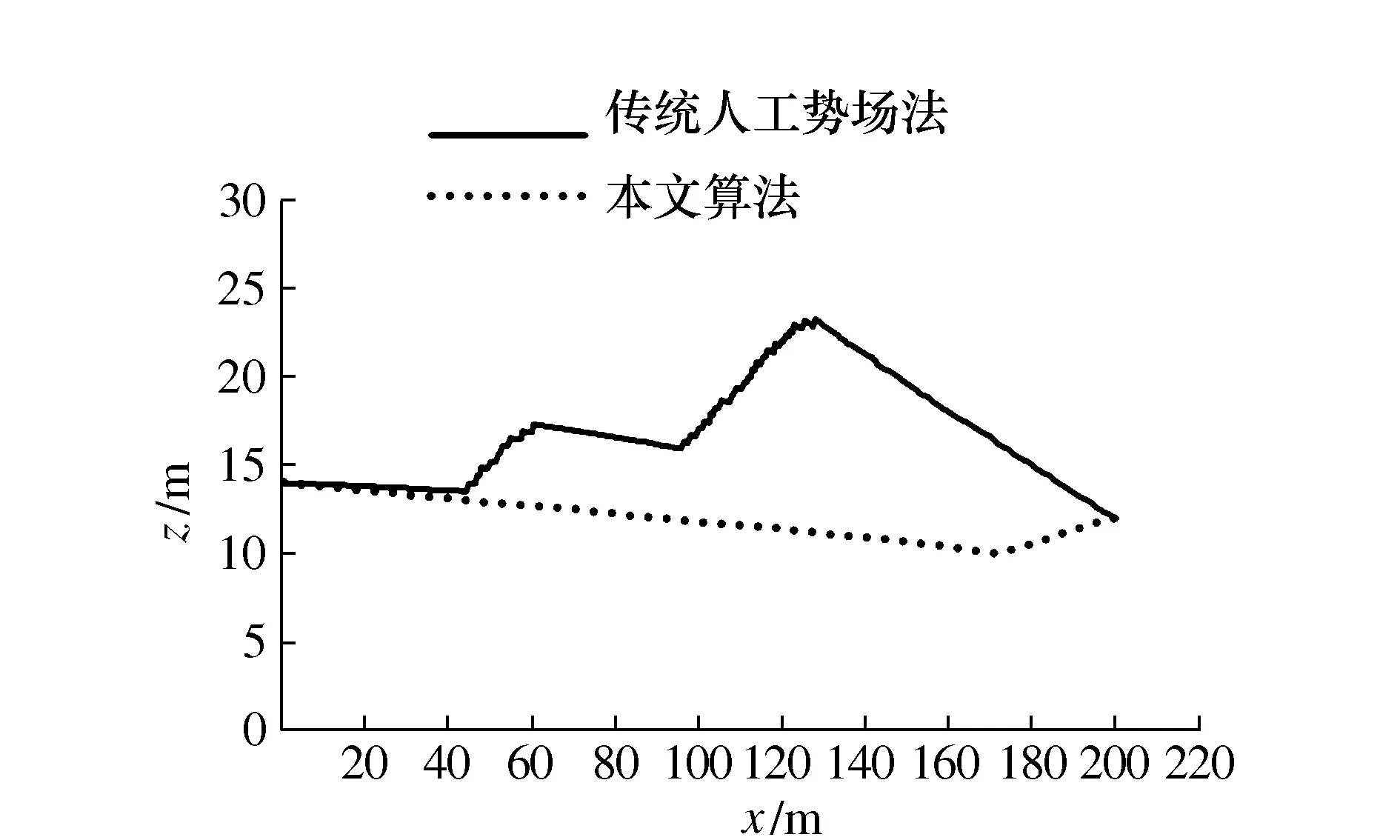
图15 路径在xoy平面投影

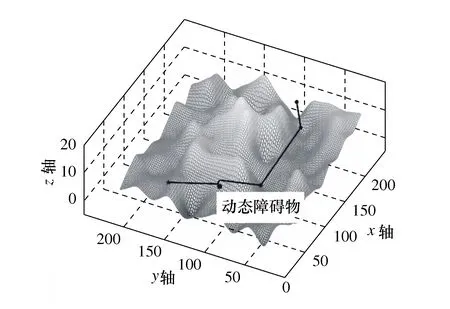
图16 融合算法全局动态路径规划

由图13和图15可知,传统人工势场算法在地形不复杂的情况下能够完成路径规划,但不能实现等深度航行,路径方向始终指向终点方向,即引力方向,遇地形障碍时,规划的路径有较大的起伏,总路径长度为220 m,垂向偏移距离28 m。

由图14和图15可知,引入关键点作为子目标点的人工势场算法能够明显的改良原有路径,所产生的路径继承了改进蚁群算法全局路径规划的优良性,路径长度259 m,增加17%,垂向偏移距离6 m,减少78%。与传统人工势场法路径相比,虽然路径长度变长,但是路径更加平稳,起伏波动较小。

由图16可知,当环境信息中引入动态障碍物后,本文融合算法可绕过动态障碍物,能实现实时避障,且路径能够保持全局最优性,基本实现等深度航行,达到预期目标。

6 结论

针对移动式深海着陆器全局动态路径规划问题,本文提出了一种融合改进蚁群算法和人工势场法的三维全局动态路径规划方法：

1)基于传统蚁群算法,设计了基于路径偏移的启发函数,同时提出简化栅格地图和优化搜索空间的方法,提升了蚁群算法在三维路径规划中的收敛响应速度。

2)基于传统人工势场法,设计了引力场修正函数和斥力场距离影响函数,保证了目标点较远时,人工势场法规划的路径不会碰撞障碍地形,同时解决了近目标点有障碍物时,目标点不可达问题。

3)提出了融合改进蚁群算法和人工势场法的规划方法,构造了顾及全局路径规划的势场函数,保证了三维动态路径规划的全局最优性。

实验算例结果表明,本文提出的算法在保证全局路径规划较优的基础上,提高路径的平滑性,实现等深度航行,同时具备良好的局部避障的能力。与传统蚁群算法相比,改进之后的蚁群算法收敛速度更快,路径更加平滑;与传统人工势场法相比,所提算法能够继承蚁群算法全局路径规划的优良性。由于蚁群算法是一种随机搜索的算法,不能够保证航线的最优性,同时在三维路径规划中蚁群算法运算时间较长,在提高蚁群算法的运算速度上仍有待进一步的探讨;在实现动态避障时,靠近动态障碍物的路径存在曲率变化不连续的问题,是下一步改进研究方向。