矩形通风管道清洁机器人机构设计与优化

银 枫，汪永明，李 祥

(安徽工业大学a.机械工程学院；b.特种重载机器人安徽省重点实验室,安徽马鞍山 243032)

通风管道用于工业和民用建筑的空气流通和降低有害气体浓度，是国家的基础设施之一。由于通风管道本身具有相对密封的环境，导致其内部积聚大量可吸入的固体颗粒，这些固体颗粒随着空气的流动进入室内，严重影响人们的身体健康[1]。通风管道尺寸通常较窄小，人工清理不便，且不能深入清理。随着机器人技术的快速发展，管道机器人由于体积小、质量轻的特性使得通风管道的深度清理得以实现[2]。

目前，国内外学者对管道机器人进行了系列研究并取得一定研究成果[3]。Panwar等[4]设计了一款智能清洁机器人，提高了机器人的避障能力与工作效率；Zhang等[5]设计了管道清洗机器人的自适应机构，通过调整履带脚之间的距离与角度，增加履带与管壁之间的接触面积，使机器人可用于直径在110～250 mm 之间的管道；谷忠朋等[6]开发了一种矩形管道清洁机器人，通过改变机器人支臂与水平面之间夹角来调节旋转刷的高度，使其在不同高度的管道中作业；田军委等[7]基于轮式移动机构设计了一种用于矩形通风管道的清洁机器人，由主刷头与辅助刷头进行清洁工作，辅助刷头为开合式结构，可在不同宽度的管道中作业；Sun 等[8]针对国内矩形通风管道的特点，提出了一种自适应调节机构，大幅度增强了机器人的适应能力；Hassan 等[9]建立了机械夹爪几何模型，基于遗传算法得到了夹爪抓取刚性物体表面的最佳力；Venkateswaran等[10-11]针对现有管道机器人单元尺寸过大、无法通过直角弯等问题，通过伸缩机构的静态稳定性分析确定相关设计参数，并通过MATLAB 计算出了机器人的最佳设计参数；于涛等[13]给出了机器人通过弯管的约束条件，并对清理机构连杆长度进行优化，工程应用与分析结果显示，由变径引起的误差降低了89%。目前，用于矩形通风管道的清洁机器人适应性差，只能用于单一高度的管道。鉴于此，设计一种变距矩形通风管道清洁机器人，通过改变自身高度而适应不同高度的管道，以期为管道机器人的物理样机制作奠定理论基础。

1 机器人结构设计

设计的机器人主要由驱动机构、变距机构与清灰机构三部分组成。通过SolidWorks 建立机器人三维模型，整体结构如图1，采用铝合金作为机器人机体与连杆材料，机器人整体质量为3 kg。

图1 矩形通风管道清洁机器人三维模型示意图Fig.1 Schematic diagram of 3D model of rectangular ventilation pipe cleaning robot

驱动机构由轮子、支架、连杆、齿轮组成，机器人前侧与后侧上部的轮子均为被动轮，后侧下部轮子由电机驱动，实现机器人的整体移动。驱动电机固定在支架上，两端支架通过连杆连接，转向电机通过齿轮传动带动支架转动，进而实现机器人的转向运动。

变距机构由平行四杆机构演变而来，由丝杠、滑块、顶杆、辅助杆、齿轮等组成。变距电机带动丝杠旋转，使滑块沿着丝杠轴向移动，顶杆推动后平行四杆机构转动，前平行四杆机构与后平行四杆机构通过齿轮传动使其同步运动，实现变距功能。顶杆中部设有弹簧，当变距机构局部受力产生突变时，可对其进行柔性补偿。

清灰机构由毛刷、波纹管、集尘箱、吸尘口等组成。毛刷布置于机器人顶部、底部与两侧，在电机的带动下扫落管壁灰尘，再通过机器人后端的吸尘口基于负压原理将灰尘收集至集尘箱内。

2 机器人受力分析

2.1 竖直管道中的受力分析

当机器人在竖直管道中作业时，为使机器人不下滑，机器人轮子与管壁之间的摩擦力应与自身重力相等[14]。变距机构的上侧与下侧对称，取其上侧为分析对象，如图2。机器人此时受到自身重力G/2，连杆对轮子的支撑力NA和NE，管壁对轮子的压力FA和FE，管壁与轮子间的摩擦力fA和fE。由图2可知，NAsinα与FA对点A的力矩为零，NEsinα与FE对点E的力矩为零，此时的静力学平衡方程为：

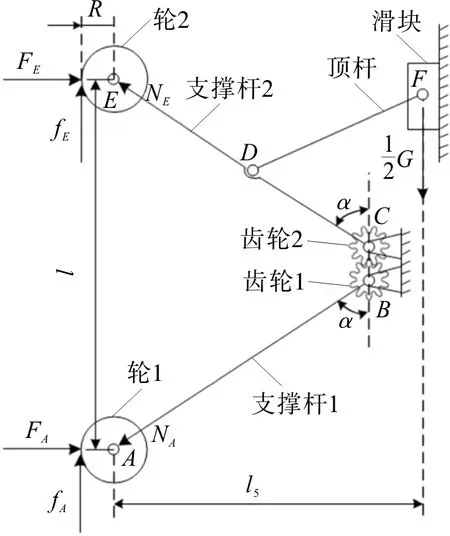
图2 机器人在竖直管道工作临界受力分析Fig.2 Critical force analysis of robot working in vertical pipeline

式中：α为支撑杆2 与齿轮中心连线间的夹角；μ为管壁与机器人轮子间摩擦系数；G为机器人自身重力；l为轮1到轮2的距离；R为轮子半径；l5为机器人质心延长线到轮子中心的距离。由式(1)可知

将G=30 N，l5=150 mm，μ= 0.5，R=25 mm代入式(2)可，求得NAsinα+NEsinα的最小值为180 N。

2.2 变距机构受力分析

变距机构的上侧与下侧对称，取其上侧为分析对象，如图3。滑块沿水平线方向左右移动，通过顶杆使支撑杆2 发生转动，支撑杆2 通过齿轮传动带动支撑杆1转动，从而达到变距的目的。

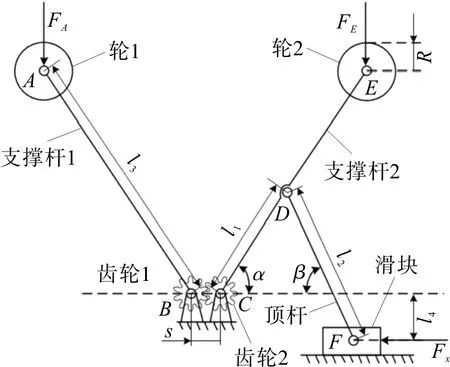
图3 机器人变距机构受力分析Fig.3 Force analysis of robot variable distance mechanism

机器人在竖直管道中运动时，轮胎与管壁之间的摩擦力应大于机器人重力：

式中：l1为支撑杆2 点C到点D之间的距离；l2为顶杆的长度；l3为支撑杆1 的长度；β为顶杆与水平线的夹角；l4为滑块中心到水平面之间的距离；s为齿轮1与齿轮2的中心距；x为机器人在水平方向的虚位移；y为机器人在竖直方向的虚位移。对式(4)进行微分可得到

根据虚功原理可知，主动力对虚位移所做功为零[14]，即

式中Fx为滑块所受水平推力。

由式(5)，(6)可得出管壁对轮胎的正压力与水平推力的关系

上侧变距机构与下侧变距机构对称，因此施加在滑块上的总推力F为

变距过程中电机带动丝杠旋转，从而使滑块移动。因此，可得出电机的驱动力矩T与滑块所受总推力F的关系为

式中：P为丝杠螺母的导程；η为丝杠螺母的传动效率。

3 机器人变距机构优化设计

3.1 设计变量

由上述分析可知，变距机构所需水平推力与支撑杆上点C到点D的距离l1、顶杆长度l2、支撑杆长度l3、支撑杆2与齿轮中心连线间的夹角α、顶杆与水平线的夹角β有关。对杆长进行优化，故取设计变量为

3.2 目标函数

在变距过程中，为追求更高的变距效率及降低能源消耗，应使电机的输出扭矩尽可能小，故将电机的最小驱动力矩作为优化目标。由式(9)可知，滑块所受总推力F与电机扭矩成正比，故将F的取值最小化且将其作为目标函数，则有

3.3 约束函数

考虑到机器人在管内运动，自身结构应尽量紧凑，需对各杆件长度进行约束；为避免变距机构在死点位置附近工作，应使支撑角α尽量增大，但随着α的增大，机器人高度方向尺寸迅速变大，无法满足在低高度管道中工作的需求，故需对支撑角α进行约束；变距机构应满足机器人在高度为200～300 mm 的管道中工作的需要。因此，建立约束条件如式(12)。

式中h为机器人的整体高度。

3.4 参数化建模与优化设计

建立模型时，首先确定关键变量，将模型的关键变量以设计变量代替，在模型的进一步分析时，只需更改相应设计变量的值便可改变模型[15-16]。机器人变距机构所用设计变量与常量如表1。采用参数化点坐标的方式进行参数化建模，通过连接相应的点坐标即可完成模型的建立，通过修改点坐标更改模型，关键点参数化坐标如表2。

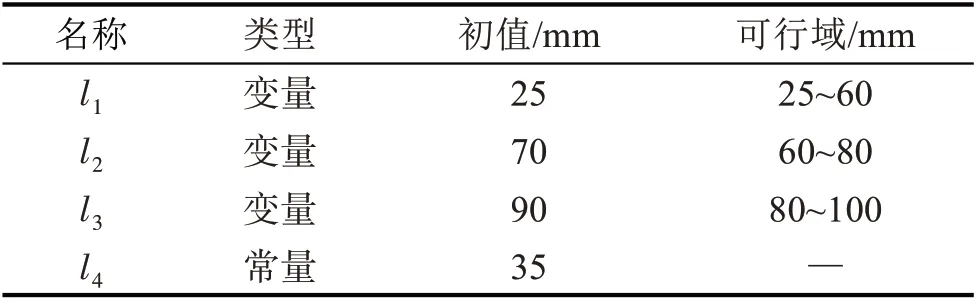
表1 设计变量与常量Tab.1 Design variables and constants

表2 关键点参数化坐标Tab.2 Parameterized coordinate of key point

完整的参数化模型除以上工作外，还需添加相应约束条件以限制各杆件之间的相对运动[17]。各部件间相应约束关系如表3。

表3 各部件间约束关系Tab.3 Constraint relationship among components

由式(2)可得点A与点E处管壁施加给轮子的最小法向力共为180 N，假设点A与点E所受力的大小相同，则点A与点E所受的力均为90 N。在ADAMS中通过关键点坐标建立参数化模型，在点A与点E处各施加90 N 的力，方向垂直向下，等效管壁施加在轮子上的压力如图4。以滑块与地面连接的移动副所受合力为测量对象，通过ADAMS 中的OPTDES-GRG 算法对变距机构进行优化分析，结果如表4。由表4可看出，优化后移动副所受合力大幅减小。

表4 参数优化前后结果对比Tab.4 Comparison of results before and afterparameter optimization

图4 变距机构参数化模型Fig.4 Parameterized model of variable distance mechanism

将优化结果代入式(13)，求得机器人可适应的管道高度为220～293 mm。以力为纵坐标，迭代次数为横坐标绘制移动副所受合力的变化曲线，如图5。由图5可看出，移动副所受合力最小为229.41 N。

图5 移动副所受合力变化Fig.5 Change of the resultant force on moving pair

4 结论

1) 设计一款用于矩形通风管道清洁的可变距机器人，用于高度在220～293 mm 之间的管道。对机器人在竖直管道中的临界状态进行静力学受力分析可知，支撑杆需对轮子施加最少180 N 的正压力，可确保机器人在竖直管道中运动时不滑落。

2) 以滑块与地面间移动副所受合力最小为目标函数对机器人变距机构进行优化，得到约束条件下的最优杆长，提高了机器人整体的变距性能。优化后移动副所受合力减少了45.2%，优化效果明显，为变距电机的选型提供了理论依据。