基于自抗扰控制的线材打捆机电液力控制系统
张 翔,叶小华,彭 耀,黄建中
(1.安徽工业大学机械工程学院,安徽马鞍山 243032;2.安徽燊泰智能设备有限公司,安徽马鞍山 243000;3.液压振动技术安徽省工程技术研究中心,安徽马鞍山 243002)
线材打捆机是高线生产线自动打包的关键设备,包括压紧、打捆、扭结和剪切等工位[1-2]。其中打捆机压盘对线材的压紧为最重要的一步,决定着打捆的质量,故对压紧力的控制提出了较高要求。但打捆机的阀控缸液压系统存在较大的内部参数变化和外部负载力扰动,使得现有PID 控制效果不佳。为抑制液压系统中的扰动,目前主要采用自适应控制算法、最优控制算法、H∞鲁棒控制算法[3-5]。这些控制算法对系统模型的精度要求高,设计的控制器结构复杂、整定参数多。自抗扰控制(active disturbance rejection control,ADRC)是一种基于对被控系统外部和内部干扰进行估计并主动补偿的控制方法,能有效抑制系统干扰,系统具有较强的自抗扰能力[6]。ADRC 对系统模型精度要求较低、控制器结构相对简单,故其在汽车主动转向控制[7]、永磁同步电机控制[8]、飞行器姿态控制[9]以及液压系统控制[10-11]等方面广泛应用,但少见在线材打捆机方面的应用。
目前,对于阀控缸液压系统的自抗扰控制研究[12-15]多采用机理推导建模方法,这种方法需进行复杂的线性化处理,所建模型无法体现系统各状态变量的联系;忽略了控制阀动态特性对控制器阶次的影响,设计的控制器结构复杂、需整定参数多。鉴于此,设计基于ADRC 的线材打捆机电液力控制系统,采用适合于复杂非线性系统建模的功率键合图法[16-18],建立线材打捆机电液系统模型,通过零点配置的方法降低系统的阶次,以简化设计的控制器结构和所需整定参数,最后通过软件仿真验证系统的控制性能和抗干扰能力。
1 线材打捆机电液系统模型的建立
线材打捆机电液系统主要由比例伺服阀和液压缸组成,通过输入比例伺服阀的电压来控制阀芯位移,进而控制液压缸的输出力。比例伺服阀的输入为电压、输出为阀芯位移,其动态特性是一个典型的二阶振荡环节,故文中主要对以阀芯位移为输入、以力为输出的液压缸进行数学建模。
1.1 液压缸的数学模型
零开口四边滑阀控制非对称液压缸系统的功率键合图如图1。图1中:系统的压力源和回油箱阻力用力元代替,分别用p1和p8表示;四边滑阀阀芯与阀套形成的4 个节流孔用阻性元代替,分别用R1,R2,R3,R4表示;液压缸无杆腔和有杆腔用容性元代替,分别用C1和C2表示;液压缸的内泄漏用阻性元代替,用R5表示;液压缸所受的惯性、黏性和弹性负载力分别用惯性元、阻性元、容性元代替,分别用I,R6,C3表示;A1,A2分别为液压缸无杆腔和有杆腔的面积。

图1 阀控缸的功率键合图Fig.1 Power bonding diagram of valve controlled cylinder
由图1知,与C1连接的0节点处各功率键压力相等,且流量代数和为零,即有

式中q15,q16,q17,q23分别表示键合图中通过通道15,16,17,23的流量。由图1可知q15,q17,q23为:

式中:p16,p20分别为液压缸无杆腔和有杆腔的压力;v为液压缸活塞速度。又因C1作用元上q16为自变量、p16为因变量,故有

由式(1)~(3)可得
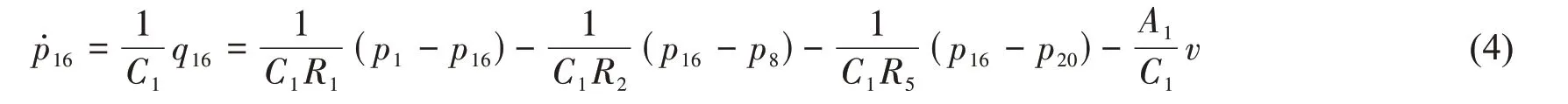
同理,对容性元C2连接的0节点作同样分析,可得

与代表各负载的作用元连接的1节点处各功率键速度相等、力代数和为零,即有

式中:F1和F2分别为无杆腔和有杆腔内油液对活塞的压力;F3,F4,F5分别为液压缸受到的黏性、弹性及惯性负载力。由图1可知F1,F2,F3,F4为:

式中:R6为黏性阻尼系数;x为液压缸活塞位移;C3为负载的柔度。又因在I作用元上F5为自变量、v为因变量,故有

联立式(6)~(8)可得
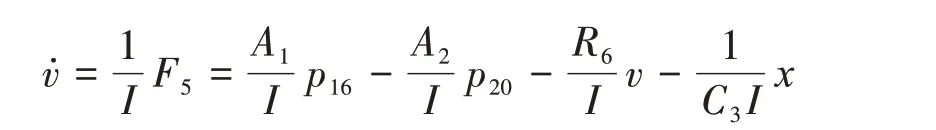
阀口通过流量q与阀芯位移x′和阀两端压差Δp的关系为

式中:kq为流量系数;w为面积梯度;ρ为液压油密度。由式(9)和图1所示的功率键合图可得进入液压缸无杆腔的流量q15和流出有杆腔的流量q21:

当无杆腔进油、有杆腔回油时,R2和R3代表的阀口关闭,则液阻R2=R3= +∞;回油阻力很小,故令p8= 0,则由式(4),(5),(10)可得:

1.2 系统的数学模型
液压缸的状态方程可写为

比例伺服阀是以电压U为输入、阀芯位移xv为输出的二阶振荡环节,ω1和ξ分别为其固有频率和阻尼比,k1为二阶振荡环节的增益。因此用微分方程的形式可表示为

联立式(13),(14)可得系统以电压U为输入量、输出力F为输出量的表达式为
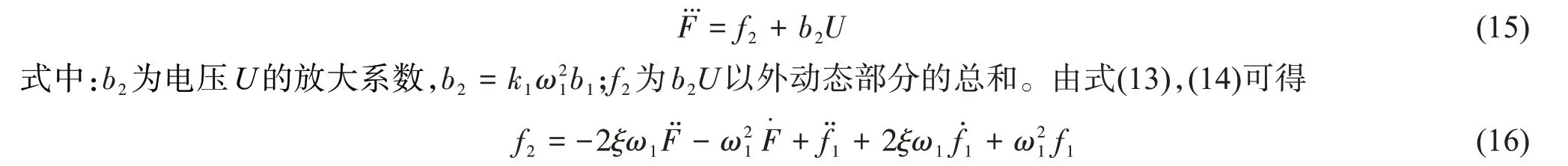
1.3 系统阶次的降低
由式(15)可知系统为三阶,由自抗扰控制原理可知需设计三阶自抗扰控制器,控制器中包含四阶扩张观测器和三阶跟踪微分器。同时需要三阶跟踪微分器产生指令的跟踪信号及其一阶和二阶微分信号,并与扩张状态观测器估计出的3 个系统状态变量进行比较,构成状态误差反馈。这样设计的自抗扰控制器结构复杂、控制器参数众多、难以整定,不利于实际应用,故需通过降低系统阶次来简化自抗扰控制器的设计。
文中结合打捆机电液系统中比例伺服阀作为已知二阶振荡环节的特点,采用系统零点配置法,通过增加1个跟踪微分器,产生1个可抵消比例伺服阀环节的二阶微分环节,其原理如图2。

图2 系统零点配置原理Fig.2 Principle of system zero point configuration
引入的跟踪微分器状态方程如式(17),u为控制器输出量;n1,n2,n3为跟踪微分器的状态变量。在选取速度因子r足够小的情况下,n1近似等于u,相应的n2和n3分别近似为u的一阶和二阶导数;再通过n1,n2,n3线性组合近似构造二阶微分环节,如式(18)。
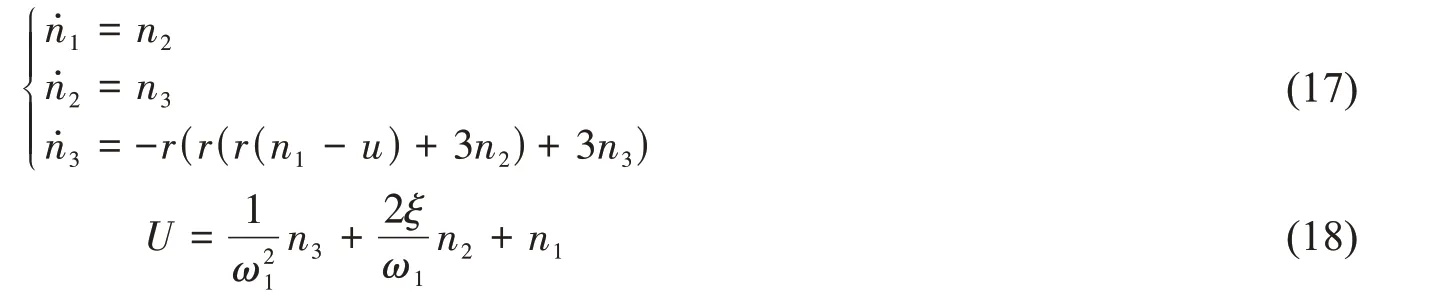
通过零点配置,抵消比例伺服阀的动态特性,系统为

再以力传感器输出量y为系统输出时,由式(18)可得

式中:b3为控制量u的放大系数,b3=k1k2b1;k2为代表力传感器的比例环节增益;f3为b3u以外动态部分的总和,f3=k2f1。
2 ADRC线材打捆机电液力控制系统的设计
自抗扰控制线材打捆机电液力控制系统的设计原理如图3。图3 中,β为期望与输出信号之间误差的反馈系数,g为未知外部扰动。通过将u和y作为扩张状态观测器的输入,估计出控制系统的总扰动,再对u进行实时补偿,抵消总扰动的影响。通过被控量y与指令信号a的误差反馈作用实现控制,其中自抗扰控制器由状态观测器、扰动补偿和误差反馈组成。

图3 ADRC系统原理Fig.3 Principle of ADRC system
2.1 扩张状态观测器
被控系统为一阶,所以设计二阶扩张状态观测器。二阶扩张状态观测器以控制量u和传感器输出量y为输入,其状态变量用z1和z2表示,分别代表对y和f3的估计值。

式中:e为估计值z1与实际值y的误差;b为放大系数b3的估计值;α1,α2为扩张状态观测器的参数,采用带宽ω1概念确定,分别取2ω2,。
2.2 误差反馈和扰动补偿
通过将扩张状态观测器对总扰动的估计值z2对输入u进行补偿,抵消总扰动,使系统变成输出y仅受输入u影响的积分串形式,再通过a和y的误差信号e0进行负反馈控制。误差反馈和扰动补偿为:

3 仿真分析
采用AMESim 和Simulink 软件对系统进行联合仿真。在AMESim 软件中建立线材打捆机电液系统模型,供油压力为200 Pa;无杆腔和有杆腔直径分别为160,110 mm;活塞及负载折算到活塞上的质量为8 150 kg;黏性阻尼系数为1 000 N·m-1·s;液压缸的内泄露系数为4×10-3L·min-1·Pa-1;比例伺服阀的固有频率和固有阻尼比分别为5 Hz,0.7;负载刚度为4×105N/m;力传感器的增益为1×10-5V/N。在Simulink 软件中搭建ADRC和PID控制器模型,通过加入白噪声(白噪声能量NP为0.1,1.0)来模拟外部干扰,以阶跃信号和正弦信号为指令信号,仿真分析干扰情况下基于ADRC和PID控制系统的动态响应和稳态跟踪性能。
3.1 动态响应
反馈控制率参数β= 20,扩张状态观测器带宽ω2= 100,放大系数估计值b= 0.2,用于零点配置的跟踪微分器参数r= 200,NP分别为0.1和1.0时ADRC和PID控制系统的动态响应曲线如图4。由图4可知:在对阶跃信号的动态响应过程中,NP较小(0.1)时,PID控制系统的响应时间为2.5 s,ADRC的响应时间仅1.2 s,同时PID 控制下液压缸输出力伴随较大的超调和振荡,最大超调为33.5%,而ADRC 下输出力几乎没有超调和振荡;NP较大(1.0)时,ADRC系统动态响应几乎不受影响,但PID控制系统动态响应性能变差,超调进一步加剧,最大达39.2%。

图4 NP为0.1和1.0时ADRC和PID系统的动态响应曲线Fig.4 Dynamic response curves of ADRC and PID systems when NP is 0.1 and 1.0
NP 为0.1 和1.0 时ADRC 系统总扰动估计曲线如图5。由图5 可看出:相较于PID 控制系统,ADRC 控制系统能较好地对总扰动进行实时估计,且通过对控制量的主动补偿使系统具有较强的抗干扰能力,有效提高了线材打捆机电液力控制系统在干扰下的动态响应性能。

图5 NP为0.1和1.0时ADRC系统总扰动估计曲线Fig.5 Total disturbance estimation curves of ADRC system when NP is 0.1 and 1.0
3.2 稳态跟踪性能
反馈控制率参数β= 200,NP 分别为0.1 和1.0 时ADRC 和PID 控制系统的稳态跟踪曲线如图6。由图6可知:ADRC控制系统对正弦信号的跟踪好于PID控制系统;在干扰较大(NP=1.0)时,ADRC控制系统稳态跟踪性能几乎不受影响,但PID控制系统稳态跟踪性能变差。
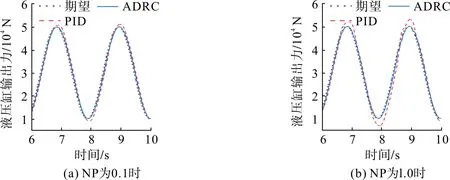
图6 NP为0.1和1时ADRC和PID系统的稳态跟踪曲线Fig.6 Steady state tracking curves of ADRC and PID systems when NP is 0.1 and 1.0
NP为0.1和1.0时ADRC和PID控制系统跟踪误差曲线如图7。分析图7可知:不同NP下,ADRC控制系统相对跟踪误差都维持在2.4%以内;对于PID 控制系统,NP 较小(0.1)时相对跟踪误差为7.9%,NP 较大(1.0)时相对跟踪误差增至10.8%。由此可看出,ADRC控制系统具有更好的稳态跟踪性能,抗干扰能力更强,打捆机在干扰条件下依然保持较稳定的打捆力。
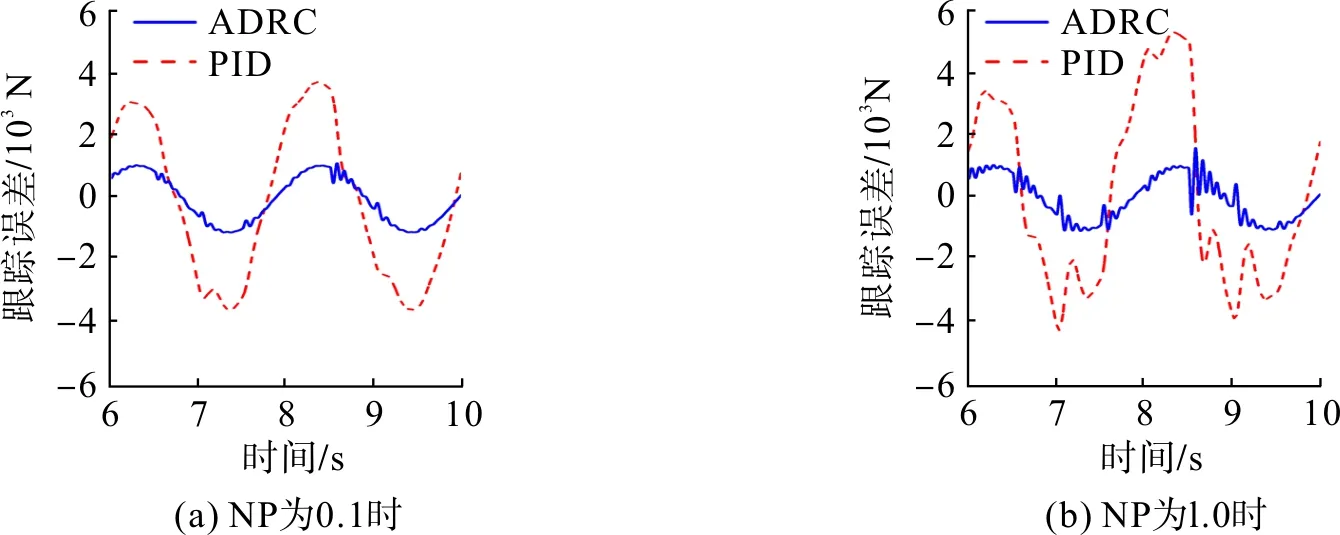
图7 NP分别为0.1和1.0时ADRC和PID系统的跟踪误差曲线Fig.7 Tracking error curves of ADRC and PID systems when NP is 0.1 and 1.0
4 结论
针对PID 线材打捆机电液力控制系统控制性能不佳的问题,设计基于自抗扰控制(ADRC)的线材打捆机电液力控制系统。通过功率键合图法对线材打捆机阀控缸液压系统进行数学建模;根据系统中比例伺服阀为二阶振荡环节的特点,通过配置其零点的方法降低系统的阶次,简化自抗扰控制器的设计。仿真结果表明:与PID 控制相比,在同一外加干扰情况下ADRC 系统阶跃响应时间缩短了50%,动态过程无超调、更平稳,稳态跟踪时误差减小到2.7%,ADRC 系统具有较好的动态性能和稳态跟踪性能;在加大干扰的情况下,ADRC 系统控制性能基本保持不变,表现出较好的抗干扰能力和鲁棒性。设计的ADRC 线材打捆机阀控缸液压系统能有效提高打捆机的打捆质量,可为系统的工程应用提供参考。

