几何视角直观，代数视角运算——一道离心率的探究

雷建荣

(环县第一中学，甘肃庆阳，745700)

涉及圆锥曲线的离心率的求值或取值范围的确定等相关问题，是每年高考试卷中的常见类型，此类问题创新新颖，变化多端，可以有效实现圆锥曲线与其他相关数学知识的交汇与融合，充分体现高考命题“在知识交汇点处命题”的指导思想，是数学命题的一种灵活变换与应用．

1 问题呈现

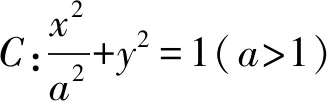
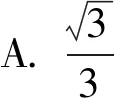
2 问题剖析

此题是一道涉及椭圆的离心率的求解问题，结合椭圆上一点与两焦点所角成的大小，以及该点到原点的距离这两个条件来合理构建．此类问题是近年高考数学试卷中的一个考查热点，主要考查圆锥曲线的相关知识、直线与圆锥曲线的位置关系等，交汇并融合平面几何、三角函数、不等式的性质等相关内容．

解决此类问题的一般思路有以下两种：

(1) 几何角度，借助平面几何知识，数形直观，结合圆锥曲线的图形，尝试寻找图形中蕴藏的几何关系，进而加以直观推理与求解．

(2) 代数角度，借助圆锥曲线上的点的坐标等相关知识，通过公式等巧妙寻找关于角或者边的函数或不等关系等，进而加以数学运算与求解．

此类问题解决时思维多样，策略多变，技巧多样，解决问题时或一种策略独领风骚，或多种策略齐心协力，或另辟蹊径，合理转化，巧妙破解．

3 问题解决

思维角度一：几何角度

方法1：(中线向量法)

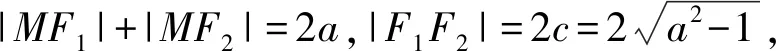
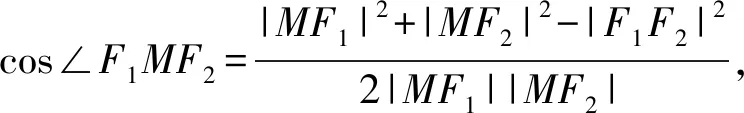
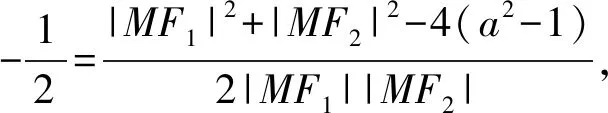
则有|MF1||MF2|=4，

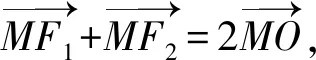
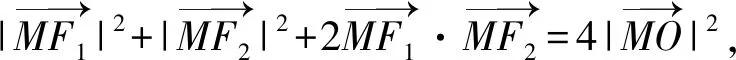
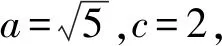
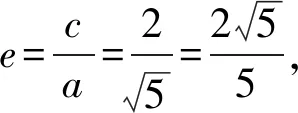
方法2：(中线长公式法)

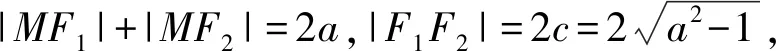
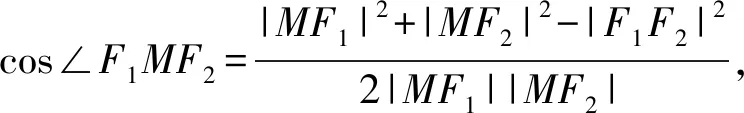
则有|MF1||MF2|=4，

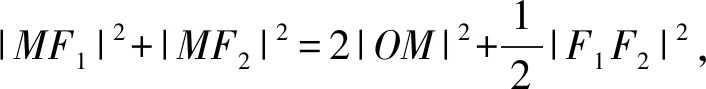
整理可得(|MF1|+|MF2|)2-2|MF1||MF2|=4+2(a2-1)，即4a2-8=4+2(a2-1)，

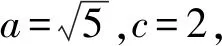
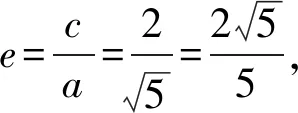
方法3：(余弦定理法)

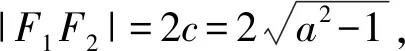
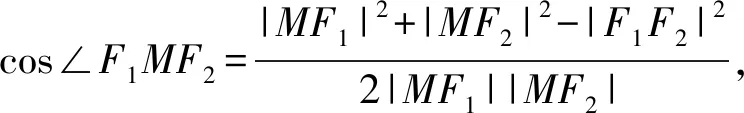
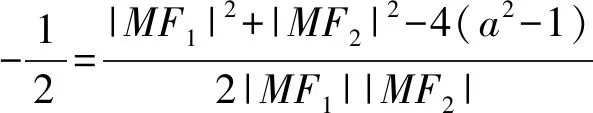
整理①②可得|MF1|·|MF2|=4 ③，

在△OMF1和△OMF2中，cos∠MOF1=-cos∠MOF2，

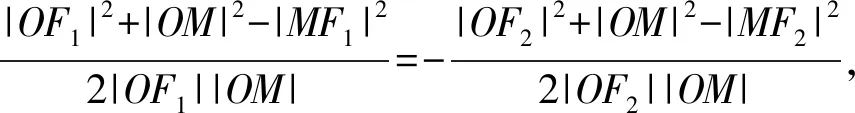
整理可得|OF1|2+|OM|2-|MF1|2=|MF2|2-|OM|2-|OF2|2，即|MF1|2+|MF2|2=2c2+4=2a2+2，

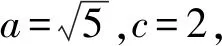
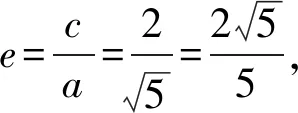
方法4：(极化恒等式法)

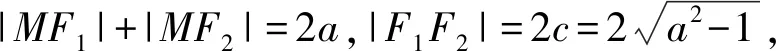
整理可得(|MF1|+|MF2|)2-2|MF1||MF2|=4+2(a2-1)，即|MF1||MF2|=a2-1，

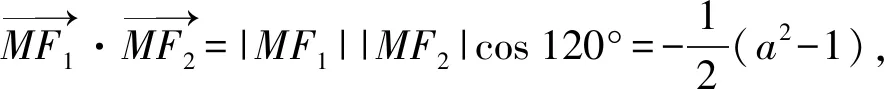
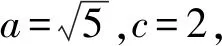
方法5：(焦点三角形面积法)

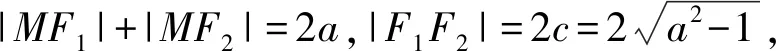
整理可得(|MF1|+|MF2|)2-2|MF1||MF2|=4+2(a2-1)，即|MF1||MF2|=a2-1，

在焦点三角形F1MF2中，由于∠F1MF2=120°，

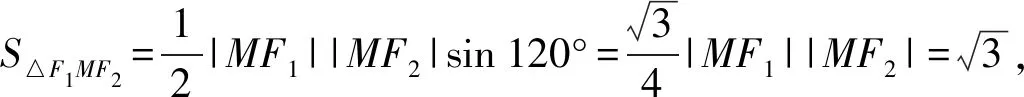
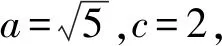
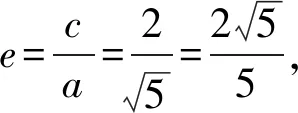
解后反思：绝大多数的圆锥曲线的离心率问题都可以运用几何法来分析与求解，几何法是求圆锥曲线的离心率的快捷方法．通常根据题中的图形特征，构建合适的三角形，借助正弦定理、余弦定理等解题．几何法一般计算简便，数形直观，备受学生青睐．以上问题的核心就是三角形的两种几何关系处理：中线关系，三角形的边的关系．

思维角度二：代数角度

方法6：(设点法)

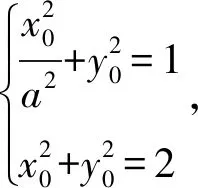
在焦点三角形F1MF2中，由于∠F1MF2=120°，

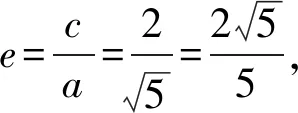
方法7：(焦半径公式法)

解析：设M(x0，y0)，由椭圆的焦半径公式可得|MF1|=a+ex0，|MF2|=a-ex0，

在焦点三角形F1MF2中，由于∠F1MF2=120°，

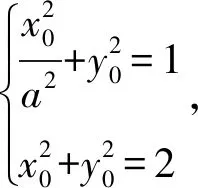
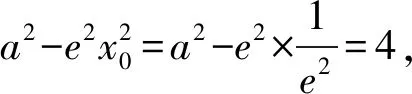
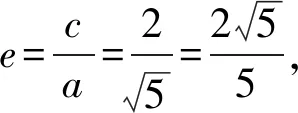
解后反思：求解圆锥曲线的离心率问题，利用代数角度去处理，核心就是确定相关点的坐标，通过坐标计算，转化到参数a，b，c的关系，进而求出相应的参数值以及对应的离心率．一般在无法应用相应的几何关系，或看不出几何关系的情况下，可以采取代数方法来分析与处理．

4 教学启示

4.1 规律总结，技巧策略

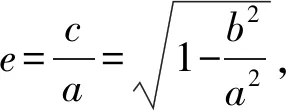
其中几何视角中，结合本题的三角形相关关系，中线关系可以用平面向量、中线长公式、邻角互补关系等来处理，三角形可以用余弦定理、焦点三角形等来处理，因而可以组合出众多的解法．而代数视角中，可以从坐标视角引入，结合焦点三角形面积公式来化归与转化，实现问题的解决．

4.2 思维深入，能力提升

涉及圆锥曲线中的相关问题，可以充分挖掘圆锥曲线自身的定义、方程、几何性质、结论与应用等，或从几何视角综合圆锥曲线的图象以及图形中点、线、角等元素之间的关系来处理，或从代数视角结合曲线方程以及函数与方程思想来处理，进而加以归纳、总结、类比、挖掘、探究，关键是构建圆锥曲线中相关参数之间的关系式，合理深入探究，从而全面提升数学思维方法、数学解题能力等，养成良好的数学思维品质，提高数学能力，培养数学核心素养．