基于有限元对农业污水脱离机机架轻量化设计

余浩，刘红梅,2，田俊杰，姚庆

（1.226019 江苏省 南通市 南通大学 机械工程学院；2.226019 江苏省 南通市 南通大学 交通与土木工程学院）

0 引言

农业生产中会产生大量污水、粪尿等固液混合物，为方便污水进一步处理以及粪污渣等用于干法发酵生产沼气，对固废液废水混合物处理需要用到过滤分离设备。带式压滤机是当前比较常见的污泥脱水设备和细颗粒物质固液分离设备，在煤炭、化工、造纸，特别在农业废水处理等领域应用广泛。压滤辊子是带式压滤机的主要组成部分，辊子是否有效工作是直接影响带式压滤机性能的重要因素之一。而机架是支撑辊子运动承载的主要部分，其强度、刚度对整机的运行影响巨大。当外部载荷超过极限强度时会导致机架发生形变甚至断裂。机架固有频率与外部激励频率处在同一范围时会引发共振，也会破坏机架结构[1]。本文采用有限元分析法对农业污水脱离机核心支撑部件——机架进行轻量化设计，以期优化机架结构，降低成本。同时，对轻量化机架的结构强度与外部激励进行仿真模拟分析，防止机架由于与外部激励源电机共振出现结构破坏。

1 静力学分析

1.1 理论介绍

通过静力学分析校核结构的刚度与强度是否满足使用要求[2]。依据经典力学理论，动力学表达式为

式中：[M]——质量矩阵；[C]——阻尼矩阵；[K]——刚度矩阵；{μ}——位移矢量；{}——速度矢量；{}——加速度矢量。

假设结构被完全约束，所受载荷随时间变化没有改变（或微小），并且这种情况下不考虑惯性力与阻尼，即：F（t）为常数，质量对结构不造成影响，阻尼对结构没影响，则式（2）可改写为[3]

在本文机架结构中，处于工作（运行）状态下的机架只受到各辊子和功能部件（轴承座）的重力与滤带张力作用，可采用式（2）的线性静力学分析。

1.2 仿真准备

1.2.1 三维建模与材料定义

依据CJ/T 508-2016《污泥脱水用带式压滤机》中的结构示意图（如图1 所示），通过SolidWorks软件搭建了带式压滤机机架三维图，如图2 所示。由于机架是组焊件，细微结构较为复杂，需要处理的细节较多，故建模过程中对某些结构特征如倒角、焊缝等未加以细化。这样的处理易于结构模型的生成，也可以提高计算效率。采用结构钢搭建的机架材料属性，具体定义见表1。

表1 材料定义Tab.1 Material definition

1.2.2 网格划分与载荷约束

机架长、宽、高分别为5 030，2 520，1 760 mm，将其组件均设计为U 型结构，厚度为10 mm，以增加机架的压力承受能力和更好的可安装性，延长使用寿命。采用10 mm 的网格划分，同时选择自动网格划分形式，生成的网格图如图3 所示。

对于机架，载荷施加方主要为辊子及其支撑的功能部件，其辊子及功能部件质量见表2。在运行状态下，辊子除自身重力之外还受到滤带张力作用，故机架主要承受的载荷为自身重力、滤带张力和辊子重力的合力。而滤带对辊子缠绕包角不同，可分解为垂直方向载荷和水平方向载荷。依据包角，推出辊子所受分力计算结果见表3。添加约束是底部采取ANSYS Workbench 中自带的Fixed Supported固定支撑。

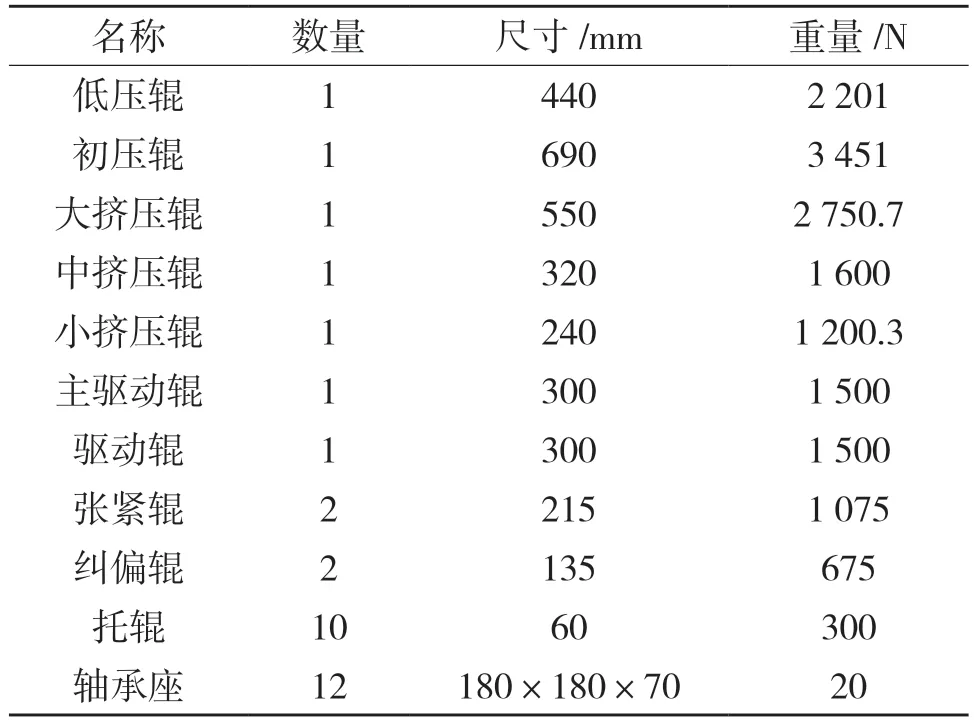
表2 辊子、功能部件尺寸及重量Tab.2 Dimensions and weight of rollers and functional components

表3 辊子所受张力分力Tab.3 Tension component of roller

1.3 结果分析

计算求解出空载和负载下的机架的应力、位移云图，分别如图4—图7 所示。由图4、图5 可知，空载状态下机架的最大应力为78.86 MPa，远小于屈服极限235 MPa，最大位移为0.82 mm；由图6、图7 可知，负载机架的最大应力为118.89 MPa，符合屈服极限要求，而最大位移为1.29 mm。造成这种差异的原因是滤带被张紧辊拉紧产生张力（4 kN）。

辊子被滤带包裹，张力在辊子表面产生周向摩擦力（施加于辊子转动）与径向力（施加于机架），导致空载状态与负载状态机架受载完全不同。运行状态中滤网张力与辊子重力相互叠加或抵消，引起机架各部位的载荷变化。2 种状态下的变形量对机架整体影响有限，并且应力冗余量都较大，优化时可考虑降低机架材料厚度，提升轻量化和降低动力输出，以更好地满足节能、低碳、环保的要求。

2 模态分析

2.1 理论介绍

为了更好地研究外部激励源对轻量化机架设计的影响，特别是电机频率对机架固有频率的干扰，采用模态分析的方法。ANSYS Workbench 的模态分析主要以结构的振动特性作为研究对象，从而获取机械结构的模态参数。其基本过程是将上述式(1)的线性时不变系统振动微分方程组中的物理坐标转换为模态坐标，使方程式解耦，成为一组以模态坐标及模态参数描述的独立方程，坐标变换的变换矩阵为振型矩阵，每列即为各阶振型[4]。

忽略阻尼与外力的影响，由式（1）可推出：

整个系统运动微分方程可分解为n 个表达式，可视作为2 阶常微分方程求解，可得：

将式（4）代入式（3），可得：

将式（5）两边同时除以sin（ωt+θ）可得：

对于式（6），{φ} 不可能为0，故

求解式（7），其特征值ω对应结构的固有频率，将特征值由小到大排序，0＜ω1＜ω2＜ω3＜…＜ωn。其中，i 对应的是第i 阶固有频率，特征值对应的特征向量对应结构的主振型，φ=[φ1φ2…φn]构成了结构的模态振型。

2.2 仿真准备与分析

2.2.1 模态分析的建立

为避免产生共振现象，需要确定结构的固有频率和振型，同时确定不同载荷条件下结构的共振形式[5]。任一零部件均有无限的振型，自由零件对应于6 个自由度（沿X 平移、沿Y 平移、沿Z 平移、绕X 轴转动、绕Y 轴转动、绕Z 轴转动），本文仅选取机架的前6 阶模态进行分析。机架的固有振动频率与前6 阶振型见图8，结果见表4。

2.2.2 结果分析

由表4 可知，机架的振型主要表现形式为弯曲与摆动，前6 阶频率最小为11.664 Hz,频率最大为27.084 Hz。机架频率符合随阶数上升而增加。这满足模态分析中无阻尼振动的随机性。

表4 前6 阶频率与振型描述Tab.4 Description of the first 6 frequencies and mode

机架的固有频率与激励频率的关系满足式（8）时，机架不会产生共振现象[6]。

式中：ω0——固有频率，Hz；ω——激励频率，Hz。

压滤机的激励频率源于其电机，机架固有频率范围11.664～27.084 Hz，与电机固有频率（50 Hz）不在同一频率范围，原有机架不会产生共振现象。

3 机架结构优化

3.1 优化前后对比

将机架的整体厚度由10 mm 减为5 mm，对比优化前后的应力、位移及质量和模态分析情况。优化后的应力、位移图见图9—图12。优化前后最大应力、变形和质量如表5，优化前后的振型与位移对比结果见表6。

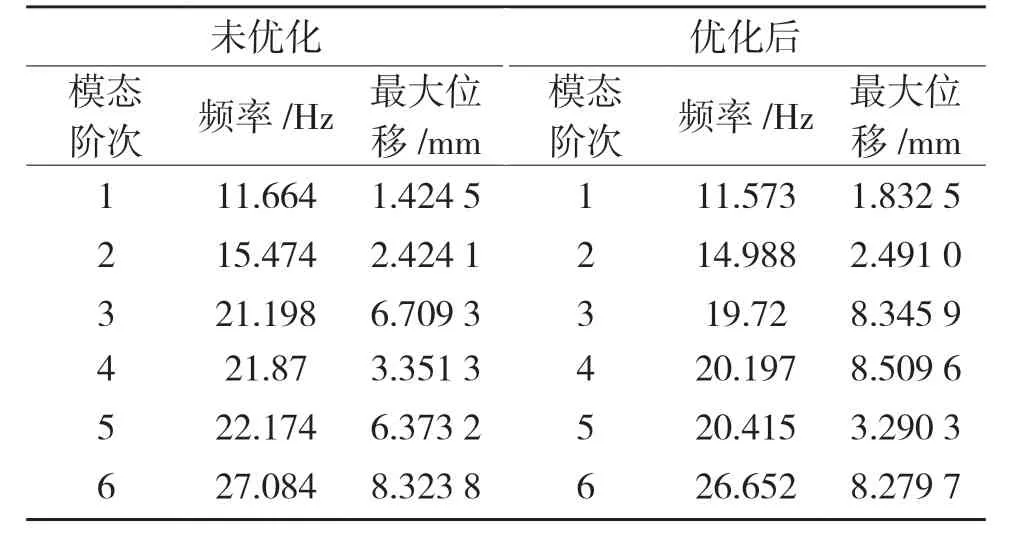
表6 优化前后振型比较Tab.6 Comparison of mode shapes before and after optimization

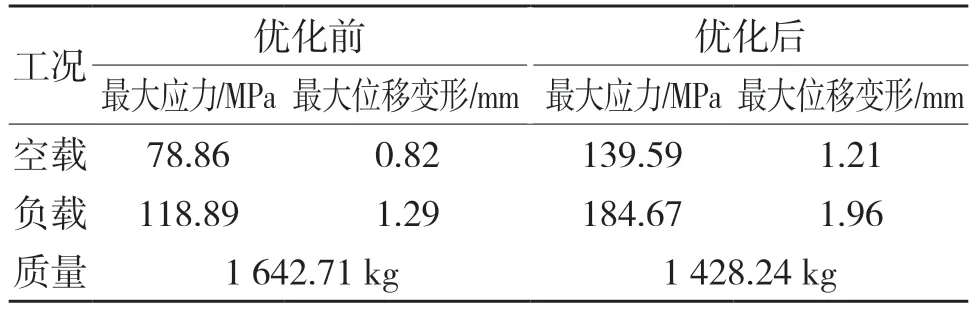
表5 优化前后应力、位移和质量对比Tab.5 Comparison of stress,displacement and mass before and after optimization

3.2 结果分析

优化后机架不同状态下的最大应力得到提高，使应力余量减少，虽然机架厚度的降低导致位移变形量变大，但仍属于设计安全范围内。同时，优化使机架质量减轻13.05%，降低生产成本和无用功耗，并且在模态分析下发现，机架的轻量化未引起其固有频率范围较大改变，电机频率也未对轻量化机架产生干扰，故电机不需要进行替换，而且大幅度降低成本。

4 结论

本文基于有限元法对农业污水脱离机—带式输送机机架在负载与空载状态下的结构受力分析，同时分析其在外部激励下是否发生共振现象。在满足机架结构安全、无共振的前提下，对其进行轻量化仿真模拟研究。结论如下：

（1）对农业污水脱离机—带式输送机机架进行有限元仿真发现其结构受力稳定，在空载状态下其最大应力为78.86 MPa，而负载状态下最大应力为118.89 MPa，均远小于机架材料定义的屈服极限235 MPa，说明机架材料应力余量较大，可进行轻量化。

（3）在对机架进行轻量化后，其运动状态下最大形变量由1.29 mm 变为1.96 mm，最大应力由118.89 MPa 提高到184.67 MPa，虽有上升但都小于材料屈服极限，符合安全指标。机架的质量减轻13.05%，大幅度节约了生产成本。

（3）对机架进行固有频率分析，分析其最大激励源为电机，对二者固有频率进行比较，发现轻量化后机架不会受到电机频率影响而产生共振现象，符合安全标准。

本文通过有限元法对机架产品结构进行了优化，对缩短研发周期有借鉴意义，为农业机械轻量化研制与改进提供思路。