谈“减负”背景下初中数学有效作业设计

张剑荣

(福建省连城县第三中学，福建龙岩，366214)

2019年12月，国务院中央适时印发减轻中小学负担的通知，让教师们对“减负”的重要性有了明确的认识，并开始在日常学习的过程中尝试为学生“减负”.所有学科适当减少布置作业的量，初中数学是一门以作业、练习为主的学科；是对数学知识的验证与巩固的需要；是数学课堂之外必须的延伸与补充，是巩固数学知识，提升学生运算能力，利用数学知识解决问题的必经之路；也是保证数学课堂效率的重要措施.在“减负”背景下，初中数学老师须身体力行，探索数学课堂教学与课后作业设计上的相关对策，在不降低教学质量的情况下，精选课后作业，优化作业，让学生通过少量训练便可达到教学要求.

1 “减负”的概念与教学现状

“减负”是减轻负担的简称，文中所讲“减负”二字的含义是减轻学生的课后作业的数量.社会上有人形容最重的“公文包”是学生每天所背的书包，每天要做的作业是当下的中学生；睡得晚、起得早的是当下的学生.现实问题是随着孩子年龄的增长，基础学科不断增加，每一门学科都需要一定量的练习，方能达到教学的要求，这种现状，不得不引起我们的深思.如何有针对性地减少数学作业机械重复，让“减负”真正落到实处.这不仅仅是中学教育工作者思考的问题，更是教育主管部门需要思考的问题.最好的减负其实是减少学科数量，能不能从小学或者是初中就进行细化，因材施教.

2 “减负”背景下设计初中数学有效作业的实例讲述

传统的初中数学教学课堂是老师按教材进度设计讲解相关的定义、概念以及数学思维方法，课下做相应的习题，巩固课堂上所学的知识.“减负”的背景下，要求老师创新教学方法与模式，从全科出发，综合整理，调控作业结构，切实减少作业总量.优化作业设计，由浅入深，分层次，构建与落实有效教学方法.“减负”的目的是为了更好地教育，保证教学的质量前提下，有针对性和时效性地布置作业.如：两点之间线段最短.数学老师可以把它归结为一类题型——将军饮马题型(求最值常用类型).有以下几种模型，讲解用红线标出，不作细讲.

例1直线l和l的异侧两点A、B，在直线l上求作一点P，使PA+PB最短.(如图1)

例2直线l和l的同侧两点A、B，在直线l上求作一点P，使PA+PB最短.(如图2)

图1

图2

例3点P是∠MON内的一点，分别在OM、ON上作点A、B，使△PAB的周长最小.(如图3)

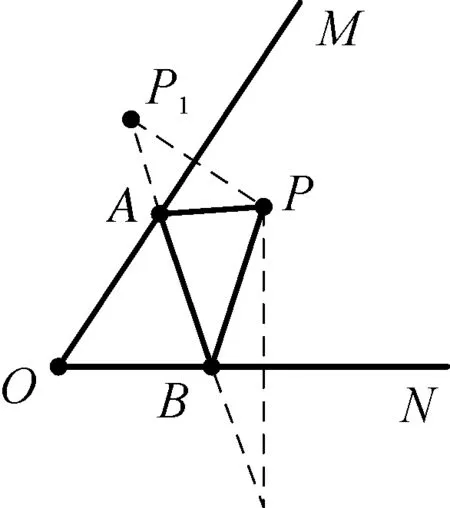
图3

图4

图5

例4点P、Q是∠MON内的两点，分别在OM、ON上作点A、B，使四边形PAQB的周长最小.(如图4)

例5点A是∠MON内的一点，在射线OM上作点P，使PA与点P到射线ON的距离之和最小.(如图5)

例6点A是∠MON内的一点，在射线OM上作点P，使PA与点P到射线ON的距离之和最小.(如图6)

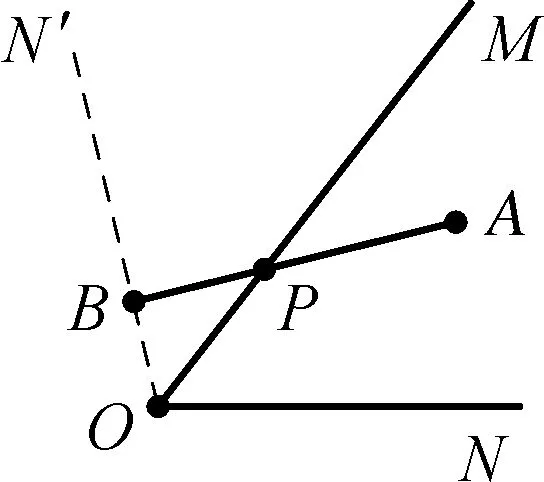
图6

以上六种类型，可以说将两点之间距离最小讲解得淋漓尽致，而且是由浅入深，符合学生思维和学习规律.有条件的老师可以做成动态图形，通过点的位置变化，形成不同的模型，更有利学生理解.然后根据上面的模型再布置适当的练习题，让学生仔细制订，巩固所学，做到举一反三，灵活掌握，最后实现学习致用.

3 因材施教，设计层次性和开放性作业

如果把人生比做小麦的生长期，那么中学阶段就是关键抽穗期.如果把人的一生比做一天，初中阶段则是刚刚升起的太阳，是最朝气蓬勃的时刻，是由幼稚逐渐走向成熟，身体逐渐长壮，争取独立意识的想法逐渐增强，学生容易越来越叛逆，不再依赖家长或老师，自己的事情要自己说了算.虽然同一学校的学生有相似经历，相近的习惯，但由于各自的智力水平、学习的能力，学习的习惯千差万别，他们所表现出的特长与才能也就不尽相同，数学老师在布置作业时可以因材施教，分层教学.让学生从感知认识、熟悉掌握、循序渐进、创造发挥、举一反三几方面考虑，可分三层布置作业.第一层模仿，相当于老师领着走.对这类同学要求学生熟悉教材内容，模仿教材例题，适当布置作业；第二层简单运用，要求这一类学生在理解教材内容、例题内容的基础上，对习题的条件进行合理变化，布置数量和难度都适中的习题，相当于跟着老师走；第三层，体现学生学习的综合能力，学生运用发散思维，对相应的知识融会贯通，训练思维的灵活性和深拓展性，相当于独立奔跑型.这三层没有明显的界限，让学生根据自己的能力去完成相应的层数.这样操作，可以最大程度地避免题海战术，同样让学生得到高质量学习成绩，既拓展了学生的数学思维，又减少中学生课业负担.同时可以系统地涵盖知识点以及变化形势，既可以照顾学生的差异性，又能做到层次分明，重点突出，作业不再单一枯燥，找到学习的乐趣，提升对做作业的积极性.

4 “减负”背景下初中数学有效作业设计的策略

4.1 前后融合，注重层次，总结知识点

笔者在讲完全等三角形判定所有定理后，进行相应的归纳总结.首先问学生，三角形有几个要素，全等三角有几个要素.学生乍一听，有点懵，回答的五花八门.最后我总结说，一个三角形有三个角(顶点)，三个边，共六大要素，全等三角形是取了其中三大要素对应相等，这样的定理有4个.学生听完，恍然大悟，如醍醐灌顶.趁热打铁，又问学生，那么全等三角形的模型又多少种呢.学生一一举例，最后老师给予补充说明，形成了以下几种模型.

(1) 平移型

(2) 轴对称型

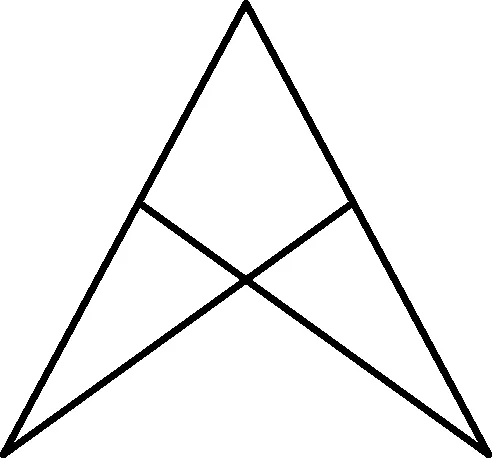
(3) 旋转型

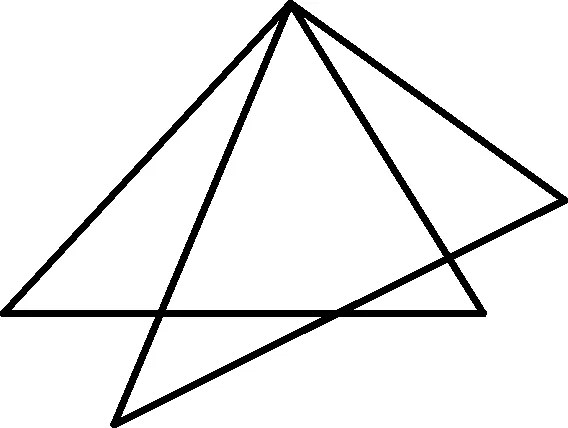
要求班上的每一位同学准备一个归纳总结本，每一节、每一章都进行一个归纳总结，当遇到相关模型时，就会有的放矢，迅速找到解题的突破口.

4.2 教师通过归纳总结，促进学生学习、思考

这种随时进行归纳的方法，是一种把厚书读薄的过程.既为学生节省了大量时间和精力，又为学生获取大的知识量创造了条件，提供了方法，同时激发学生主动积极进行，探讨、总结学习或做作业过程中的知识点.有事半功倍之效.

学生还可以根据自己学习的短板自主找相应作业习题来做，事先可以向老师报备，教师在布置作业时，可以不给该同学布置或少量布置.

4.3 结合中考题，归纳总结

对于初中数学，要求学生把每一次考试中，考得不好的地方标出来.间隔一段时间，2周或4周作一次总结.针对同样的题型，如果总是错，说明自己的知识点掌握不透，让学生自己去看教材，做相应的习题.然后自己总结出模型，吃透该知识.有一位同学说，当遇到K型图时，自己课下从多个角度画了K型图.但还总是掌握不熟练.而对于K型图，大小不一样，观察效果不同，只有多多观察，及时总结.“世事洞明皆学问，人情练达即文章.”通过以上细致的观察，并且抓住K型图的特点，才能一举攻克了这一题型.K型图模型如下：

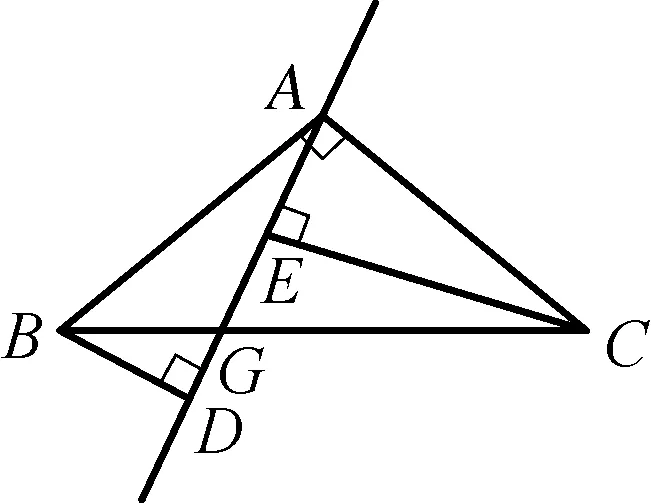
5 结语

“减负”的目的是为了更好地教育，而不是教育“减负”.教育是国之大计，民之大计，承载着继往开来的历史重任，肩负着为未来培养社会主义建设者与接班人的时代重任.“减负”是减掉中学数学不合理、不必要的负担，不是不要教学质量.通过“减负”，提升素质教育的实施，学习是艰苦的，需要付出艰辛的努力，“减负”的目的是增效，教师要通过改进教学方式，改变学生的学习方式，帮助学生养成良好的学习习惯，提高学生的学习的效率.