基于大数据的汽车驾驶员驾驶意图识别分析

闫伟，胥凌志，李嘉颀，王俊博，袁子洋

（250061 山东省 济南市 山东大学 能源与动力工程学院）

0 引言

车辆为人类社会提供了极大便利，在各领域发挥着重要作用，促进了世界社会和经济发展。根据驾驶员的驾驶意图，执行能量控制策略使驾驶员更有操作感，提高燃油经济性和排放性，因此驾驶意图识别是近年来的研究热点。现在前沿的驾驶意图识别模型包括隐马尔科夫模型、模糊控制器和神经网络等[1]。

将隐马尔科夫模型应用于汽车驾驶员驾驶意图识别领域，是1997 年由麻省理工学院的LIU 和PENTLAND 等提出的[2]。吉林大学的侯海晶[2]使用混合高斯隐马尔科夫模型和SVM 建立了识别模型，通过视觉特性推断驾驶意图的准确率在90%以上；北京科技大学的YAO YING[3]等人首先对特征向量进行聚类，然后通过隐马尔科夫模型进行迭代优化，按照安全性和环保型将驾驶风格划分为不同的驾驶习惯；山东科技大学的GUO[4]等人通过仿真实验，获得了视觉、听觉、嗅觉等动态数据，使用隐马尔科夫模型来建立意图识别模型，最终预测驾驶员的情绪转变准确性可达83%；山东大学的刘洋[5]通过建立模糊控制模型构建了混合动力汽车的能量控制策略并验证了该控制策略能够提升整车性能；王姝[6]等人使用支持向量机递归特征消除得到的特征向量构建了基于长短时记忆的转向意图识别模型，并证明了该模型能够有效改善汽车稳定性。

本文首先分析了驾驶意图特征识别参数，进行实车数据采集，对采集数据进行滤波等数据处理。然后分别对加速、制动、转向和驾驶风格的特征参数进行模糊C 均值聚类（Fuzzy C-means Clustering，FCM），并依据聚类结果建立隶属度函数和模糊控制规则。

1 数据采集和处理

1.1 实验设备及仪器

选定加速、制动和转向数据作为驾驶意图特征参数。使用型号为丰田系列89510-47040 的制动踏板行程传感器采集制动数据，如图1（a）所示。使用型号为丰田系列的89245-02030 的转向盘角度传感器采集转向盘转角，其测量精度为1.5°，如图1（b）所示。使用PCAN-USB 采集CAN 总线的加速踏板行程等数据并实时显示。

图1 实验设备Fig.1 Experimental devices

1.2 数据处理及分析

根据驾驶经验丰富且驾驶风格不同的驾驶员采集的数据，使用1.1 节中所述传感器获取实验数据并显示，其具有分时段（早、中、晚），分地段（市区、市郊、高速）的特点。

由于加速踏板行程、制动踏板行程和转向盘转角的传感器信号具有噪声，使用巴特沃斯滤波器对数据进行滤波，在除去高频噪声的同时保留体现驾驶员操作的秒级波动[3]。将数据随时间从0 附近变化为正值再变化为0 附近的区间识别为一次加速（制动、转向）过程，可得出此次过程中的数据平均值和数据平均值随时间的变化率，如图2—图4 所示。由图2 可知，加速踏板行程大部分处在0%～15%之间，在少数情况下加速踏板行程大于20%，加速踏板行程区间变化率大部分位于每秒0%～5%之间。由图3 可知，制动踏板行程多数集中在20%～40%之间，制动踏板行程区间变化率多数集中在20%～50%之间。由图4 可知，转向盘转向多数为小幅度转动且转向盘变化率多数位于0～50°/s 之间。

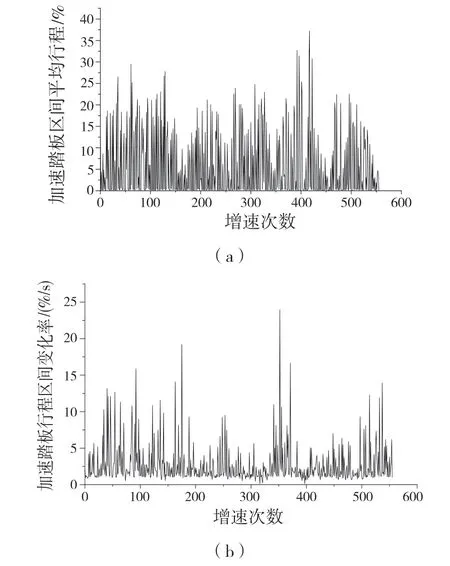
图2 加速数据Fig.2 Speed up data

图3 制动数据Fig.3 Braking data

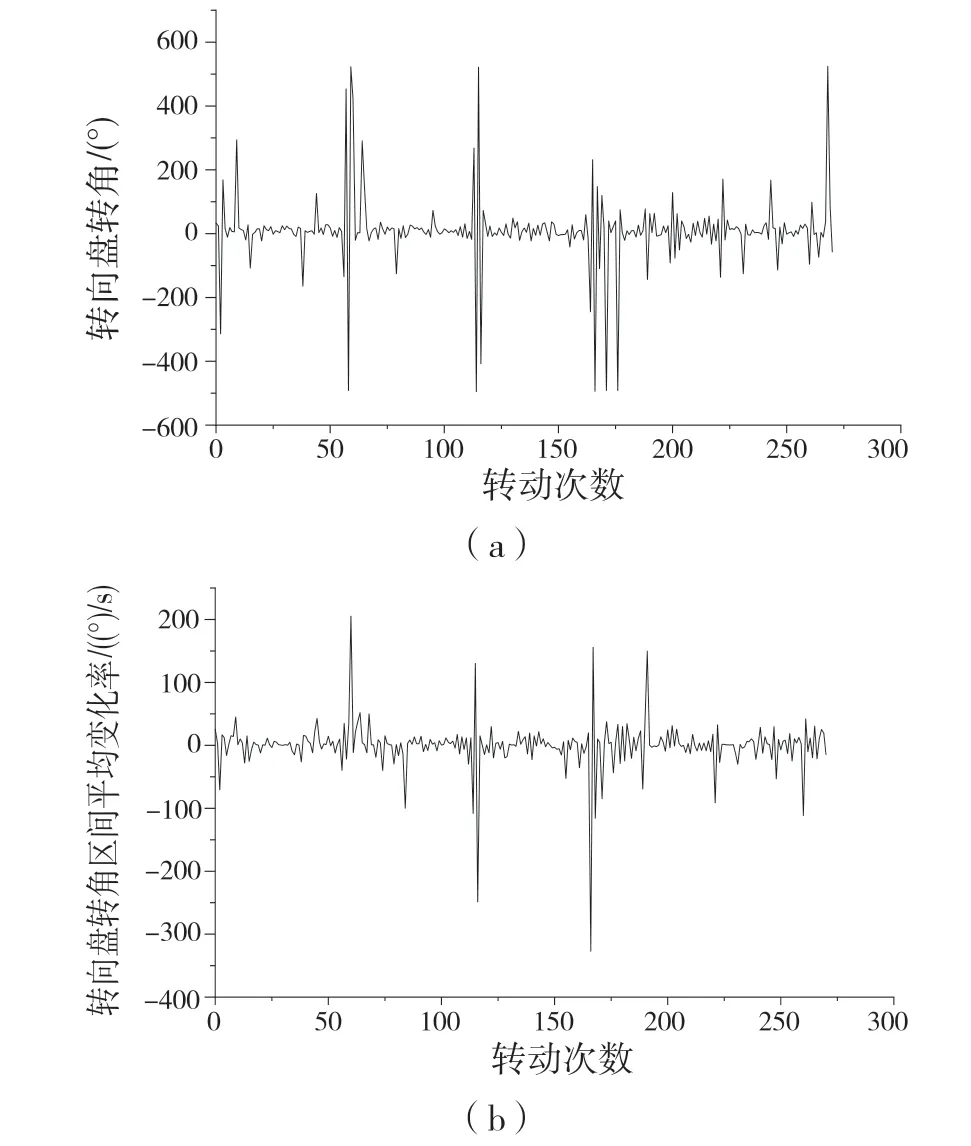
图4 转向数据Fig.4 Steering data

2 驾驶意图识别分析

模糊控制理论的基本思想是在进行控制决策时，首先将输入的信息转化为模糊概念，即确定概念的内涵，概念的具体外延模糊（具体数量），通过对输入值模糊化处理为模糊概念值，根据模糊控制规则计算，最后解模糊得到输出，最后传入控制策略执行机构实现被控对象的控制[7]。加速踏板、制动踏板的行程等大小判断属于模糊概念范畴，在大部分工况下不能简单地根据数值范围分类为大或小，因此使用FCM[8]对加速踏板行程、制动踏板行程、转向盘转角等数据进行聚类分析，为下文建立模糊识别模型提供理论基础。

FCM 的基本思路是将n个特征向量划分为c个聚类中心，然后根据隶属度和聚类中心计算损失聚类函数并不断迭代计算隶属度和聚类中心，最后使聚类损失函数Jm达到局部最小值。

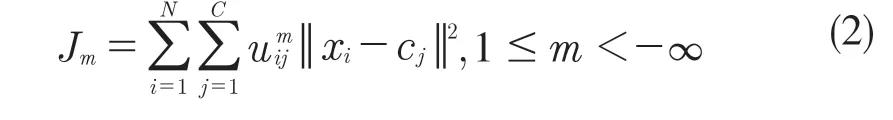
式中：N——特征向量数；C——聚类中心数，xi——第i个特征向量，cj——第j个聚类中心，uij——xi对于cj的隶属度。计算出xi和cj的直线距离，m表示迭代次数。

2.1 基于实测数据的驾驶意图聚类

对1.2 节中的数据进行标准化处理，然后使用R 语言的ppclust 库进行聚类。将加速、制动、转向和驾驶风格的数据分别作为特征向量，按第2 列数据升序排序，通过模糊C 聚类可以得到所有数据点分别对加速、制动、转向和驾驶风格聚类中心的隶属度，如图5 所示。由图5（a）可知，第3类隶属度在加速踏板行程区间变化率较低时占优，第2 类和第3 类在变化率中等时交替占优，在变化率较高时，第2类占优。由此可知第1类是中等加速，第2 类是快速加速，第3 类是缓慢加速。由图5（b）可知，第3 类隶属度在制动踏板行程区间变化率较低时占优，第2 类在变化率中等时占优，第1 类在变化率较高时占优。由此可知第1 类是快速制动，第2 类是中等制动，第3 类是缓慢制动。由图5（c）可知：前200 个数据点的第3 类隶属度均很高且波动较小，这是因为城市工况下大部分转向意图为变道和保持直行的意图。在第250 个数据点附近第2类隶属度较高，此时的驾驶意图为正常转向。在最后的样本点区域第1 类隶属度飙升，此时的驾驶意图为紧急情况转向或者掉头等意图。因此第1 类为快速转向，第2 类为正常转向，第3 类为缓慢转向。根据驾驶员的车速波动幅度，平均车速和转向半径可将驾驶员驾驶风格分为急躁型、沉稳型和谨慎型。由图可知，前250 个数据点第2 类隶属度最高，在第500 个到第1 500 个数据点之间第1 类数据占优。在第2 500 个数据点后第3 类隶属度占优，可知第2 类是谨慎型，第3 类是急躁型，第1 类是沉稳型。

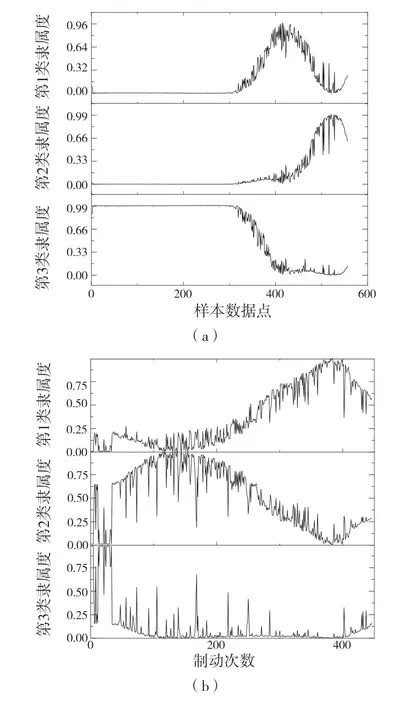
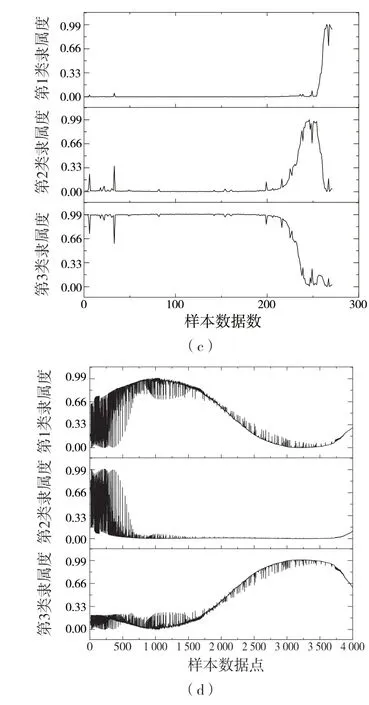
图5 聚类结果Fig.5 Clustering results

2.2 建立模糊控制器

由聚类结果分别确定加速、制动、转向和驾驶风格隶属度函数，并使用MATLAB 建立模糊控制器，隶属函数如图6—图9 所示。

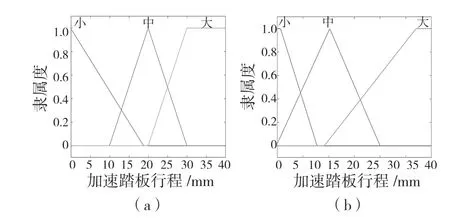
图6 加速意图隶属度函数Fig.6 Accelerated intention membership function

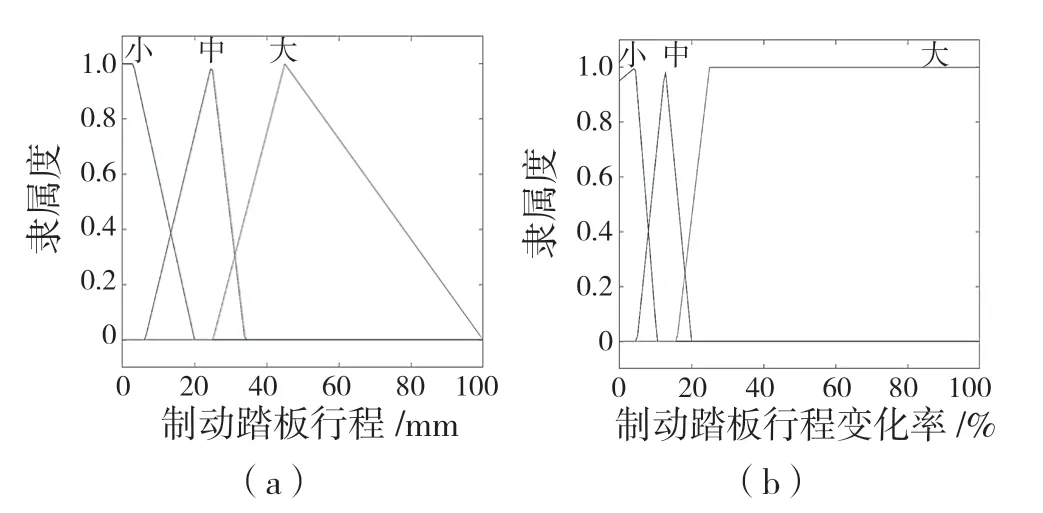
图7 制动意图隶属度函数Fig.7 Braking intention membership function

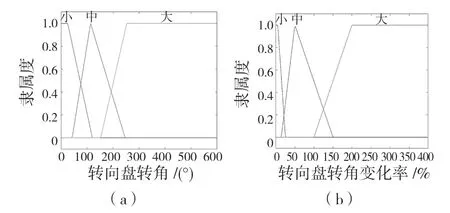
图8 转向意图隶属度函数Fig.8 Steering intention membership function

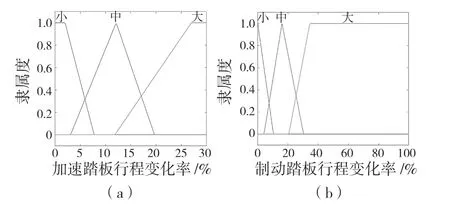
图9 驾驶风格隶属度函数Fig.9 Driving style membership function

确定模糊控制规则：首先对每个数据点根据隶属函数大小判断出特征向量的模糊值（小，中，大），然后根据聚类结果进行分类计数，取计数最多的类别作为该模糊规则下的识别结果，最终确定的模糊控制规则如表1—表4 所示。

表1 加速意图模糊控制规则Tab.1 Fuzzy control rules of accelerating intention

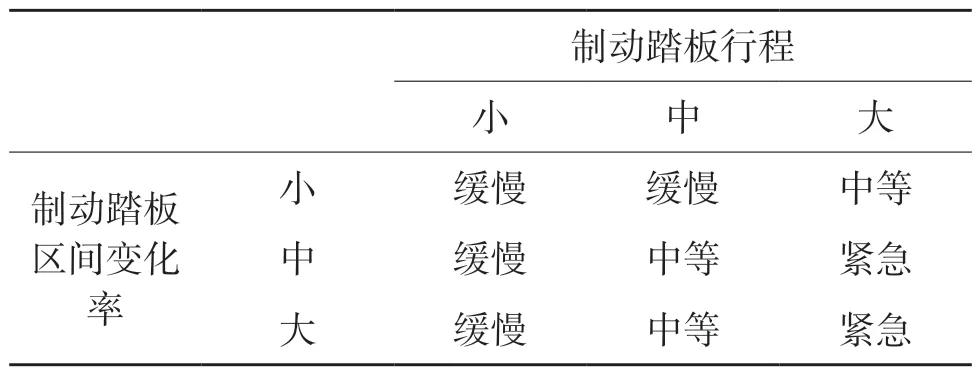
表2 制动意图模糊控制规则Tab.2 Fuzzy control rules of braking intention

表3 转向意图模糊控制规则Tab.3 Fuzzy control rules of steering intention

表4 驾驶风格模糊控制规则Tab.4 Fuzzy control rules for driving style

模糊控制器建立完成后，可得其输入输出值的三维视图，如图10 所示。

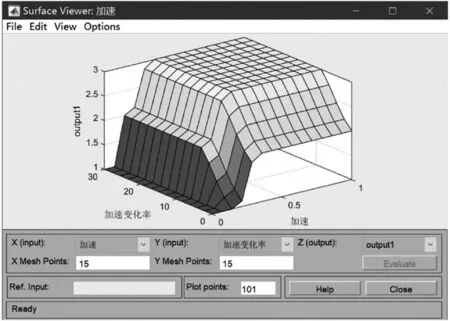
图10 三维视图Fig.10 Three-dimensional view

3 结论

为有效识别驾驶意图，分析了能够作为识别驾驶员操作意图的参数，然后通过嵌入式控制器进行实车实验，采集了与驾驶员操作意图相关的数据。将实验所得数据进行处理，分析出数据的集中区间和分布特征并初步确定数据的分类，使用模糊C 均值进行验证并为建立隶属函数提供依据。分析了模糊控制系统应用于驾驶意图识别的优点，根据模糊C 均值结果初步确定了隶属函数，并通过统计确定了模糊控制规则，最后使用MATLAB 建立了模糊控制模型，为下一步研究打下基础。