基于深度强化学习的蛇形机械臂控制策略研究
唐超,张帆,王文龙,李徐
(201620 上海市 上海工程技术大学 机械与汽车工程学院)
0 引言
随着科学技术的不断发展,机器人技术被广泛应用于社会的各个领域。蛇形机械臂由于具有多自由度、环境适应性强、结构细长等特点[1],在医疗器械、核电设备检修、航天航空制造和地震灾后救援等领域有着广泛的应用[2-5]。特别是在医疗器械领域,蛇形机械臂有着较大的发展空间。HU[6]等人设计了一种用于腹腔镜手术的基于线驱动机构的被动蛇形机械臂;WEI[7]等人设计了一种用于喉部微创手术的微型蛇形装置。
在蛇形机械臂控制领域,通常采用数学方法对其运动学和动力学方程进行研究。马影[8]等人提出了一种基于末端跟随算法的运动控制策略,该方法采用几何推导实现了蛇形机械臂末端的位置跟踪;王轸[9]等人提出一种基于脊线模态法和快速扩展随机树(RRT)的控制算法,实现了蛇形机械臂的避障轨迹规划。但由于蛇形机械臂结构的限定,机械臂通常涉及多个动作变量,从而使其模型更加复杂。并且由于自由度类型和外部不确定性干扰等因素,这些方法在不同的原型之间缺乏鲁棒性和可移植性。
近年来深度强化学习(Deep Reinforcement Learning,DRL)在机械臂控制领域逐渐兴起,并得到广泛应用。孙康[10]等人基于深度强化学习提出了一种空间漂浮基机械臂抓捕控制策略,实现对非合作目标的快速逼近和抓捕;刘钱源[11]基于深度强化学习提出了一种双臂机器人协同抓取策略,使双臂机器人能够成功地完成抓取物体的任务。上述研究表明,深度强化学习在多自由度机械臂逼近和抓捕问题上有较好的适用性,但是深度强化学习在蛇形机械臂控制领域还缺乏应用。
本文针对蛇形机械臂,提出了一种基于深度强化学习的控制策略。该策略使用深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)算法,通过设置奖励函数,实现了蛇形机械臂在2D 平面对目标物的快速精确逼近。该策略在不同的原型之间具有很大的可移植性,因为它学习独立于特定的蛇形机械臂模型。最后通过仿真实验在2D 平面验证了所学习的策略在控制过程中的适应性和鲁棒性。
1 基本概念
1.1 深度强化学习
深度学习(Deep Learning,DL)是机器学习的一种。深度学习的概念来源于人工神经网络的研究,具有多个隐藏层的多层感知器就是一种深度学习结构。深度学习是通过建立神经网络来模拟人脑解决问题。强化学习(Reinforcement Learning,RL)也是机器学习的一种,是关于一个主体与环境的相互作用,通过反复试验,在自然科学、社会科学和工程的广泛领域中为顺序决策问题学习一个最优策略。深度学习感知能力强,但缺乏一定的决策能力;而强化学习具有较强的决策能力,但没有办法处理感知问题。深度强化学习将深度学习的感知能力和强化学习的决策能力相结合,可以直接根据输入的图像进行控制,是一种更接近人类思维方式的人工智能方法。
1.2 深度确定性梯度算法
DDPG 是Lillicrap 等人[12]提出的包含价值网络和策略网络的算法,该算法包含了深度Q 网络算法(Deep Q Network,DQN)和演员-评论家算法(Actor-Critic,AC)的优点。在强化学习领域,DDPG 算法是从PG(Policy Gradient)[13]、DPG(Deterministic Policy Gradient)[14]、DDPG(Deep Deterministic Policy Gradient)一路发展而来的。
DDPG 是一种基于Actor-Critic 框架的确定性策略梯度的无模型算法,其学习过程如下:
(1)根据当前的策略和探索过程的随机噪声选择应执行的动作(action):

在环境中执行动作at,环境将给出一个新的状态st+1并返回奖励值rt;
(2)将状态转移的(st,at,rt,st+1)存储在replay buffer 中,并随机采样N组数据(si,ai,ri,si+1)。
(3)设置关于价值函数的目标值:

(4)更新Critic 网络:

(5)更新Actor 网络:
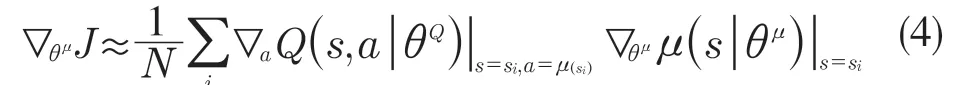
(6)更新目标网络
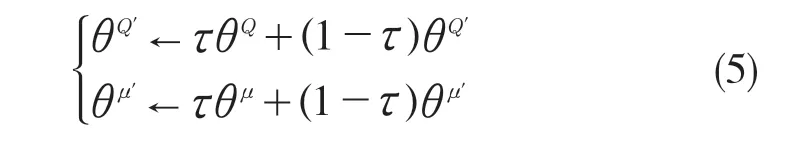
2 基于深度强化学习的蛇形机械臂的控制
2.1 深度强化学习
系统包括深度强化学习算法和实验仿真2 个部分[15],系统通过深度强化学习对神经网络进行训练,使得DDPG 算法可以控制蛇形机械臂抵达目标物。实验仿真部分的环境包括蛇形机械臂和目标物两部分,搭建仿真环境,环境接收算法的控制变量使蛇形机械臂产生相应的运动,然后将运动后的环境信息传递给深度强化学习算法,根据接收的环境信息,深度强化学习获得状态变量和奖励值[16],通过状态变量计算蛇形机械臂的控制量,通过奖励值更新深度强化学习中神经网络的参数。
2.2 蛇形机械臂模型
本文所采用的蛇形机械臂具有4 个蛇形机械臂单元,它们通过具有 2 自由度的万向铰链相互连接。每个蛇形机械臂单元长为72 mm,外径为55 mm,上下万向铰链距离为95 mm,如图1 所示。

图1 相邻关节的偏角姿态Fig.1 Deflection posture of adjacent joints
由于相邻蛇形机械臂单元空间有限,万向铰链的旋转角度受到一定的限制。在万向铰链旋转角度的计算中,本文将相邻关节轴线的交点作为原点,旋转角度关系如图2 所示。

图2 万向铰链的最大转动角度Fig.2 Maximum rotation angle of universal joint
由几何关系可知,万向铰链可转动的最大角度与相邻关节之间的垂直距离D和蛇形机械臂单元外径L的数学关系如下:

最后求得万向铰链可转动最大角度θw=45.3°
2.3 奖励函数
在深度强化学习中,奖励reward 表示某一个状态所产生的某一个动作对达到目标有多大贡献的评价[17]。深度强化学习算法通过奖励函数输出的奖励reward 进行学习训练,同时奖励函数也涉及到算法的收敛问题,所以奖励函数的设计十分重要。
根据蛇形臂末端是否抵达目标物设置奖励函数r1为:

在训练过程中,某次训练蛇形机械臂末端抵达目标次数连续超过30 次时,才视为完成此次训练,每抵达目标物一次奖励函数r1均运算一次。
结合蛇形机械臂的环境,奖励函数还包含目标物和蛇形机械臂末端的位置信息。目标物位置为(xgoal,ygoal),蛇形机械臂末端的位置为(x4,y4)奖励函数为r2:

最终确定奖励函数R:

2.4 状态state
在训练过程中,较全的蛇形机械臂状态信息会加快收敛速度。对于2D 末端执行器定位任务,状态信息由机械手末端执行器相对于目标的相对位置定义[17]。而对于本文所采用的蛇形机械臂,传统位置定义的状态信息难以满足快速收敛需求。本文将状态信息表示为:每一个蛇形机械臂单元末端相对于目标物和中心点的相对位置,4 个蛇形机械臂单元16 个状态信息,及蛇形机械臂末端是否在目标物上(如是返回值1,如果不是返回值0),共17 个状态信息。17 个位置信息保证了控制精度,也使得收敛速度大幅提升。
2.5 动作action
动作设计实质上属于运动规划范畴,是根据目标物体的位置控制机械臂的各关节运动,进而使机械臂末端执行器到达目标物体位置[18]。本文采用的蛇形机械臂共有4 个蛇形机械臂单元,每个单元在2D 空间均可左右转动45°,即转动范围为[-45°,45°],每个关节每次转动的角度在[-45°,45°]中随机选取一个值。
3 仿真实验与结果
3.1 仿真实验环境
本文通过仿真实验来验证所提出方法的优劣。基于Python 语言,使用gym 中的pyglet 模块搭建了一个蛇形机械臂在2D 空间的运动环境,整个环境如图3 所示。本文在2D 空间中用矩形代替3D空间中的圆柱形蛇形机械臂单元。该蛇形机械臂是由4 节蛇形机械臂单元串联组成的,其中每节蛇形机械臂单元可以分别向左、向右转动45°。其目标是通过深度强化学习,在蛇形机械臂的工作范围内使蛇形机械臂的末端抵达目标物,即使第4 节蛇形机械臂单元的顶端抵达灰色正方形区域。

图3 蛇形机械臂仿真环境Fig.3 Snake-like arm simulation environment
3.2 实验设置
本文使用在深度学习领域使用较为广泛的框架TensorFlow 来搭建用于训练蛇形机械臂的深度强化学习算法DDPG,使用matplotlib 模块可视化实验结果。深度强化学习的网络共包含2 个全连接层,网络的输入为蛇形机械臂的状态(state),输出为蛇形机械臂的动作(action)。为保证模型的鲁棒性,在蛇形机械臂每一个episode 后,将蛇形机械臂的初始位置设置为随机。4 节蛇形机械臂单元的臂长和臂宽均为95 个单位和24.5 个单位,并且可以分别向左、向右转动45°。
本文设置的DDPG 训练参数为:最大迭代次数(MAX_EPISODES)为600,每次迭代的最大步数(MAX_EP_STEPS)为300,actor的学习率为0.001,critic 的学习率为0.001,奖励折扣值为0.9,内存容量为30 000,每一个batch 的大小为32,神经元的个数为300。当某次训练时蛇形机械臂末端抵达目标次数连续超过30 次时,则视为完成此次训练。
3.3 结果分析
由图4 可见,仿真实验过程中学习初期属于探索阶段,蛇形机械臂在不断地探索环境,不断地收集环境的样本数据,难以抵达目标物。使其奖励值较低,并且每个episode 所采取的step 较多。在学习中期,由于样本数量的不断积累,动作策略与奖励函数之间的关系被不断建立起来,蛇形机械臂从探索环境开始转变为利用环境,可以较好地抵达目标物,在130 次迭代后模型开始收敛。随着蛇形机械臂学习的不断深入,蛇形机械臂尝试开始自己调整运动趋势,使其以最少的step 抵达目标物。最终奖励值稳定在25 左右,step 稳定在30 左右。从奖励值和step 的变化趋势来看,模型符合要求。

图4 蛇形机械臂的学习过程Fig.4 Learning process of snake-like arm
经过学习之后,为了测试学习过程的有效性,我们在蛇形机械臂的工作范围内随机选择一个目标(520,420),然后进行了2 组实验。第1 组实验使蛇形机械臂分别向上、向下各移动2 次,每次移动10 个单位。第2 组实验使蛇形机械臂分别向左、向右各移动2 次,每次移动10 个单位。并且我们希望蛇形机械臂最终能在目标物上连续停留至少30 次,最终测试结果如图5 和图6 所示,反映了蛇形机械臂的末端和目标物中心之间的距离通常随蛇形机械臂采取行动而减小,并且最终达到预期的效果。这些实验结果证明了我们控制策略的有效性。

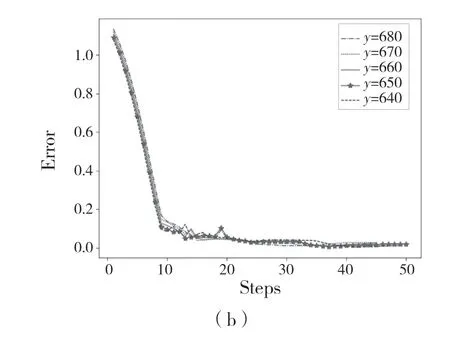
图5 蛇形机械臂以相同纵坐标分别向上、向下各移动2 次Fig.5 Snake-like arm moves up and down twice with the same vertical coordinate

图6 蛇形机械臂以相同纵坐标分别向左、向右各移动2 次Fig.6 Snake-like arm moves to left and right twice with the same vertical coordinate
3.4 鲁棒性测试
为了检验控制策略的鲁棒性,本文对蛇形机械臂进行了一些人工干扰,在每次的单独实验中分别对4 个蛇形机械臂单元进行了锁死,即不让该单元产生左右转动。同样,在蛇形机械臂的工作范围内随机选择一个目标(520,420),希望蛇形机械臂末端能抵达目标物,且在目标物上连续停留至少30 次。测试结果如图7 所示。

图7 分别对4 个蛇形机械臂单元进行了锁死Fig.7 Four snake-like arm units locked respectively
系统能够抵抗第2 节和第3 节蛇形机械臂关节锁死产生的扰动,蛇形机械臂仍然能够顺利到达目标物。在锁死第4 节蛇形机械臂关节的实验中,虽然蛇形机械臂末端不能在目标物上连续停留至少30 次,但蛇形机械臂末端在该关节锁定的情况下仍能抵达目标物,并且最终停留在目标物附近。在锁死第1 节蛇形机械臂关节的实验中,扰动已经超过了系统的容差。该策略只是相对有效的,因为目标物已经超出了蛇形机械臂的工作范围。蛇形机械臂试图接近目标,达到极限后保持不变。这些实验证明了我们控制策略的鲁棒性。
4 结语
本文在2D 平面提出了一种基于深度强化学习的蛇形机械臂控制策略。通过仿真实验表明了该方法在控制效果和鲁棒性上有不错的表现,同时它独立于特定的模型,具有较高的可移植性,能够移植到其他多自由度的机械臂上,如软体机械臂和基于折纸机构的连续体机械臂。
在今后的研究中,我们将添加更多的蛇形机械臂单元,考虑更多真实情况。比如避开障碍物,完成更复杂的任务。我们还会将该方法扩展到3D 空间的控制问题上,并考虑使用多个蛇形机械臂协同配合完成多目标任务。

