激活初中数学经典,提升数学核心素养
文/中山市小榄镇菊城中学 杨智明
研究课标、考纲、教材是教师日常备课的重要一环.作为一线数学教师,我们不喜欢加班加点,要让课堂有实效,充分利用好堂上时间培养学生的数学核心素,还要突破过去单一、枯燥、无趣的刷题式的课堂教学模式,激起学生的学习热情.教师必须要在课堂准备阶段先跳进题海,选取适当的具有代表性的母题,通过合理的设计引导并带领学生总结构建数学模型,通过分析对比提升逻辑推理素养,实现让学生跳出题海,在数学课堂上让学生的数学核心素养得到培养,使得课堂更具实效.
一、激活经典母题,抽象归纳,提升直观想象和建模素养
初中数学人教版教材九年级下册解直角三角形中有这样一道典型的例题:
题目1:如图1热气球的探测器显示,从热气球底部A处看一栋高楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球A处与高楼的水平距离为120m,这栋高楼有多高(结果取整数)?
解:如图2:过A作AD⊥BC,垂足为D.
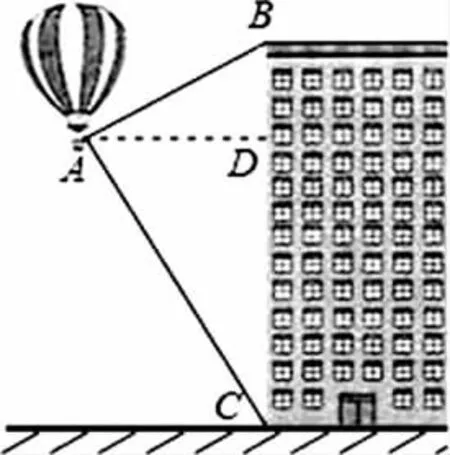
图2
在Rt△ABD中,∠BAD=30°,AD=120m,
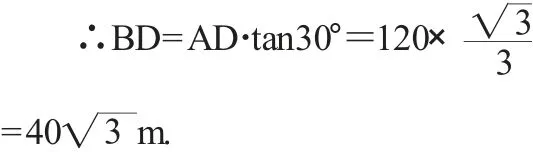
在Rt△ACD中,∠CAD=60°,AD=120m,

答:这栋楼高约为277m.
通过从以上经典母题我们可以发现∠BAC=90°,其中90°可以切割分为30°与60°的和,从而把一个角分割变成熟悉的两个特殊角,把一个三角形的问题转化为两个特殊直角三角形的问题来解决,通过此问题的解决可以归纳出解决此类题型一个模型是:分割其中一个角变成两个熟悉的具有特殊角的直角三角形的模型来处理.采用以上的模型分割的原理可以发现下面的两道题可以迎刃而解.
题目2:如图3,在△ABC中,AB=AC=2,∠A=90°,P为BC的中点,E、F分别是AB、AC上的动点,∠EPF=45°.

图3
(1)求证:△BPE∽△CFP.
(3)设BE=x,当E,F在运动过程中,∠EFP是否可能等于60°,若可能,请求出x的值,若不可能,请说明理由.
先撇开第(1)(2)问,直接看第三问:知道∠EPF=45°,若∠EFP=60°时,由三角形内角和可知∠FEP=75°,过点E作EM⊥PF,可以把75°角可分割成45°与30°的和(如图4),这样把原来非直角三角形就分割成两个具有特殊角的直角三角形,问题迎刃而解.
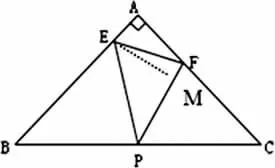
图4
题目3:从一幢建筑大楼的两个观察点A,B观察地面的花坛(点C),测得俯角分别为15°和60°,如图5,直线AB与地面垂直,AB=50米,试求出点B到点C的距离.(结果保留根号)
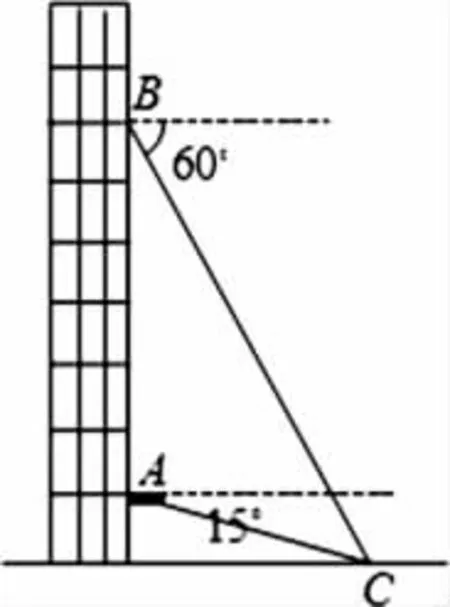
图5
由已知条件可得∠BAC=105°,过点A作AD⊥CB,可把105°可以分割成45°与60°的和(如图6),问题同样迎刃而解.
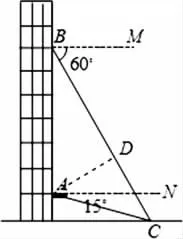
图6
上面两道题目结合经典母题来看,发现都与经典例题的模型一致:90°角可以分割成30°与60°角的和,75°角可以分割成45°与30°角的和,105°可以分割成45°与60°角的和.通过教材经典母题的激活,构建模型得出解决解直角三角形同类型题目普遍适用的模型,直观、易理解,既加深了学生的直观想象,又培养了学生对数学建模的理解,让数学的核心素养在课堂中得到渗透,提升课堂效率达到事半功倍的效果.
二、多层次激活经典母题,提高直观想象和数据分析素养
经历过初中三年循环教学的老师对下面的三个图形(图7)都相当熟悉,都是来自教材的经典的图形,同时我们对下面的题目4也是相当的熟悉,是广东中考试题.
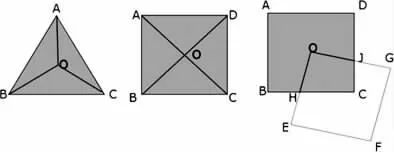
图7
题目4:(1)如图,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G.求证:阴影部分四边形OFCG的面积是△ABC面积的
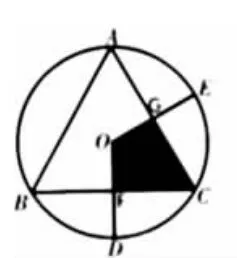
(2)如图8,若∠DOE保持120°角度不变.求证:当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC面积的
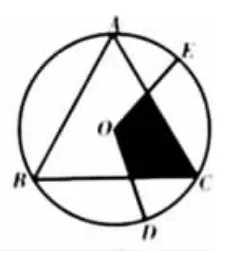
图8
笔者在一次参加中山市中考备考会议的时候,专家给大家呈现了上面教材的经典母题,通过类比变为圆内接正边形的问题便演变成我们所熟悉的中考试题,同时再次激活母题,通过圆的内接正多边形的原理让圆的内接正多边形的边数逐渐增加,基于母题的多层激活可以得到圆的内接正四边形、正五边形、正六边形……(如下图9-16)相关类型的题,针对基本母题的多层激活,直观的进行对比,通过改变数据,既培养学生的直观想象的素养,同时在改变数据的基础上让学生领悟数据的分析与处理,提升了学生的直观想象素养和数据分析素养.同时通过一道题目的方法总结得出解决此类圆内接多边形的模型.
三、激活经典母题,螺旋提升数学推理素养
我们再来看2019年广东中考试题的第19题作图题目:如图17:在△ABC中,点D是AB边上的一点.(1)请用尺规作图,在△ABC内,求作∠ADE,使∠ADE=∠B(不要求写做法,保留作图痕迹).(2)在(1)

图17
从题目命制的角度来看,考查的是八年级教材的经典母题:作一个角等于已知角的问题.但是此题除了常规的考察方法与模型外,由此引申出来的方法比较多.由其他的方法仔细分析不难发现命题者在考查学生的数学素养,老师在平常的课堂中是否落实了数学的核心素养.特别是最后的中考总复习过程中能否对知识点形成网络,能否再次唤醒并落实培养学生的数学素养.
(一)从模仿到变通——逻辑推理能力素养的形成
题目4(1)图
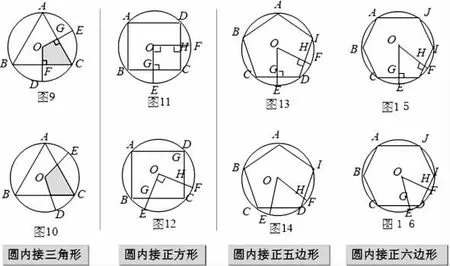
根据题目要求:求作∠ADE,使∠ADE=∠B,常规的做法已经形成了固定的模式是作一个角等于已知角,如下图(1):此法学生完全可以模仿老师课堂所教的基本作图方法完成.从完成的图形看来,逻辑推理能力好的学生不难发现由于∠ADE=∠B,可得DE//BC,那么从原理上来看,我们只需要作角后使得DE//BC即可!根据平行线的判定,除了同位角相等可以得到直线平行外,还可以由内错角相等得到两直线平行,因此可以得到第二种作图方法,如下图(2),利用内错角相等得到两直线平行,从而得到要求作的∠ADE=∠B.除了利用常规的方法以外还可以构建等腰△BDF,如图(3)作∠ABC的平分线,以点D为圆心,BD为半径画弧与∠ABC的平分线相交于点F,从而 可 得DE//BC,进 而 得 到∠ADE=∠B;如图(4)同样构建等腰△BDF可以得到等腰三角形顶角的平分线与底边平行,得到∠ADE=∠B,从而可以得到第四中作图方法.
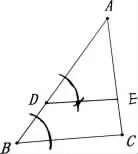
图(1)
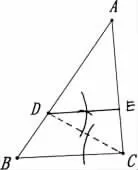
图(2)
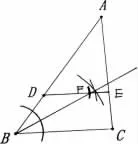
图(3)
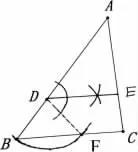
图(4)
不难发现以上四种作图均可以使得∠ADE=∠B,其中图(1)的方法只需要学生掌握老师课堂上讲的基本作图便可以作出来,但是要想学生用图(2)、(3)、(4)其中一种方法作出来,均要求有不同程度的逻辑推理:要想得到∠ADE=∠B,可以先得到DE//BC.通过逻辑推理,分析、寻找、作出平行线.基于图(2)、(3)、(4)的几种作图,要求老师课堂上注重基本方法的理解、掌握以及逻辑推理能力的训练,学生只有通过老师的引导在课堂上慢慢的积累沉淀下来,形成逻辑推理能力才能得出相关的作图方法!
(二)从变通到加深——逻辑推理能力再迈进一个台阶
从上面图(2)(3)(4)的几种作图发现都是通过逻辑推理的方法先得到平行,然后再由平行得到∠ADE=∠B.除了从角的关系得到平行,再由平行推导出角相等外,还可以通过构建平行四边形或特殊平行四边形的方法得到平行,再通过平行得到∠ADE=∠B.
其中图(5)以BD,BC为邻边作出平行四边形,由平行四边BCFD的对边平行得到DF//BC从而得∠ADE=∠B;图(6)以点B为顶点BD为边,作出菱形BDGF从而得到DG//BF,再得到∠ADE=∠B;图(7)先从点D向BC作垂线,截取线段DG使得DG=DF,再作线段GF的垂直平分线,相当于构造矩形或正方形得到DE//BC从而得到∠ADE=∠B.从以上的三种作图来看,要求学生不但对要想得到角相等,还先得到平行的一种逆向逻辑思维完全理解,还能联想到平行可以由平行四边形或特殊的平行四边形对边平行的性质得到,对逻辑推理的要求更高了,要求老师在平常的课堂上注重逻辑推理能力的深挖,比以上图(2)(3)(4)的几种情况对学生的逻辑推理能力迈进一个新的台阶.假如老师平常课堂上没有注重逻辑推理素养的理解,也没有注重让学生领悟各个知识点之间的联系,相信学生必定完成不出这样的图形.
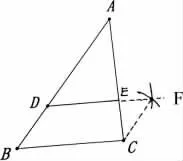
图(5)

图(6)
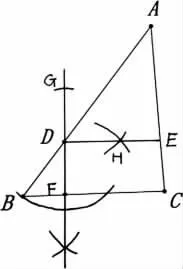
图(7)
(三)从加深到跳跃——逻辑推理能力的升华
图(7)从点D向BC作垂线,截取线段DG使得DG=DF,再作线段GF的垂直平分线,从而得到DE//BC;图(8)作BC的垂直平分线,再过点D作BC垂直平分线的垂线,从而得到DE//BC;图(9)以点D为圆心,DB为半径作圆,分别交AB,BC于点F,G,连接FG,过点D作FG的垂线,从而得到DE//BC,以上三种方法均利用在同一平面内垂直于同一直线的两条直线平行,从而由DE//BC得到∠ADE=∠B.
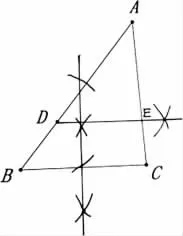
图(8)

图(9)
从以上图(7)、(8)、(9)的作图来看,对学生的逻辑推理能力要求更高了,“在同一平面内垂直于同一直线的两条直线平行”在平常的解题中我们经常用到,但是利用此定理来作图却很少,学生能归纳得出以上的方法,跨度和跳跃性都比较大,能够完成这样的作图归功于老师平常课堂的反复渗透,注重知识的整合与成网,注重学生逻辑推理能力的形成,正所谓:台上一分钟,台下十年功,只有老师平常注重逻辑推理的素养的形成才能收到以上的效果.
综上所述,初中数学课堂培养学生的核心素养体现了数学教育的意义与价值.学生数学素养的提高需要时间与积累,不积跬步无以至千里,我相信:只有不断地坚持,迎合学生的发展特点,充分了解核心素养的性质、内容及特征,将数学知识与核心素养相结合,以教材经典为母题,优化课堂设计,反复激活母题的内涵外延,注重直观抽象和数学模型的构建,注重分析对比和逻辑推理素养的提升,逐步积累,关注学生的成长特征,让学生真正感受到数学课堂的魅力,在潜移默化中促进学生形成良好的核心素养,是我们数学人的不断追求.

