抛体运动的难点探究
程彬 马仕彪
(安徽省濉溪中学)
抛体运动的规律很多,是曲线运动的基础,与很多运动都可以有机结合,在电场和复合场中都有广泛的应用.本文从抛体运动的基础入手,结合匀变速运动、牛顿第二定律等知识,对抛体运动的难点问题进行探究,并在广度和深度上进行延伸,以提高同学们的物理能力和学习兴趣.
1 平抛运动
1.1 两个重要推论
1)任意时刻瞬时速度的反向延长线一定通过这段时间内水平位移的中点,如图1所示,即
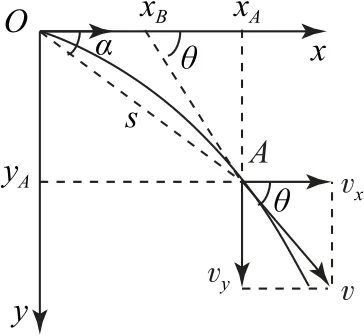
图1
2)任意时刻瞬时速度与水平方向夹角的正切值是位移与水平方向夹角的正切值的2倍,即tanθ=2tanα.
3)引申:a)如图2所示,从倾角为θ的斜面上将小球以速度v水平抛出,无论v多大,小球落到斜面上时与斜面夹角均相等;b)如图3所示,带电粒子以初速度v0垂直电场方向进入匀强电场,带电粒子在电场中做类平抛运动,在电场外观察粒子的出射情况,粒子“好像”是从电场中心射出的.

图2

图3
1.2 速度改变量
平抛运动的物体在任意相等时间间隔Δt内的速度改变量Δv=gΔt是相同的,方向恒为竖直向下,如图4所示.请注意,这里的速度变化量Δv为矢量.
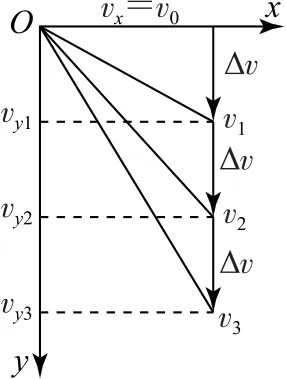
图4
1.3 约束条件下的平抛运动
对平抛运动考查的试题里,几乎所有情境都是有约束条件的.
1)影子的问题
对于抛体运动的影子问题,很多同学都容易出错,始终都不明白影子的运动情况,或者认为影子的运动就是小球的一个分运动.
如图5所示,点光源到竖直光屏的距离为d,紧贴点光源以速度v0水平向竖直光屏抛出一小球,小球在运动的过程中,会在光屏上留下一系列的影子.在t时刻,x=,由相似原理可知,化简得Y=·t,说明光屏上的影子做匀速直线运动.

图5
2)斜面上的平抛运动问题
a)从斜面抛出又落到斜面的时间.

图6
b)与斜面最远距离和经历的时间.
方法1 如图7所示,小球的速度方向平行于斜面时离斜面的距离最远,设经历的时间为t′,则vy=v0tanθ=gt′,故运动时间为,此时小球的水平位移为x′=v0t′=,小球速度方向的反向延长线交于处,故小球离斜面的最远距离

图7

方法2如图8 所示,把初速度v0、重力加速度g分别分解成沿斜面和垂直斜面的两个分量,即v0x=v0sinθ,ax=gcosθ.小球垂直斜面分速度为零时,经历时间

图8
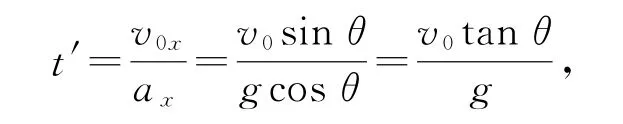
此时距离斜面最远,最远距离为
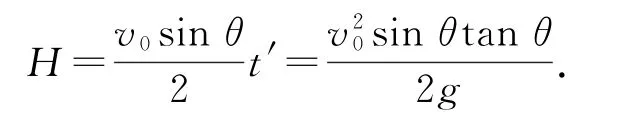
c)如图9 所示,斜面倾角为θ,从斜面上的某点分别以v1和v2(v1>v2)的速度水平抛出A、B两个小球,两小球在落点不发生反弹.
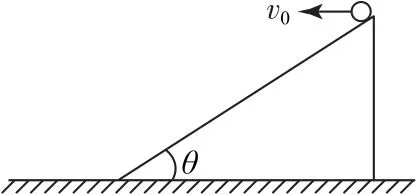
图9

3)半圆内的平抛运动问题
如图10 所示,由平抛运动知识和几何关系得h=,R±,可以得到以下结论.

图10
a)除h=R情况外,小球下落相同的高度时对应两个水平位移,因此v0可能有两解.
b)无论小球抛出的速度多大,都不可能垂直打在半圆上.
2 斜抛运动
2.1 抛出点和落地点高度相同的斜抛运动
如图11所示,物体以与地面夹角为θ、大小为v0的初速度从地面斜向上抛出,水平方向分速度vx=v0x=v0cosθ,竖直方向分速度vy=v0y-gt=v0sinθ-gt,由对称性知t上=t下=,上升的最大高度h=,水平射程
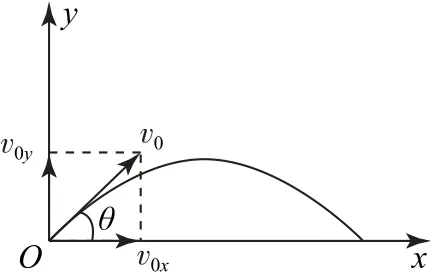
图11

2.2 抛出点和落地点高度不同的斜抛运动最大射程和最佳抛射角
很多同学可能会认为在任何情形下,当抛射角θ=45°时,水平射程都最大.形成这一错误认识的主要原因是学生所记的结论是从地面斜向上抛出的情形,而普遍的情况则是如图12所示的情形.

图12
方法1解析式法
在竖直方向上h=-v0sinθ·t+,水平方向上x=v0cosθ·t.两式结合可得
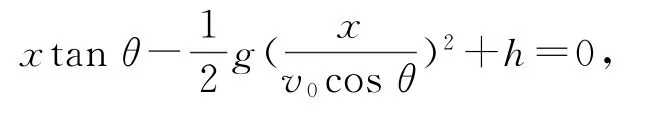
化简得


图13
2.3 斜面上的斜抛运动
如图14 所示,运动员从倾角为α的斜面上以与斜面的夹角为θ、大小为v0的初速度跳出,经过一段时间后,又落到斜面上.选择竖直向下为正方向,有y=-v0sin(θ-α)·t+gt2,vy=-v0sin(θ-α)+gt.水平方向上有x=v0cos(θ-α)·t,vx=v0cos(θ-α),y与x满足关系=tanα,设落到斜面时运动员速度与水平方向夹角为φ,tanφ==2tanα+tan(θ-α)为常量.
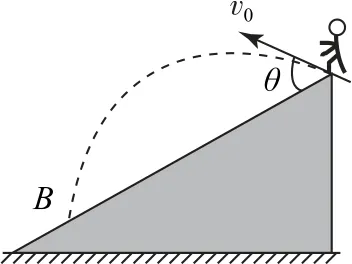
图14
3 抛体运动在生活、体育、军事等中的应用
3.1 雨伞甩水问题
如图15所示,雨伞边缘到伞柄距离为R,边缘高出地面高度为H,当雨伞以角速度ω绕伞柄匀速转动时,雨滴从伞边缘水平甩出而做平抛运动.设雨滴从伞的边缘以初速度v0沿切线做平抛运动,水平方向位移x=v0t,竖直方向位移H=,线速度与角速度满足的关系为v0=ωR,雨滴在地面形成圆的半径,结合以上各式解得r=.

图15
3.2 水管出水问题
如图16所示,一距地面高为h水平放置的水管,管内横截面积为S,水从管口处以速度v0源源不断地沿水平方向流出,假设水流在空中不散开,用t表示水由喷口到地面所用的时间,则有h=,水流稳定后在空中的体积为V=Sv0t=

图16
3.3 发球类问题
抛体运动在各类体育运动项目中很常见,下面以乒乓球的发球为例来说明.
例1如图17所示,已知一乒乓球台长为2L、网高为h,乒乓球与台面之间的碰撞为弹性碰撞,碰撞过程满足反射定律,不考虑乒乓球的旋转和空气阻力.重力加速度为g.

图17
(1)若球在球台边缘O点正上方高度为h1处以速度v1水平发出,落在球台上的P1点,如图17实线所示,求P1点距O点的距离x1;
(2)若球从O点正上方以速度v2水平发出,恰好在最高点时越过球网落在球台上的P2点,如图17虚线所示,求v2的大小;
(3)若球从O点正上方水平发出后,经反弹恰好越过球网且刚好落在对方球台边缘P3点,求发球点距O点的高度h3.

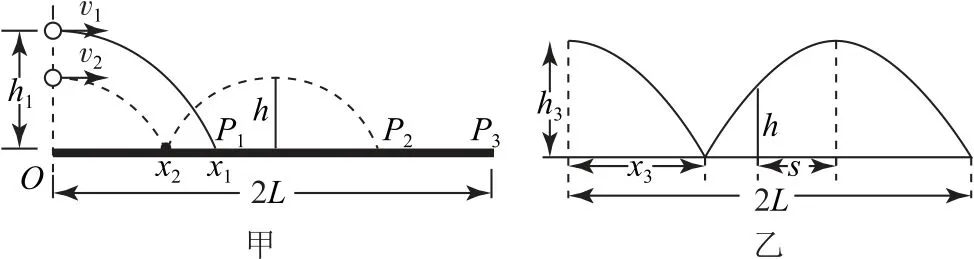
图18
点评本题综合性较强,“恰好越网”的临界点是这一题的关键,要求考生对乒乓球的发球规则有一定了解,并且要有扎实的几何知识才能将本题顺利解决.
3.4 射击问题
例2如图19所示,装甲车在水平地面上以速度v0=20m·s-1沿直线前进,车上机枪的枪管水平,距地面高h=1.8m.在车正前方竖直立一块高为2m的长方形靶,其底边与地面接触.枪口与靶距离为L时,机枪手正对靶射出第一发子弹,子弹相对枪口的初速度为v=800m·s-1.在子弹射出的同时,装甲车开始做匀减速运动,行进s=90 m 后停下.装甲车停下后,机枪手以相同方式射出第二发子弹.不计空气阻力,子弹可看成质点,重力加速度g取10m·s-2.
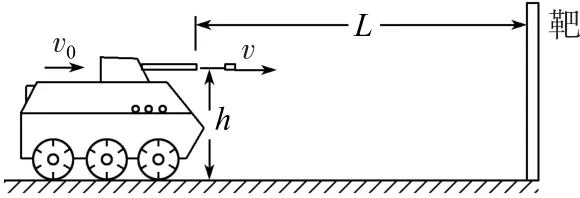
图19
(1)求装甲车做匀减速运动时的加速度大小;
(2)当L=410m 时,求第一发子弹的弹孔离地的高度,并计算靶上两个弹孔之间的距离;
(3)若靶上只有一个弹孔,求L的范围.

点评本题有两大难点,一是对“子弹相对于枪口的初速度为v=800m·s-1”的理解,并能将此速度转化为对地的速度;二是对“靶上只有一个弹孔”的理解,然后再找出对应临界值即可将问题解决.
4 抛体运动中的临界与极值
例3如图20所示,一轨道由半径为R=2m 的四分之一竖直圆弧轨道AB和长度可调的水平直轨道BC在B点平滑连接而成,现有一质量为0.2 kg的小球从A点无初速度释放,经过圆弧上B点时,传感器测得轨道所受压力大小为3.6N,小球经过BC段所受的阻力为其重力的0.2倍,然后从C点水平飞离轨道,落到水平地面上的P点,P、C两点间的高度差为3.2m,不计空气阻力,g取10m·s-2.
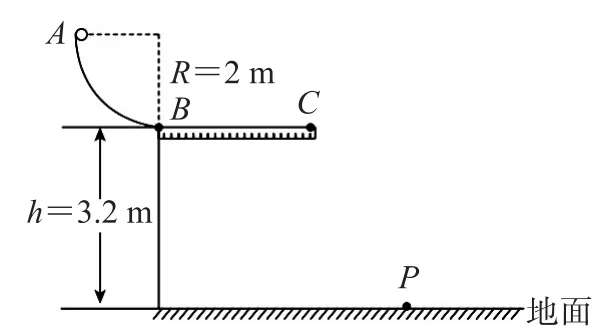
图20
(1)为使小球落点P与B点的水平距离最大,求BC段的长度和P与B点的水平距离的最大值;
(2)小球落到P点后弹起,与地面多次碰撞后静止,假设小球每次碰撞后机械能损失75%、碰撞前后速度方向与地面的夹角相等,求小球从C点飞出到最后静止所需的时间.

点评本题考查的数学知识较多,但物理与数学还是有很大差异的,问题的本质还应该落在物理上,而不是纯粹的数学计算,否则将失去物理应有的本性.
5 抛体运动与其他运动的结合
例4如图21所示,长为R=0.4m 的轻绳一端固定在O点,另一端系一质量为m=0.5kg的小球,现将绳子拉成竖直状态,小球处于最高点.现给小球一个大小为v=m·s-1的水平初速度,g取10m·s-2.求小球运动到最低点时轻绳的拉力.
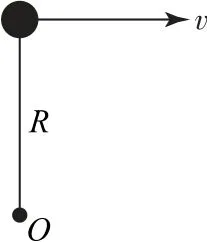
图21
解析如果小球恰好能做完整的圆周运动,在最高点mg=,代入数值得v0=2m·s-1,所以当v≥2m·s-1时小球才能做完整的圆周运动.
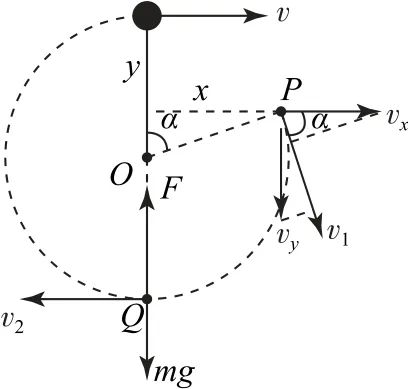
图22
设绳子绷紧瞬间OP与竖直方向夹角为α,此过程x=vt,y=,结合这几个关系式,可以解得α=60°,t=0.2s,vy=gt=2m·s-1.
绳子绷紧后瞬间,速度会出现突变,即沿绳方向上的速度突变为零,只剩下沿垂直于绳方向上的速度,机械能有损失.因此只要将P点分速度vx和vy沿绳的方向与垂直于绳的方向进行分解,然后再合成就可以了,即v1=vxcosα+vysinα=m·s-1,从绳子绷紧到最低点应用动能定理有mgR(1+cosα)=,在最低点应用向心力公式有F-mg=,解得F=28.4375N.
点评在绳子绷紧的瞬间,速度出现了突变,导致动能瞬间减小.很多考生在解决本题时,可能没有考虑到这一点而造成错误.
抛体运动可考查的范围很广,难点很多,但只要掌握了抛体运动的基本知识和规律,有关抛体运动的问题便可迎刃而解.
(完)

