基于有限数据的线性系统重构与采样控制
张智豪, 楼旭阳
(江南大学物联网工程学院, 江苏 无锡 214122)
近年来, 线性系统的控制问题受到专家学者们的广泛关注. 当系统被控对象无法准确建模时, 基于模型的控制方法面临极大挑战, 甚至无法设计出有效的基于模型的控制器. 数据驱动理论可以利用被控系统的输入输出数据进行重构系统, 由此摆脱对被控对象模型的依赖, 提高了控制系统的鲁棒性, 并能够有效处理被控对象难以建模的控制问题[1]. 然而, 目前基于离线数据驱动的学习算法,如最大似然法[2]、预测误差法[3]以及子空间法[4]等, 要求输入输出数据量较为庞大致使其应用范围受限, 或须对观测数据进行分组而导致重构精度下降[5-6]. 基于有限数据的系统重构方法[7]具有较大潜力, 相较于最大似然法和预测误差法, 其操作简单且在输入充分激励的条件下能较好地实现系统重构.
由于连续状态反馈控制对系统的实时性要求较高, 故离散时间的反馈控制备受关注. 作为一种离散时间的反馈控制策略, 采样控制不仅能提高系统的控制精度和抗干扰能力, 而且可提升控制器的利用率和通用性. 由于采样控制只在数据采样时更新控制信号,故与传统的连续控制相比, 其信息传输量低且控制效率高[8]. 输入时滞方法[9]是一种处理采样控制的有效方法, 其核心思想是通过带有时滞的控制输入来建立采样系统模型,并建立具有线性矩阵不等式(linear matrix inequality, LMI)形式的稳定性准则[10]. 与现有其他方法相比,输入时滞法简单方便且应用范围更广泛. 任涛等[11]利用输入时滞法将含有采样同步控制器的混杂系统转换为具有输入时滞的连续系统,并给出了使误差系统稳定的充分条件,确保混沌系统在所容许的扰动下实现完全同步; Zeng等[12]在研究混沌Lur’e系统的采样数据同步问题时改进了现有的输入时滞法, 首次提出输入时滞相关自由矩阵零等式方法, 并通过构造全新的Lyapunov泛函得到LMI形式的同步准则, 降低了现有结论的保守性. 本文拟基于有限数据策略对一类系统矩阵未知的线性系统进行重构,并采用输入时滞法对重构后的系统进行闭环采样控制,以期实现闭环系统稳定性.
本文中,Rn为n维欧几里得空间,Rn×m为n×m维实矩阵空间,In为n维单位矩阵, diag{…}表示对角矩阵, *表示对称矩阵块中相应位置的转置, †表示矩阵的右逆,X≥Y表示X-Y是半正定的, 其中X和Y是同维矩阵.
1 系统重构
考虑如下连续线性系统:

(1)
其中系统状态z∈Rn, 参数A∈Rn×n,B∈Rn×m未知, 控制输入u∈Rm.
采用欧拉离散化方法对连续系统(1)进行离散化处理,即
(2)
其中k为正整数,α为步长.
将连续系统方程(1)代入式(2), 得
(3)
当步长α充分小时, 有
(4)
此时, 系统(1)的离散化形式为
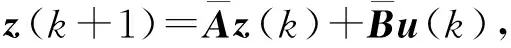
(5)
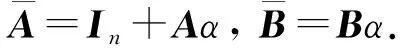
引理1[7]若系统(5)满足秩条件
(6)
则系统(5)等价于
(7)
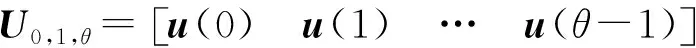
注1为了满足输入充分激励的条件, 对输入序列长度θ的唯一要求是θ≥(m+1)n+m.若满足该条件, 引理1中条件(6)即成立.这是由于条件(6)与输入充分激励的条件等价.在满足条件(6)的前提下, 输入序列θ越长, 获得原系统的信息会越多, 从而系统重构的精度越高.
注2注意到
(8)
由此可得
(9)
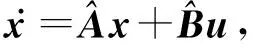
(10)
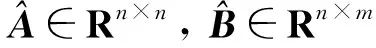
2 采样控制
利用输入时滞方式对重构后的线性连续系统(10)进行采样控制.采样控制器中反馈数据来自重构后的系统(10).当离散化步长α充分小时, 即重构精度足够小,反馈数据将充分接近原系统数据.
由于重构后的系统是开环的, 故须通过设计采样控制器构成闭环系统.设计采样控制器
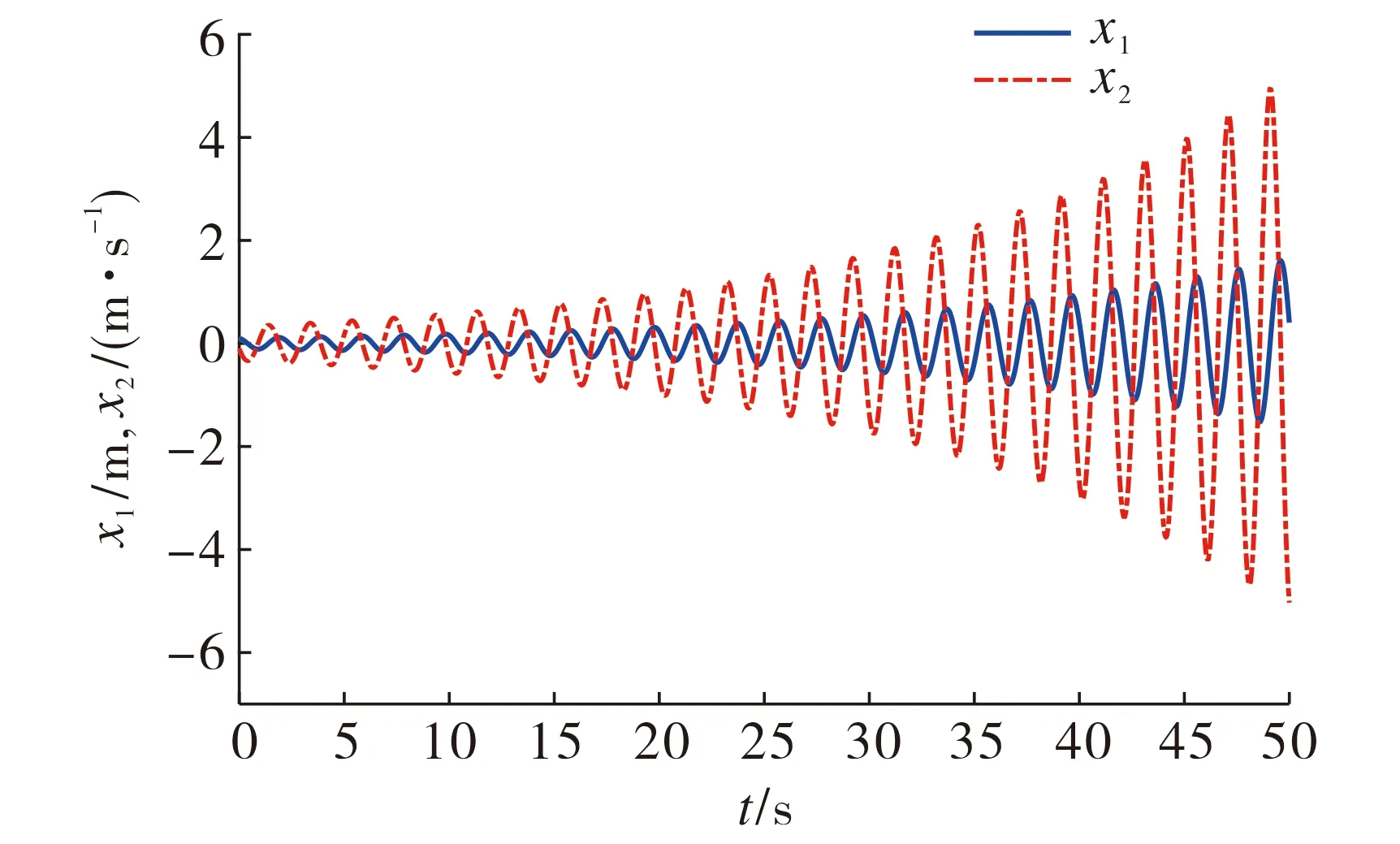
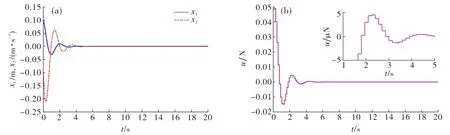
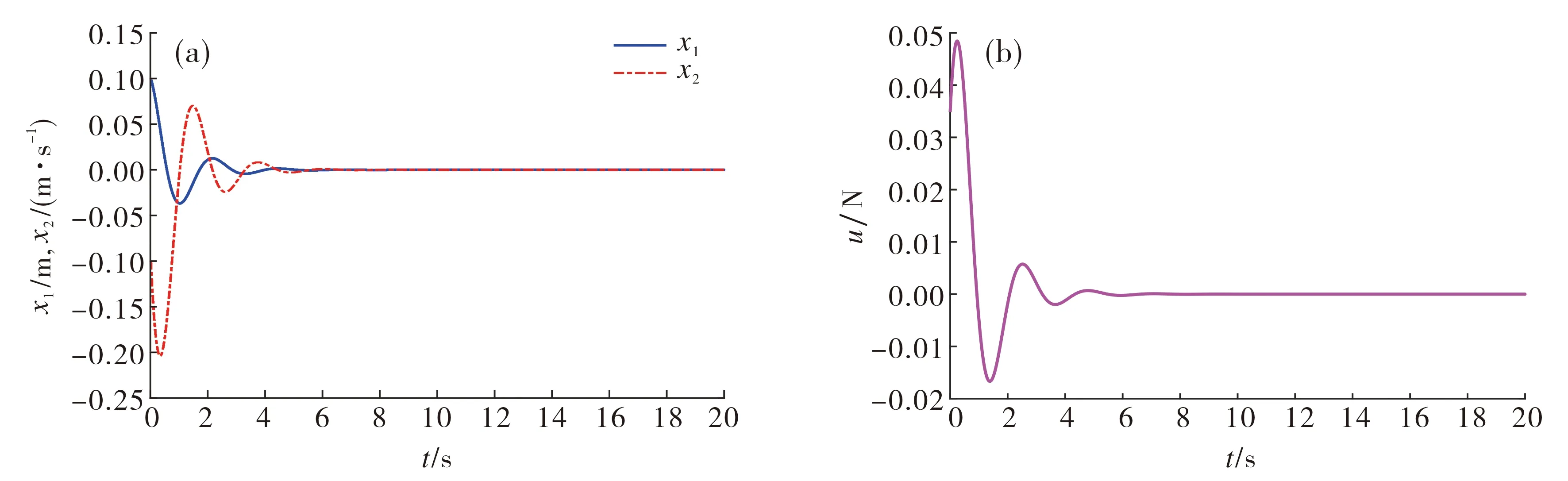
u(t)=Kx(tk),tk≤t (11) 其中K∈Rm×n为待设计的控制器增益,x(tk)为采样数据, 采样时刻tk满足如下条件: 0=t0 Δk=tk+1-tk≤h, ∀k≥0, 其中Δk为采样时刻tk和tk+1间的时间间隔,h为最大采样周期. u(t)=Kx(t-τ(t)),∀t≥0. (12) 进而得到系统(10)的闭环连续系统 (13) 引理2[13](Jensen不等式) 对于任意的对称正定实矩阵M∈Rm×m, 常数δ>0以及向量值函数ω:[0,γ]→Rm, 有 (14) (15) 定理1对于时滞系统(13), 给定增益矩阵K和最大采样周期h>0.如果存在对称矩阵P>0,Q>0,R>0以及矩阵X11,X12,X22,Y,U,满足下列不等式: (16) (17) 证明 考虑Lyapunov泛函 (18) 沿闭环系统(13)的状态轨迹对时间t求导, 可得 (19) (20) 将式(20)代入式(19), 得 (21) (22) 将式(22)代入式(21),可得 (23) (24) 若令Lyapunov泛函(18)中的R=0, 则易得到下面的推论. 推论1对于时滞系统(13), 给定增益矩阵K和最大采样周期h>0.如果存在对称矩阵P>0,Q>0以及矩阵X11,X12,X22,Y,U,满足下列不等式: (25) (26) (27) (28) (29) (30) 注4事实上, 定理2是在定理1的基础上发展而来的,同时定理2给出了采样控制器参数的设计方法.因而, 由定理2中线性矩阵不等式求解得到的控制器可以使得闭环系统渐近稳定,即定理2是定理1的充分条件. 考虑质量-弹簧-阻尼系统 图1 无控制输入时系统状态x1和x2 的时间响应曲线Fig.1 Time responses of states x1 and x2 without control input 对系统采用采样反馈控制律(12), 采样周期为0.15 s时系统状态x1和x2及控制器u的时间响应曲线如图2所示.由图2可见: 在基于有限数据重构系统矩阵设计的采样控制作用下, 系统状态渐近稳定; 控制器u每过一个采样周期才更新一次控制信号. 图2 采样周期为0.15 s时系统状态x1,x2(a)及控制器u (b)的时间响应曲线Fig.2 Time response of states x1 and x2 (a), and control input u (b) when the sampling period is 0.15 s 为了体现采样控制器的优越性, 采用相同的状态反馈控制形式对系统进行连续控制,得到系统状态x1和x2及控制器u的时间响应曲线如图3所示. 图3 连续控制时系统状态x1,x2(a)及控制器u (b)的时间响应曲线Fig.3 Time response of states x1 and x2 (a), and control input u (b) in continuous control 对比图2和图3可知: 采样控制与连续控制下的系统状态差异较小; 采样控制只在数据采样时刻更新控制信号的特点使得信息的传输量大幅减少, 控制效率得到很大提升. 本文考虑一类参数矩阵未知的连续线性系统,通过有限数据策略对系统矩阵进行重构并实现了对重构系统的采样控制. 该重构方法操作简单易行,重构精度高,通过有限的输入输出数据即可计算得到系统矩阵. 通过输入时滞法实现的采样控制方案可以建立线性矩阵不等式形式的稳定性准则,继而根据Lyapunov理论进行验证分析. 相较于连续控制,采样控制方法减少了信息的传输量,提高了闭环系统的控制效率. 今后将进一步推广基于数据驱动方法处理双线性系统或Lipschitz非线性系统的重构和控制问题.
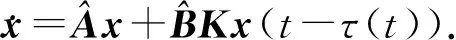
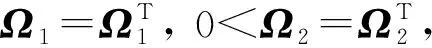
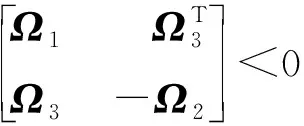
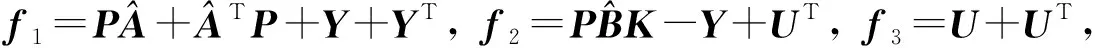
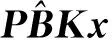
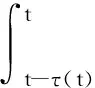
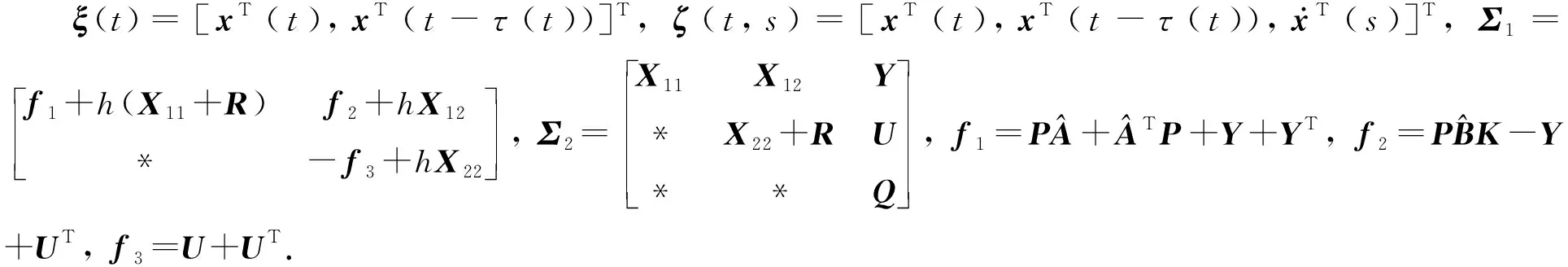
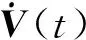
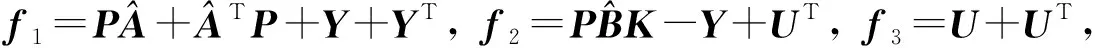
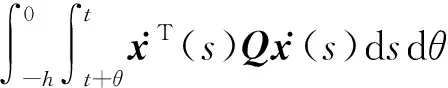

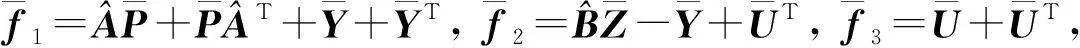
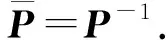
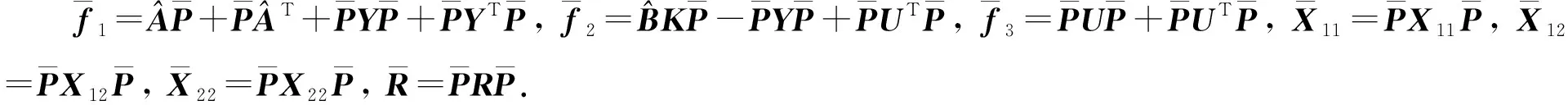
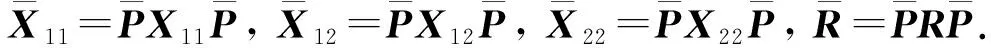
3 仿真实例
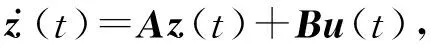
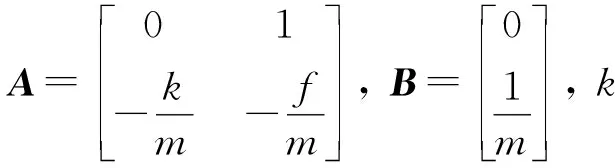
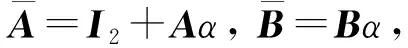
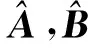
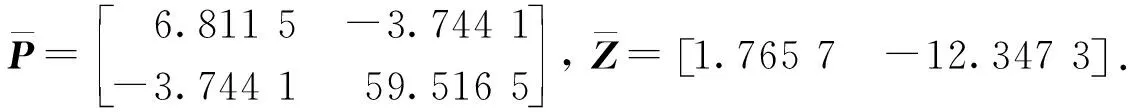
4 结语

