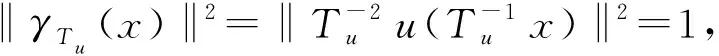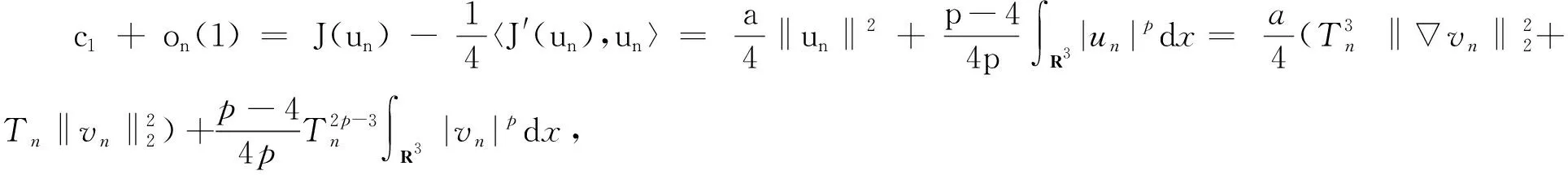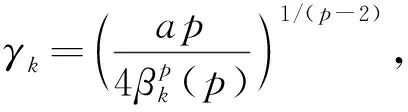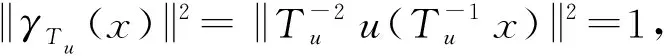R3中一类Kirchhoff-Schrödinger-Poisson系统的高能量径向解的存在性
杨金富, 张家锋
(贵州民族大学数据科学与信息工程学院, 贵阳 550025)
Kirchhoff-Schrödinger-Poisson系统的一般形式为
(1)
该系统有很强的物理学背景,许多研究者对该类系统的正解和多解进行了大量的研究,取得了丰富的结果.Li等[1]在非线性项f(x,u)是一般奇异项的假设下, 得到了系统(1)解的存在唯一性; Lü[2]考虑了具有一般非线性项的系统, 通过对非线性项f的限制, 利用单调性方法和截断技术, 得到了系统(1)正径向解的存在性; Zhang[3]研究了一类带有奇异项的系统(1), 通过变分法与Nehari流形相结合的方法, 得到该类系统正解的存在性、唯一性以及多重性结果.
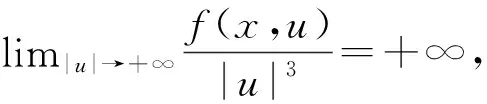
1 主要成果
考虑Kirchhoff-Schrödinger-Poisson系统
(2)
其中a>0,b>0, 4.5 定理1假设a>0,b>0,4.5 注2本文给出含有纯幂次非线性项f(x,u)=|u|p-2u(4.5 嵌入H1(R3)Lp(R3) (2 引理3对于任意u∈H1(R3), 有 i) 任意u∈H1(R3),φu≥0, 且‖φu‖D1,2(R3)≤C1‖u‖2(∃C1>0); ii)φtu=t2φu, ∀t>0, ∀u∈H1(R3); iii) 若在H中有un⇀u, 则D1,2(R3)中就有φun⇀φu,且 v) 如果u(x)是径向函数, 则φu也是径向函数. 利用变分法可将问题(2)等价转化为I(u)=minu∈HJ(u) (φu∈D1,2(R3)), 其中 (3) 且J(u)关于任意v∈H的弱导数为 (4) 命题4(喷泉定理)[15]设X是一个无限维巴拿赫空间,φ∈C1(X,R)并满足(PS)c条件, 且φ(-u)=φ(u) (∀u∈X), 若∀k∈N, ∃ρk>γk>0, 有: i)bk=infu∈Zk,‖u‖=γkφ(u)→+∞(k→+∞); ii)ak=maxu∈Yk,‖u‖=ρkφ(u)≤0, 则φ(u)存在一个临界序列{uk}, 使得φ(uk)→+∞(k→+∞). 受文献[11,13]的启发, 对于任意u∈H{0}, 可先考虑这样一条路径,设 γt(x)=t-2u(t-1x),t>0, (5) 则 (6) 且 (7) 由式(6)知, limt→0+‖γt(x)‖2=+∞且limt→+∞‖γt(x)‖2=0, 故对于任意u∈H{0}, 存在唯一的Tu>0, 使得 (8) 此外, 当‖u‖→+∞时,‖Tu‖→+∞.由式(5)知, 对于任意u∈H, 都有唯一的t-2u(t-1x)与之对应, 则可以做一个一对一的函数FTu:H→S, (9) 且 (10) 其中S={u∈H:‖u‖=1}是一个单位球面. 引理5J(u)关于u是偶的. 证明 由式(3)知J(0)=0, 且 故J(u)关于u是偶的. 引理6对于任意c∈R,J(u)满足(PS)c条件. 证明 设序列{un}⊂H使得 J(un)→c,J′(un)→0. (11) 由式(3)和(4)知 两式相减, 得 (12) 由于a>0, 4.5 limn→+∞(c1+on(1))=c1, (13) (14) 有c1=+∞, 显然矛盾,故假设不成立.因此,序列un在H中是有界的, 有 (15) (16) 引理7J(u)满足命题4中条件(i), 即设a>0,b>0,4.5 bk=infu∈Zk,‖u‖=γkφ(u)→+∞(k→+∞). 证明 由文献[7]中引理2.5知, 当2 βk(p)=supu∈Zk,‖u‖=1‖u‖p→0(k→+∞), (17) (18) 即存在γk>0, 使bk=infu∈Zk,‖u‖=γkJ(u)→+∞ (k→+∞). 引理8J(u)满足命题4中条件(ii), 即设a>0,b>0,4.5 则由实数的稠密性可知, 存在‖uk‖∈R有-∞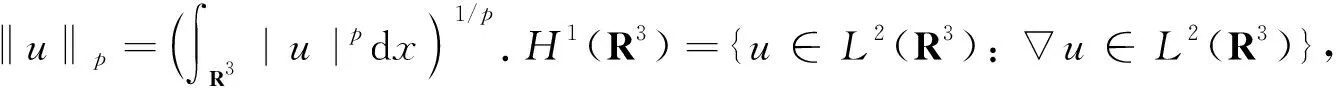

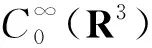
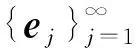
2 定理1的证明