输入非线性系统的多步长搜索梯度迭代算法
程连元, 荣英佼, 黄文军, 李珊珊, 陈 晶*
(1. 江南大学理学院, 江苏 无锡 214122; 2. 中国人民解放军63983部队, 江苏 无锡 214028;3. 近地面探测技术国防重点实验室, 江苏 无锡 214028)
在网络控制系统中,输入信号通过网络传输到执行器, 由于网络的不确定性和信号间的转换特性, 执行器的输入信号通常具有非线性特性.输入非线性系统广泛存在于工业过程的各个领域[1-3],其辨识研究有着重要的理论意义和实用价值[4-5].系统辨识方法主要分为两类:一类是离线算法,即一次性采集所有输入和输出数据,利用数据反复迭代实现参数更新[6-7];另一类是在线算法,即随时采集数据并利用即时数据更新参数[8-9].离线算法速度更快、精度更高,如最小二乘算法(least squares,LS)、梯度迭代算法(gradient iterative,GI)等.LS算法须求解矩阵的逆,计算量较大,故不适用于大规模系统辨识. GI算法的基本思想是以一个随机选择的参数估计值为初始值,每次选择一个合适的方向(负梯度)和合适的步长对当前估计值进行更新, 故方向和步长是优化GI算法的两大设计要素.通过改变步长可以提高收敛速度,如最速下降法[10]、投影算法[11]、带遗忘因子的梯度法[12]等,但以上方法都须求解矩阵的特征值,当矩阵阶数即系统维数较大时,矩阵的特征值求解非常具有挑战性.针对如何在确定迭代最优步长时避免求解矩阵特征值的问题,本文借鉴粒子群算法思想[13],首次提出多步长搜索梯度算法.在每次迭代过程中随机产生若干步长,再由构造的代价函数选择每一步中的合适步长,根据该步长更新系统参数.与传统的梯度算法相比,本文方法的收敛速度更快,辨识效率更高,适用于大规模和丢失数据的系统辨识.
1 问题描述
设输入非线性系统t时刻的输出y(t)=a1y(t-1)+…+amy(t-m)+b1f1(U(t-1))+…+bnfn(U(t-1))+v(t), 其中fi(U(t-1))是关于自变量U(t-1)的非线性函数, 且结构已知;U(t-1)={u(t-1),…,u(1)}, 式中u(t)代表系统t时刻的输入;v(t)是t时刻服从未知高斯分布N(0,σ2)的噪声.本文主要目的是利用可测的输入信号u(t)和输出信号y(t)对未知参数ai(i=1,…,m)和bj(j=1,…,n)进行辨识, 模型的阶数n和m已知.为方便辨识, 将上述模型整理为自回归形式
收集L组输入输出数据, 并定义Y(L)=[y(L),…,y(1)]T∈RL,U(L)=[u(L),…,u(1)]T∈RL,Φ(L)=[φ(L),…,φ(1)]T∈RL×(m+n),V(L)=[v(L),…,v(1)]T∈RL, 则输入非线性模型可转化为Y(L)=Φ(L)θ+V(L).
2 多步长梯度迭代算法
GI算法是一种常用的迭代优化算法, 在获得完全的数据集后,通过寻找每一次迭代的方向及步长可以逐步逼近所辨识的参数[14-15].本文利用GI算法对输入非线性系统进行辨识.参数第k次的估计值θk=θk-1+γk-1[Y(L)-Φ(L)θk-1], 其中步长γk-1须满足条件0<γk-1<2/λmax, 式中λmax是矩阵[ΦT(L)Φ(L)]的最大特征值.由于[ΦT(L)Φ(L)]∈RP×P,P=m+n, 故当P值很大时, 在传统GI算法中求解矩阵特征值非常困难.本文通过建立群体搜索当前迭代中较优的迭代步长并结合迭代方向更新参数估计值, 即每一步迭代过程中随机产生多个步长, 根据迭代函数找出当前最优步长,进而避免了求解矩阵特征值的运算.




图1 算法流程图Fig.1 Flowchart of the M-GI algorithm
3 在具有丢失数据非线性系统中的应用
传统GI算法中, 当输入和输出数据均可测时, 信息矩阵Φ(L)不会随着迭代次数的变化而变化, 即矩阵ΦT(L)Φ(L)的特征值不变, 在第一次迭代时就可计算出其特征值, 并选择合适的步长保持不变, 故其计算量主要在第一次计算特征值时产生.
4 模拟仿真
利用MATLAB仿真平台对如下非线性系统进行仿真研究:

图2 系统噪声、输入以及输出数据Fig.2 System noise, input and output data
输入数据{u(t)}采用服从高斯分布N(0,1)的可测随机序列,{v(t)}采用服从N(0,0.12)的高斯白噪声序列, 步长数量s=8.非线性系统的噪声、输入数据、输出数据如图2所示.
分别使用GI算法和多步长搜索GI算法对非线性模型进行参数辨识, 其中多步长GI算法根据不同的步长范围d分为两种: 设d=2/λmax时, 算法命名为M-GI-1; 设d=10/λmax时, 算法命名为M-GI-2.不同算法的参数误差τ=‖θk-θ‖/‖θ‖随迭代次数变化的曲线如图3所示.图3说明, 与传统GI方法相比, 多步长搜索GI方法对系统参数的辨识速度更快, 效率更高.M-GI-2算法比M-GI-1算法更稳定, 说明多步长搜索GI方法中上限值的选择更合适.图4为M-GI-1和M-GI-2算法的步长随迭代次数的变化曲线.图4显示, 当步长范围上限较大时, M-GI-2方法每次迭代的步长变化较大, 表明其选择范围较大, 故其收敛速度高于M-GI-1方法(见图3).
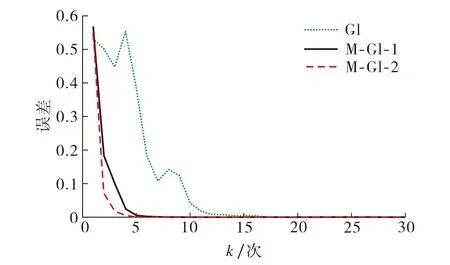
图3 参数误差随迭代次数变化曲线Fig.3 Curve of variation of parameter error with iteration number
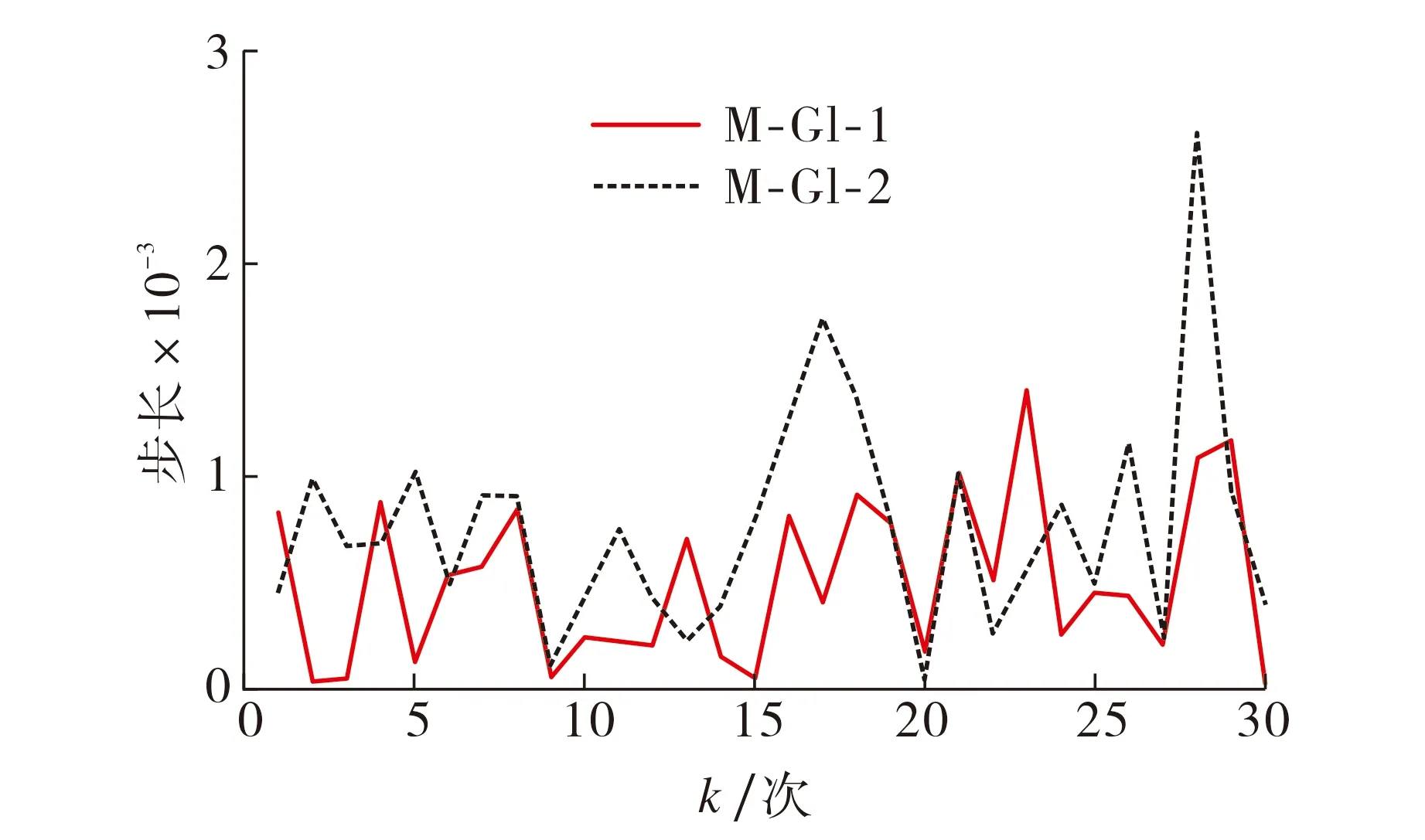
图4 多步长M-GI算法每次迭代的步长Fig.4 The step-length of the M-GI algorithm
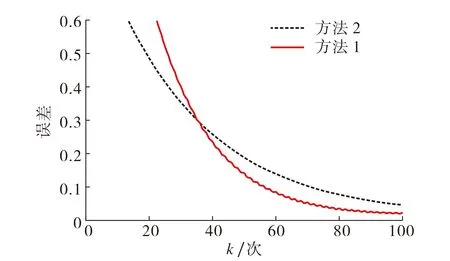
图5 两种方法的参数误差图Fig.5 Parameter estimation errors using the two methods
图5为采用两种不同的参数估计值求解方法(即不同的权值选择方法)对系统进行辨识的参数误差.图5显示, 方法1和方法2均能使参数达到收敛,但方法1仅考虑一个值对参数估计的影响,因此在初始阶段的收敛效果一般,但当参数接近真值时,其收敛速度快速提高.因此建议在初始阶段使用方法1,在后续阶段使用方法2.
5 结论
本文针对输入非线性系统提出了一种多步长搜索梯度迭代方法,该方法在每一次迭代过程中随机产生多个步长,避免了求解高阶矩阵特征值的问题,更适合大规模系统的参数辨识.仿真结果表明,本文方法收敛速度快,当系统存在数据丢失情况时,该方法的计算量相比于传统GI方法明显减少.该算法在深度学习和机器学习中具有广泛的应用前景,同时,其收敛性的理论证明以及步长范围的上限选择仍有待进一步研究.

