分数阶超混沌Chen系统的RBF神经网络自适应滑模同步

邵克勇, 冯 奥, 王婷婷

(东北石油大学电气信息工程学院, 黑龙江 大庆 163318)

分数阶微积分被广泛应用于物理学和工程学[1]．随着科技的进步,分数阶微分理论已被用于信号分析与加密处理[2]、非牛顿流体力学[3]和系统动力学控制[4]等领域．近年来, 分数阶超混沌系统的同步控制研究备受关注．目前,已有的同步控制方法有自适应神经网络控制[5]、滑模控制[6]和干扰观测器控制[7]等．邓立为等[8]以一类分数阶超混沌系统为同步研究对象, 设计了一种基于输出反馈的滑模控制器,为分数阶超混沌系统的同步研究提供了新的思路; Ni等[9]针对分数阶超混沌Liu系统设计了一种固定时间滑模控制器,该方案下2个分数阶超混沌Liu系统在固定时间内完成同步; Sun[10]针对一类非同阶分数阶超混沌系统的同步,设计出一种含自适应参数的滑模控制器, 实现了该系统的完全同步;本课题组在前期工作[11]中利用径向基函数(radial basis function, RBF)神经网络逼近不确定项, 通过自行设计的自适应神经网络控制器对不确定项或外部干扰进行补偿控制, 解决了分数阶不确定性系统的同步控制问题; Wang等[12]设计了一种时间调节有限的新型滑模控制器, 该控制方案下滑模面可在有限时间内收敛至零, 进而实现分数阶超混沌系统的有限时间同步, 并将该方案应用于分数阶超混沌金融模型的控制, 得到良好的控制效果．本文拟设计一种RBF神经网络自适应滑模控制器, 以期实现分数阶超混沌Chen系统的同步．

1 问题描述

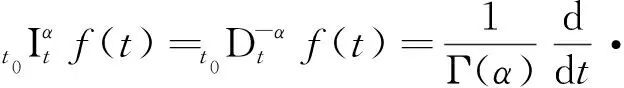
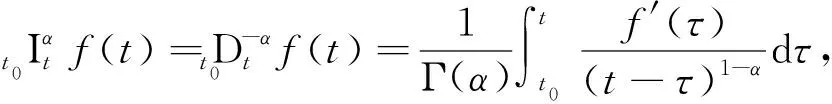
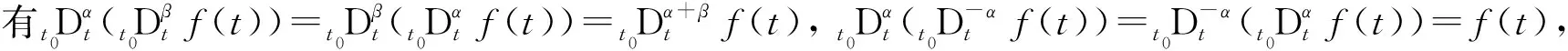
定义n维分数阶超混沌系统的驱动系统

Dαx=Ax+f(x),

(1)

其中0<α<1; 系统的状态向量x∈Rn;A∈Rn×n,f(x)∈Rn分别为驱动系统的线性和非线性部分．其响应系统

Dαy=By+g(y)+d+u,

(2)

其中0<α<1; 系统的状态向量y∈Rn;B∈Rn,g(y)∈Rn分别为响应系统的线性和非线性部分;d∈Rn为外部扰动;u∈Rn为控制器输出．

定义系统误差

e=y-x．

(3)

将式(1)(2)代入式(3), 可得如下误差系统:

Dαe=By-Ax+g(y)-f(x)+d+u．

(4)

驱动系统与响应系统欲实现同步, 须通过控制律使得误差e收敛至零, 即limt→∞‖e‖=limt→∞‖y-x‖=0．

引理1[14]考虑分数阶系统Dαx(t)=Cx(t), 其中0<α<1,x(t)为系统的状态向量,C为系统的参数矩阵．

当0<α<1时, 若系统参数矩阵C的所有特征值都小于等于零, 则该系统是渐近稳定的．

2 RBF神经网络和滑模控制器设计

2.1 RBF神经网络

现采用RBF神经网络对外部干扰d进行自适应逼近, 以降低外部干扰对控制器切换增益的影响．假设

d=W*ΤH+ε,

(5)

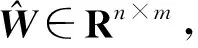
2.2 滑模控制器设计

选取滑模面

(6)

当系统发生滑模运动时,系统状态沿滑模面前进, 此时有

(7)

(8)

由式(8)可得

(9)

由引理1可知式(8)是渐近稳定的且滑模面对干扰不敏感, 故系统具有较好的鲁棒性．

对误差系统(4)设计控制律:

(10)

自适应律:

(11)

(12)

式中自适应律的调节参数λ>0,γ>0; 系统滑模面向量s∈Rn; 自适应系数k∈R．

定理1在控制律(10)及自适应律(11)(12)的作用下,误差系统(4)趋于稳定,响应系统与驱动系统能够实现同步．

证明 将式(5)(10)代入误差系统(4),得

(13)

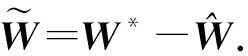
由Lyapunov稳定性定理可知limt→∞e=0, 故误差系统(4)在控制律(10)及自适应律(11)(12)的作用下趋于稳定, 上述控制方案用于分数阶超混沌Chen系统的同步是可行的．

3 数值仿真

为了验证本文方法的有效性, 运用MATLAB 2018b对分数阶超混沌Chen系统进行数值仿真．

考虑分数阶超混沌Chen系统的驱动系统状态方程

(14)

响应系统为

(15)

当α=0.9时, 系统(14)的超混沌吸引子如图1所示．由图1可知,该系统具有超混沌特性．

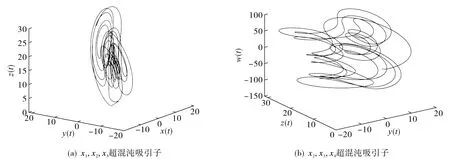
图1 分数阶超混沌吸引子Fig.1 Fractional-order hyperchaotic attractor

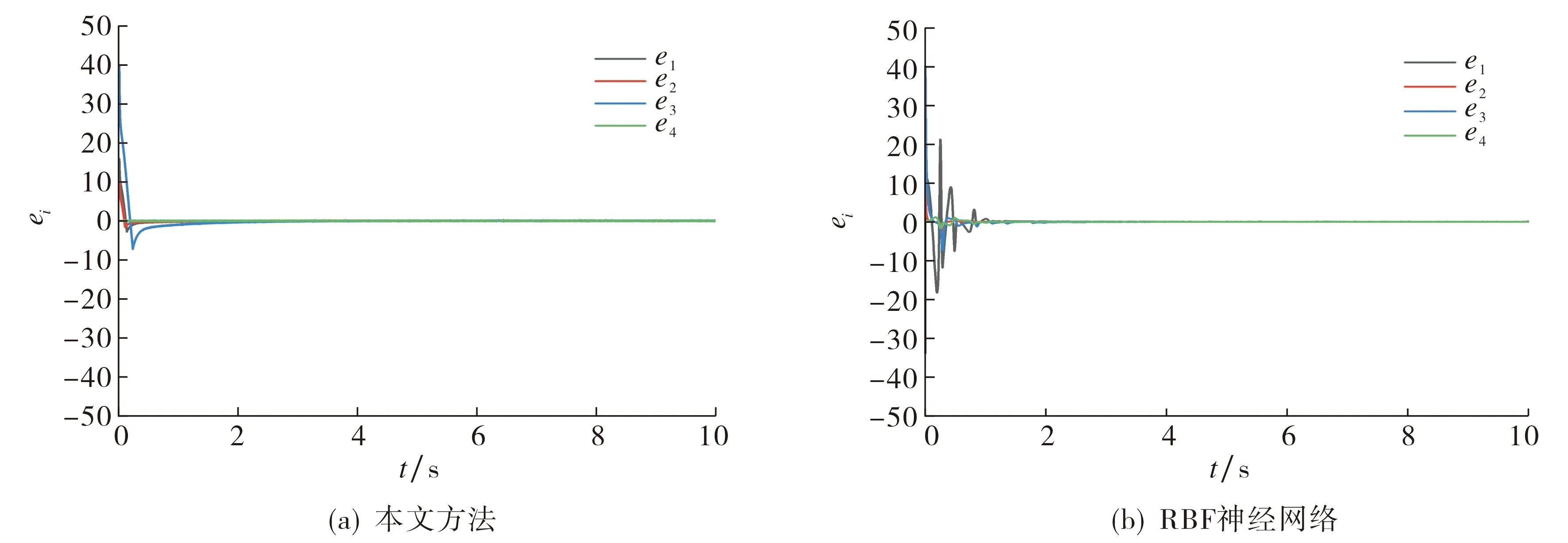
图2 无外部干扰时的同步误差曲线Fig.2 Synchronization error curve without external disturbance

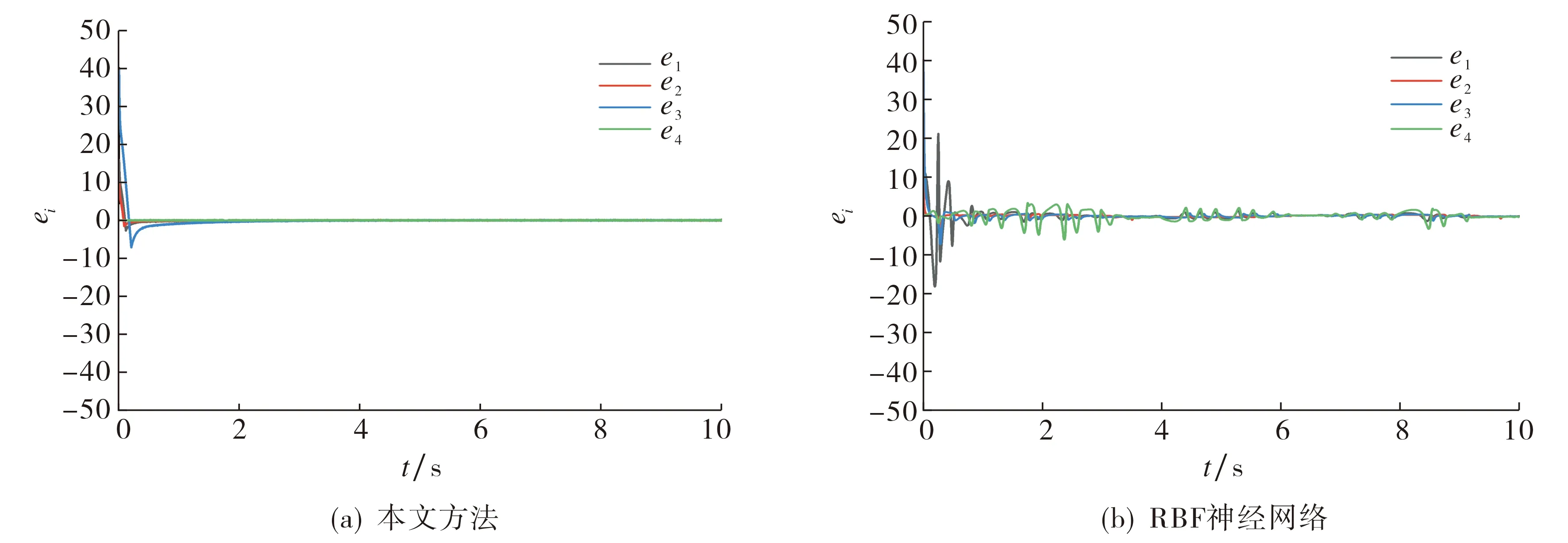
图3 外部干扰下的同步误差曲线Fig.3 Synchronization error curve with external disturbance

由图2～3可见, 与RBF神经网络控制方案[11]相比, 本文方案的控制精度更高, 同步误差收敛速度快, 所需调节时间短,控制效果更佳; 自适应滑模控制器的引入使得系统具有较高的鲁棒性, 在出现较强外部干扰时其控制性能仍保持不变．

4 结论

本文通过构建合适的分数阶超混沌Chen系统分数阶滑模面,在滑模控制理论的基础上增设自适应参数,并利用RBF神经网络逼近外部干扰后进行补偿,抑制可能出现的外部干扰对控制器切换增益的影响,从而实现系统的同步控制．运用Lyapunov原理对所设计方案的可行性进行理论推导与分析,并提供数值仿真验证了方案的有效性．本文方案从理论上能有效减少滑模控制所致抖振,并能抑制较强外部干扰对系统控制质量的影响和提高系统鲁棒性．在实际应用中可降低控制器负荷和控制成本,使理论联系实际成为可能,为分数阶超混沌系统的同步研究提供了新思路．然而,本文方案未彻底消除滑模控制器的抖振,其可能原因是切换增益的自适应律恒为正数,导致切换增益不断变大,进而产生抖振．今后将尝试采用粒子群或差分进化等优化算法对切换增益进行优化,使得切换增益恒定,从而进一步减少甚至消除抖振．