基于参数优化动态GPR的反应釜出料浓度预测

覃溢波, 柳天虹, 任春雨, 齐胜利

(扬州大学信息工程学院, 江苏 扬州 225127)

连续搅拌釜式反应器(continuous stirred tank reactor, CSTR)是化工生产过程中进行各种物理变化和化学反应广泛使用的设备, 在反应装置中占有重要地位．釜内搅拌装置的主要作用是使反应釜内物料混合均匀且物料温度处处相等,以保证物料的质量和反应釜的安全性．近年来, 关于CSTR的研究主要集中在反应釜预测控制[1-2]及状态估计[3]等方面．由于釜式反应器中化学反应机理较复杂,所采集的数据通常表现出非线性强、样本维数高以及存在较大噪声和孤立点等特性．目前,针对反应釜输出量的预测主要采用神经网络模型[4-5],该模型以经验风险最小化为原则,模型建立在样本数趋于无穷的基础上, 但是实际训练样本往往是有限的, 导致训练过程中模型过于复杂而产生过拟合现象．高斯过程回归(Gaussian process regression, GPR)[6]因结构灵活性高而成为主流的机器学习模型之一．GPR是一种非参数建模方法, 可表征为随机变量的集合, 其中的任意随机变量组合均服从联合高斯分布．GPR也可等效为一种特殊结构的神经网络, 即隐含层含有无限节点的神经网络．相较于神经网络等方法, GPR因包含的参数较少, 故参数优化过程简单且更易收敛,建模时可将先验知识表征为先验概率融入模型,通过选取不同类型的协方差函数增强模型对实际过程的解释能力．GPR被广泛用于锂电池功率预测和健康状态估计[7-8]、风电功率预测[9]、柴油机氮氧化物预测[10]以及大型核动力涡轮发电机的涡流损耗预测[11]等领域．在已有的研究中, 模型多为静态非线性映射模型,即基于过程处于稳定工况的假设．然而, 工业过程中存在多种动态特性, 故有必要建立动态GPR模型, 不仅考虑当前输入对输出的影响, 而且须考虑过去的输入和输出对系统当前输出是否产生影响．GPR模型的精度取决于协方差函数中参数的优化程度．通常采用共轭梯度算法优化GPR模型参数, 但由于共轭梯度算法搜索参数最优解过程受初值影响较大, 且存在迭代次数难确定和局部优化的缺点, 故本文选择粒子群优化(particle swarm optimization, PSO)算法[12-14]优化核函数参数．本文拟提出一种基于粒子群参数优化的动态GPR模型(particle swarm optimization-dynamic Gaussian process regression, PSO-DGPR)预测釜式反应器的出料浓度, 在建模过程中首先考虑模型的阶次, 确定动态模型的输入, 进而建立基于粒子群参数优化的动态高斯过程模型, 并分别与静态模型和未参数优化的动态模型进行对比．

1 高斯过程回归

(1)

(2)

(3)

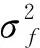
采用最大似然估计方法确定协方差函数参数．对数似然函数可表示为

(4)

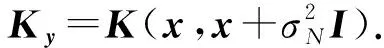
2 标准粒子群算法

粒子群算法中种群由若干个粒子构成, 粒子的个数即种群大小或规模．每个粒子都有一个位置矢量Xi和速度矢量Vi, 其维数代表问题解空间的维数．假设问题的搜索空间是一个d维空间,则第i个粒子的位置矢量和速度矢量分别为Xi=[xi1,xi2,…,xid]和Vi=[vi1,vi2,…,vid]．初始化一群随机粒子,每个粒子在搜索空间中以一定速度飞行, 并通过迭代找到最优解．在迭代过程中, 各粒子通过跟踪粒子本身所找到的最优解Pbest和整个种群目前找到的最优解Gbest这两个“极值”不断进行位置更新．各粒子的速度和位置更新公式如下:

Vid(t+1)=Vid(t)+c1r1(Pbestid(t)-Xid(t))+c2r2(Gbestid(t)-Xid(t)),

(5)

Xid(t+1)=xid(t)+Vid(t+1),

(6)

式中加速因子c1,c2为正常数, 目的是使粒子具有自我总结和向群体中优秀个体学习的能力, 从而向自己的历史最优点及群体的全局最优点靠近,c1,c2用于表示个体经验和群体信息在飞行中的权重时须根据问题分析取值, 通常c1=c2=2;r1,r2为[0,1]之间的随机数．

3 PSO-DGPR建模

3.1 模型定阶

单纯的静态映射无法满足动态过程中模型对输出的预测要求, 故采用动态预测模型进行建模, 同时考虑当前输入对输出的影响以及过去输入和输出对系统当前输出的影响．动态模型在建模时的首要问题是确定模型的阶次, 假设系统的输出y(t)与过去l个输入和k个输出之间服从非线性关系, 则l和k的值即待确定的模型阶次．输入与输出服从如下非线性关系:

y(t)=f(y(t-1),…,y(t-k+1),x(t),…,x(t-l+1))+ε(t),

(7)

其中f(·)为高斯过程拟合的非线性函数,ε(t)为白噪声．

常用的模型选择准则有基于信息论的Akaike信息准则(Akaike information criterion, AIC)[15]和基于Bayes方法的Bayes信息准则(Bayesian information criterion, BIC)[16]等．使用这类准则时, 通过计算不同参数数量模型的AIC值和BIC值来确定最终模型．当模型参数数量增多时, 易导致AIC值过大且模型过于复杂, 从而增大似然函数, 产生过拟合现象．然而, BIC因考虑样本数量, 有效避免了模型精度高所致模型复杂度过高的问题．BIC准则的计算式如下:

(8)

3.2 模型建立

基于粒子群算法参数优化的动态高斯过程回归预测建模步骤如下:

1) 对反应釜内冷却液流量和出料浓度数据进行归一化处理, 并将数据集划分为训练集、验证集和测试集,其中训练集用于训练模型, 验证集用于确定模型阶次,测试集用于检验最终模型的预测性能;

2) 利用BIC确定动态高斯过程回归模型的阶数, 计算输出y(t)分别与过去l个输入和k个输出之间BIC值取最小时对应的阶数l和k值, 即得到最优阶数;

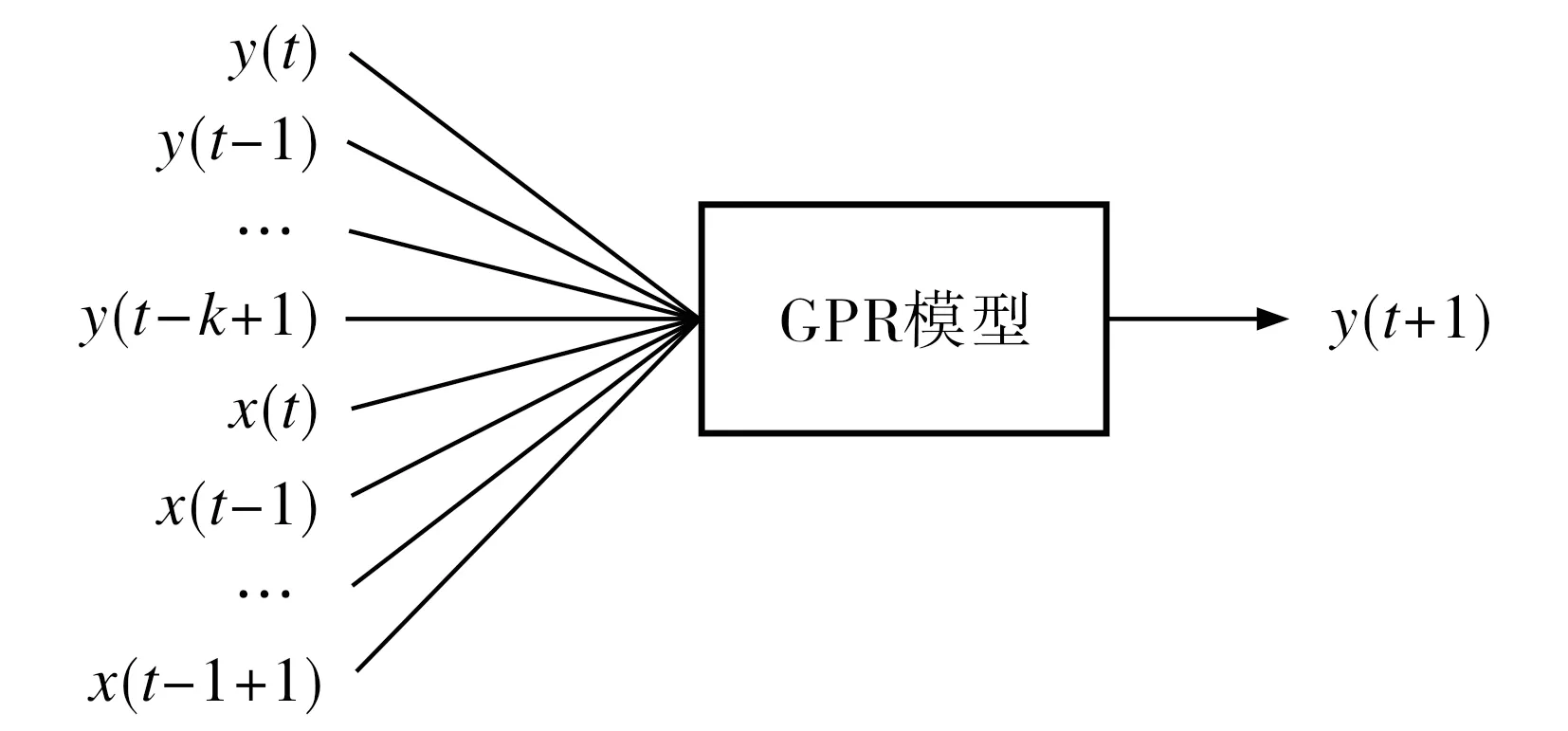
图1 动态GPR模型结构Fig.1 Dynamic GPR model structure

3) 采用粒子群算法优化GPR核函数超参数．初始化粒子群位置和速度,计算每个粒子的适应度．适应度函数取高斯模型中的对数似然函数(4)．根据适应度更新每个粒子的历史最佳位置Pbest和全局最佳位置Gbest, 并根据式(5)(6)更新各粒子的速度和位置．通过判断算法是否达到最大迭代次数或全局最优位置是否满足最小界限来确定算法是否停止;

4) 按照图1所示的模型结构, 利用参数优化的动态高斯过程回归模型对测试样本{y(t-1),…,y(t-k+1),x(t),x(t-1),…,x(t-l+1)}进行预测．

4 实验验证

连续搅拌反应釜数据来源于DaISy数据集．输入为反应釜内冷却液流量q/(L·min-1), 对应的输出分别为出料浓度ca/(mol·L-1)和出料温度T/K, 本文以出料浓度为例作为预测模型的输出．样本的采样时间为0.1 min, 样本个数为7 500, 其中50%样本作为训练集, 剩余的50%样本划分为验证集和测试集．为了对模型的预测性能进行评估, 采用均方根误差(root mean square error, RMSE)、平均绝对误差(mean absolute error, MAE)和平均绝对百分比误差(mean absolute percentage error, MAPE)作为评价标准:

(9)

(10)

(11)

计算GPR模型的阶次, 对应不同阶次的BIC值如图2所示．由图2可见, 当k=3,l=3时, 对应的BIC值均为最小值．由此确定动态模型的输入y(t)=f(y(t-1),y(t-2),y(t-3),x(t-1),x(t-2),x(t-3))+ε(t).

PSO-DGPR模型中种群规模取80, 最大迭代步数为50, 不同阶次对应的预测误差如表1所示．由表1可见, 动态模型的预测结果均优于静态映射模型, 当取3阶历史输入和3阶历史输出作为当前输入(即k=3,l=3)时预测误差最小．静态模型及三阶动态高斯过程模型的预测结果分别如图3～4所示．由图3～4可见, 由于观测样本值较小, 故模型预测误差值较小, 但动态模型的预测误差明显低于静态预测模型的．

图2 阶次k(a), l(b)的BIC值Fig.2 The identification of order k (a) and l (b)

表1 不同阶次下的预测误差

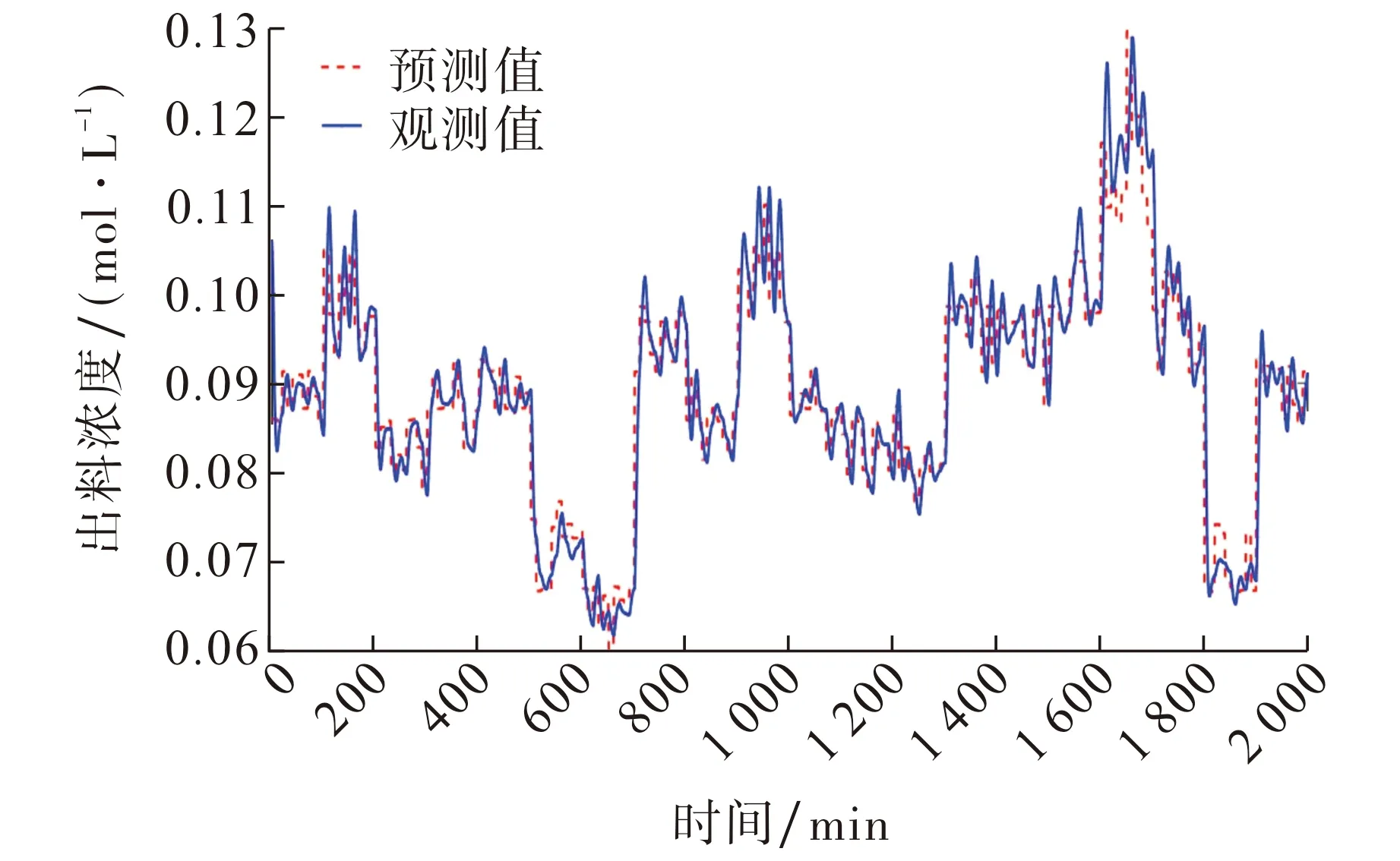
图3 静态映射预测结果Fig.3 Static mapping prediction results

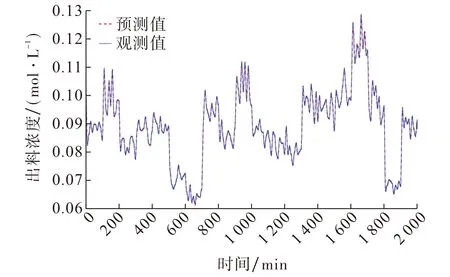
图4 三阶动态高斯过程模型预测结果Fig.4 Prediction results of third-order dynamic Gaussian process model

为了验证本文方法的有效性, 将PSO-DGPR与GPR进行对比实验, 采用梯度下降法求取GPR模型参数, 并选择三阶动态输入作为模型的输入, 预测结果如图5所示．由图5可见, 在数据平滑性较好的情况下,采用动态输入的GPR模型和PSO-DGPR模型均能较好地反映数据变化趋势; 在数据波动较大的情况下, 基于参数优化的PSO-DGPR模型能够更好地应对数据的非线性特性,其灵活性更高,预测效果更佳．

5 结语

本文综合考虑过去的输入和输出对当前输出的影响, 提出了一种基于粒子群算法优化的动态高斯过程回归模型预测CSTR出料浓度．通过BIC方法确定模型阶次, 并构建动态输入．利用粒子群算法代替共轭梯度法优化GPR模型的核函数超参数,构建了基于PSO-DGPR的预测模型．实验结果表明, 所提方法能有效提高CSTR出料浓度预测模型的精度, 对于其他工业时间序列的预测起到一定的启发作用．