一类具有混合扩散的抛物型方程解的正则性

陶益婷, 周 玲

(扬州大学数学科学学院, 江苏 扬州 225002)

由于分数阶算子能够更好地模拟细胞或者种群的扩散[1-2], 近年来许多学者对具有分数阶扩散的各类动力学模型进行了广泛的研究[3-5], 其中解的正则性理论的研究[6-10]在偏微分方程领域备受关注, 也颇具挑战性．2017年, Fernndez-Real等[8]研究了具有非局部扩散的非线性抛物型方程∂tu+(-Δ)su=f(t,x),(t,x)∈(-1,0)×B1, 其中B1是RN中的单位球, 非局部算子(-Δ)su,s∈(0,1)定义为证明了弱解的内部正则性估计, 即: 若f∈L∞((-1,0)×B1), 设α∈(0,1), 且记则可得估计其中常数C仅依赖于N,s和α．受上述研究启发, 本文拟研究RN上带有局部和非局部混合扩散的非线性抛物型方程

(1)

其中u0是RN上的非负Lipschiz连续函数,f(t,x,u)满足条件:

(H1)f: (0,∞)×RN×R+→R满足f(t,x,0)=0且f(t,x,u)关于u∈R+是局部Lipschiz连续的, 即对于任意L>0, 存在一个与L相关的常数K=K(L)>0, 使得对于任意的u1,u2∈[0,L], 有|f(t,x,u1)-f(t,x,u2)|≤K|u1-u2|, (t,x)∈(0,∞)×RN．

对于局部和非局部混合算子,相较于普通的拉普拉斯算子,用经典的能量方法估计弱解的正则性会带来技术性困难.本文将运用反证法,通过构造爆破序列,并结合刘维尔型定理,给出弱解的正则性估计证明．

1 弱解的正则性及证明

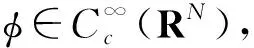
则称u是问题(1)的弱解．

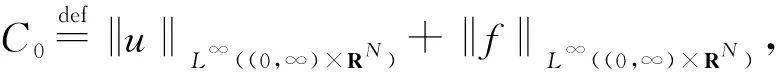
证明 对于任意(t,x), (τ,y)∈(0,∞)×RN且(t,x)≠(τ,y), 定义

假设定理2的结论不成立, 则存在某个θ∈(0,1), 以及方程(1)的弱解序列{uk}, 使得当k→+∞时,

(2)

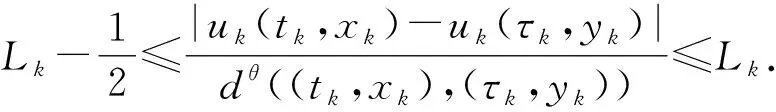
(3)

因0<θ<1, 故当k→+∞时,d((tk,xk),(τk,yk))→0．

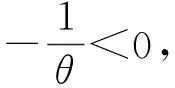
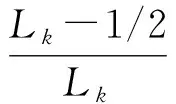
≤1, ∀(x,t), (τ,y)∈Ωk×RN,

故

(4)

再由式(2), 并应用夹逼准则, 得

(5)

进一步, 通过直接计算, 可得

且

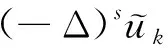
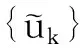
(6)

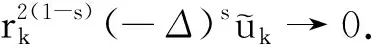
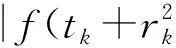
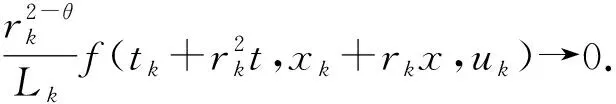
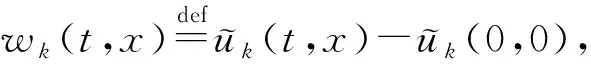
(7)

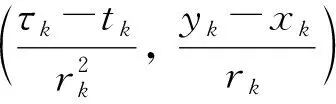
i)Q∞=R×RN．此时, 由于w∞是热方程的一个正解, 根据经典的刘维尔型定理可知,w∞只能是一个常值函数, 与式(7)矛盾．

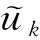
综上, 定理2的结论得证．