界面问题的参数友好型部分罚浸入有限元方法
付灿灿, 纪海峰
(南京邮电大学理学院, 南京 210000)
界面问题是在研究不同材料或相同材料不同状态之间相互作用过程中提出的, 如研究复合材料中的热传导问题[1-3]、弹性界面问题[4]、多相流问题[2,5]等.根据物理守恒定律,界面问题需要在交界面上满足一些跳跃条件, 而不同问题所要满足的界面条件各不相同.众所周知, 除了某些简单的方程外, 偏微分方程的解析求解一般都比较困难[6],因此如何设计快速、有效的数值求解方法对解决实际问题有重要意义.然而,对于界面问题,其复杂的界面跳跃条件给数值方法的设计带来了不小的挑战.目前求解界面问题的数值方法按网格剖分大致可以归为两类:匹配网格方法和非匹配网格方法.所谓匹配网格,是指网格必须界面互相匹配, 即界面只能穿过单元的顶点,不能穿过单元内部.对于这种匹配的网格, 有限元方法能够捕捉真解在界面上的信息,可获得最优逼近性[7-9].然而,对复杂界面, 尤其是三维情形, 生成界面匹配网格非常困难[2], 且当界面随时间移动时在求解过程中该方法需要在每一时间层上重新生成界面匹配网格,这不仅增加了计算量,而且给理论分析带来困难.为了克服上述缺点,有学者提出非匹配网格方法,即界面与网格无关,且允许其以任意方式穿过单元内部.为了获得最优逼近性,非匹配网格方法必须在界面单元(即界面穿过的单元)上进行精细处理[10-13].浸入有限元方法是一类简单有效的非匹配网格方法[14-17],它通过修改界面单元上的基函数获得最优的收敛性,但这种修改带来了一个负面影响,即基函数在界面边(界面穿过的边)上不连续,这给有限元方法带来了相容误差.为了消除该误差, Zhuang等[16-17]提出了部分罚浸入有限元方法.该方法利用间断有限元思想,在界面边上添加额外的惩罚项来惩罚基函数的不连续性,而理论分析指出,罚参数需要充分大才能保证该方法的稳定性,且在实际计算时罚参数需要人为猜测选取,这给实际计算带来麻烦.为克服罚参数选取的缺陷, 针对二阶椭圆界面问题, Ji等[18]提出了参数友好型部分罚浸入有限元方法.该方法通过构造提升算子并把其添加到惩罚项中来保证稳定性,其优点是不需要人为选择罚参数即可保证算法的稳定性.受其启发,本文拟把上述参数友好型部分罚浸入有限元方法推广到抛物界面问题并进行理论分析.在空间方向上将采用参数友好型部分罚浸入有限元方法离散, 而在时间方向上则采用经典的Crank-Nicolson格式, 并借助椭圆投影算子, 推导半离散及全离散格式的最优误差估计.
1 抛物界面问题
设Ω是R2上的凸多边形域,Γ是浸入Ω中的C2光滑界面, 且把Ω分成2个不相交的子区域Ω+和Ω-.不失一般性, 假设Ω-严格包含在Ω的内部, 如图1所示.考虑如下抛物界面问题:

(1)
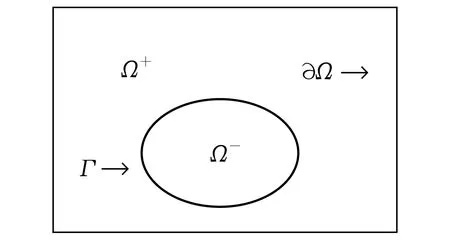
图1 区域Ω=Ω+Ω-ΓFig.1 Domain Ω=Ω+Ω-Γ
(2)
u(·,t)=0, 在∂Ω上,t>0,
(3)
其解满足跳跃条件
(4)
其中n为Γ的单位法向量并指向Ω+; [·]Γ表示在界面Γ上的跳跃, 即[v]Γ=(v+-v-)|Γ, 式中v+=v|Ω+,v-=v|Ω-; 系数β在Ω上为分片常数,即
2 浸入有限元方法
设{Τh}h>0是Ω上的一族三角剖分, 对于每一个单元T∈Th, 定义其网格参数为h=max{hT|T∈Th}, 其中hT为单元T的直径.假设网格满足以下条件:
(H1) 界面Γ与单元的边交点数目不超过2, 除非这条边是界面Γ的一部分.
(H2) 若界面Γ和单元有2个交点, 那么这2个交点一定在这个单元2条不同的边上.
(H3) 剖分Τh是正则的.

图2 界面单元Fig.2 Interface element

在界面单元上的形函数定义为:

(5)
且满足
(6)
其中nh是Γh的单位法向量.令Sh(T)是形函数在界面单元T上组成的空间, 由定义可知, 形函数φ∈Sh(T)及其通量在Γh∩T上连续, 即

(7)
若界面单元的最大角αmax≤π/2, 则函数φ∈Sh(T)由φ(Ai)(i=1,2,3)唯一确定[18], 其中Ai(i=1,2,3)为T的顶点.
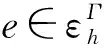
(8)
则式(1)~(3)的半离散方程为
(9)
(10)
其中

(11)
(12)

(13)
(14)
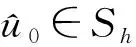

(15)
(16)
3 误差分析
引理1[18]存在正常数C1,C2, 使
Ah(u,v)≤C1|‖u|‖h·|‖v|‖h,
(17)
(18)

Ah(Rhv,ωh)=Ah(v,ωh),∀ωh∈Sh.
(19)



(20)
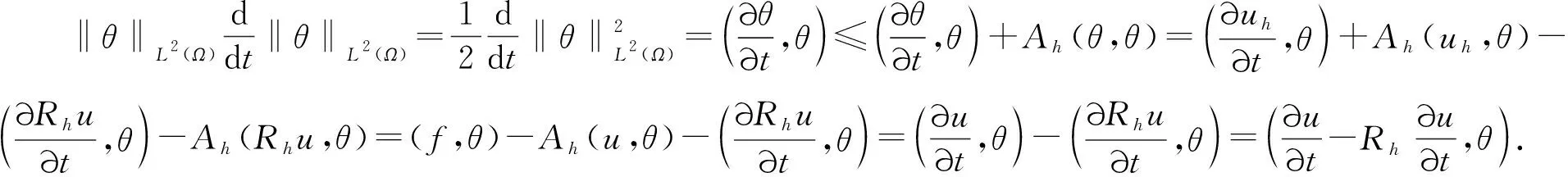
(21)

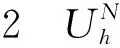
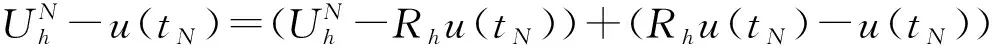
(22)

4 例证
为验证收敛阶, 构造数值算例: 考虑区域Ω=(-1,1)×(-1,1), 界面Γ为半径是0.5, 圆心在(0,0)处的圆, 真解为
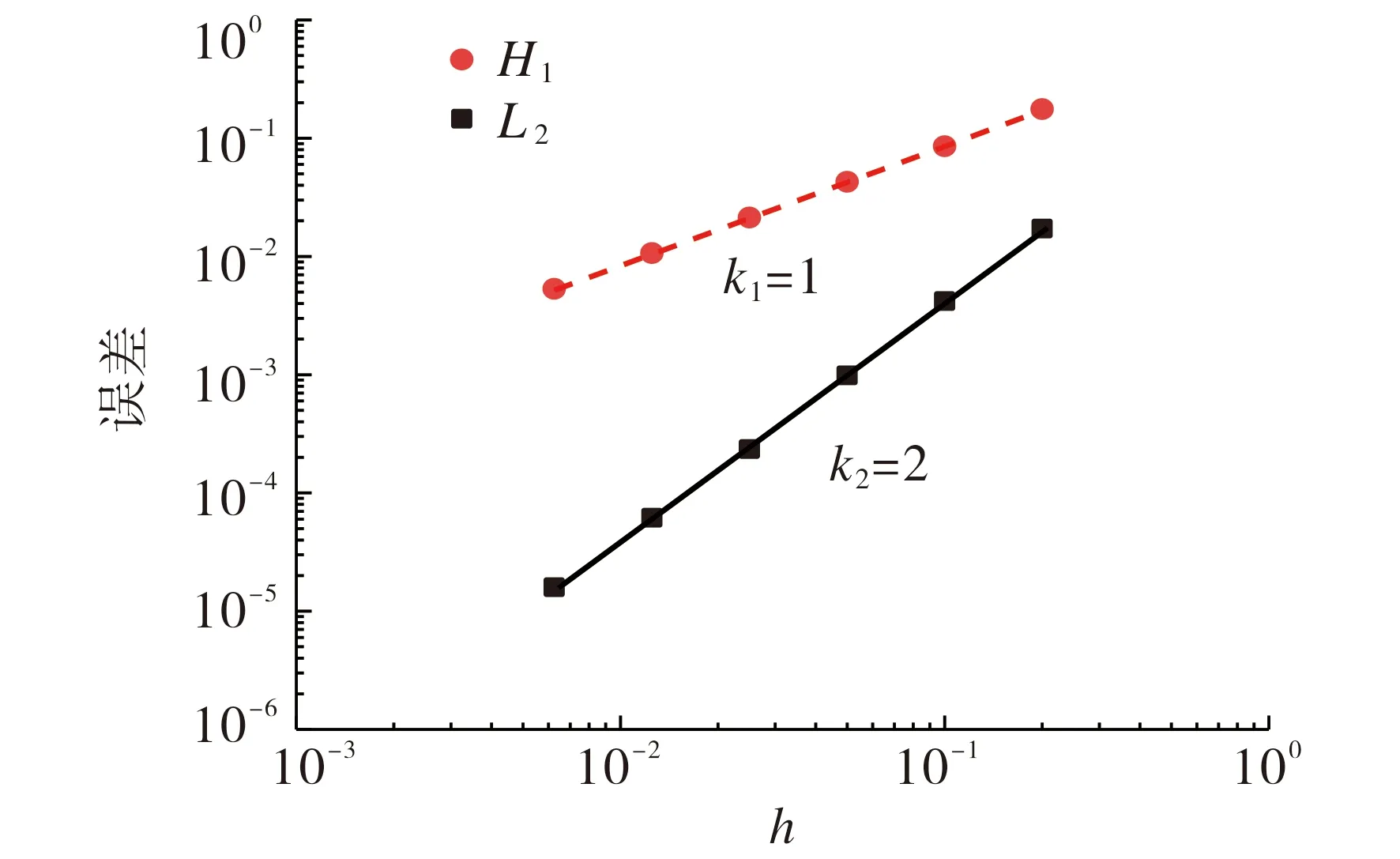
图3 误差收敛示意图Fig.3 Error convergence diagram
其中β+=10,β-=1.
首先将区域分成N×N个矩形, 再把每个矩形沿对角线分成两个三角形, 从而得到一致三角剖分且网格尺寸为2/N.取T=1, 并在时间方向进行等距剖分, 步长选为Δt=h.图3给出了误差收敛示意图.从图3可以看出,L2误差与斜率为2的直线基本一致.根据定理1, 在T时刻有数值解的L2误差应为2阶,验证了本文所提方法的正确性.而H1误差与斜率为1的直线基本一致,故H1误差为1阶收敛.

