半线性时滞不确定动力系统解的存在性

刘 倩, 谢凤艳

(安阳学院计算机科学与数学学院, 河南 安阳 455000)

模糊微分方程是近年来发展起来的一个新的研究领域．研究模糊微分方程的基本方法通常采用H-导数, 但Hüllermeier[1]和Diamond[2]等发现在H-导数意义下模糊微分方程初值问题(fuzzy initial value problem, FIVP)解的支撑集较大, 难以反映常微分方程初值问题解的丰富性质,为了克服这一缺陷,他们首先研究了在微分包含意义下模糊微分方程的初值问题; 薛小平等[3]吸收了其思想方法,并在微分包含意义下给出了FIVP大解与解的包含关系; 陈明浩等[4-5]在微分包含意义下考虑模糊微分方程的两点边值问题和周期问题,得到了二阶不确定动力系统两点边值问题、半线性不确定动力系统周期问题解的存在性; 戴睿等[6-7]运用Green函数给出了不确定动力系统周期问题解的存在性和稳定性; Khastan等[8]研究了广义导数意义下模糊微分方程问题; 席艳丽[9]和刘锡平[10]等研究了分数阶模糊微分方程解的存在性．这些研究极大地丰富了模糊微分方程问题的成果,然而作为微分方程的另一个重要分支,时滞微分方程能准确、合理地描述现实世界中的时滞运动现象．张孟孟[11]利用压缩映像原理得到一类时滞模糊微分方程初值问题解存在的一个充分条件; 刘娟等[12]在广义导数意义下运用弱压缩映射的不动点定理将半线性时滞模糊微分方程解的问题转化为算子的不动点存在性问题, 给出了该方程上下解的存在性定理．时滞模糊微分方程具有广泛的应用背景和深刻的理论意义,本文拟在微分包含意义下将时滞模糊微分方程转化为微分包含族,在满足Lipschitz连续条件下利用不动点定理,并结合集值分析和泛函分析理论,给出半线性时滞不确定动力系统解的存在性定理,丰富时滞微分方程的成果,为其在工程学、经济学、物理学、生物学等领域内的广泛应用提供理论支持．

1 预备知识

定义1[3]记D1={u|u:R→[0,1]}满足: i)u是正规的模糊集, 即存在ξ∈R, 使u(ξ)=1; ii)u是上半连续函数; iii) 支撑集[u]0=cl{ξ∈R|u(ξ)>0}在R中有界．

定义2[3]记E1={u|u:R→[0,1]}满足: i)u∈D1; ii)u是凸模糊集, 即u(λξ1+(1-λ)ξ2)≥min{u(ξ1),u(ξ2)}(∀ξ1,ξ2∈R,∀λ∈[0,1])．∀u∈E1称为一维模糊数(简称模糊数),E1称为模糊数空间．

注1显然, 由定义知∀u∈E1,[u]α={x∈R|u(x)≥α}(∀α∈[0,1])为非空有界闭集．

定义3[2]Ec={u∈E1|u1(α)=min[u]α和u2(α)=max[u]α在I=[0,1]上连续, 0≤α≤1},称u∈Ec为连续的模糊数．显然,Ec⊂E1．

定义4[13]设Y,Z是Hausdorff拓扑空间, 称集值映射G:Y→2z∅是上半连续的, 若对于Z的任何非空闭子集C, 集合G-(C)={y∈Y|G(y)∩C≠∅}是Y的闭子集．

定理1(Kakutani不动点定理)[14]设K是X的非空紧凸子集, 若F:K→Pkc(K)是上半连续的, 则F有不动点, 即存在x*∈K使x*∈F(x*)．

定理2[5]设X是可分的B*空间, 那么X*上的任意有界列{fn}必有*弱收敛子列．

定理3(Arzela-Ascoli定理)[5]设M是一个紧的距离空间,C(M)表示M→R的一切连续映射全体, 为了F⊂C(M)是列紧集, 必须且仅须F是一致有界且等度连续的函数族．

定理4[4]令CA([a,b],R)表示[a,b]上绝对连续函数的集合, 那么x∈CA([a,b],R)⟺x∈W1,1([a,b],R)．

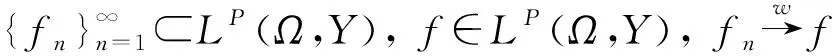
2 主要结论

半线性时滞模糊微分方程

(1)

将其考虑为一族微分包含

(2)

其中f:J×R→Ec,J=[t0-τ,t0+a],t0-τ≥0,λ,a>0．

定义5若u(t)是绝对连续的, 且满足系统(2), 则称u(t)为系统(2)的解．令Sα(J;t)={u(t)|u(t)是系统(2)的解}(α∈[0,1])是系统(2)的解集, 若存在v(t):J→D1使[v(t)]α=Sα(J;t)(t∈J,α∈[0,1]), 则称v(t)(t∈J)为系统(1)的解．

定理6假设f:J×R→Ec满足:

i)f在J×R上连续;

ii) 存在M>0, 对任意的(t,ξ)∈J×R,‖f(t,ξ)‖≤M成立;

iii) 对任意的(t,ξ),(t,η)∈J×R, ‖f(t,ξ)-f(t,η)‖≤L‖ξ-η‖成立, 其中Lipschitz常数L> 0, 则系统(2)的解集Sα(J,t)非空且一致有界．

证明 1) 令系统(2)为

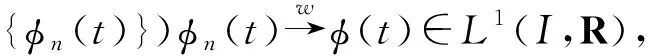
∀φ1(t),φ2(t)∈U(u(t)), 即φ1(t),φ2(t)∈Fα(t,u(t-τ)), ∀λ∈[0,1], 有λφ1(t)+(1-λ)φ2(t)∈Fα(t,u(t-τ))成立, 即U(u(t))为凸集．

∀φ(t)∈U(u(t)), 故φ(t)∈Fα(t,u(t-τ)), 则‖φ(t)‖≤dH(Fα(t,u(t-τ)),0)=‖f(t,u(t-τ))‖≤M, 即U(u(t))一致有界．

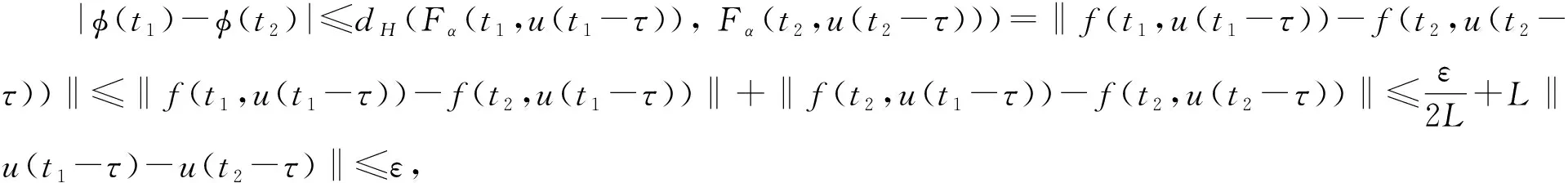
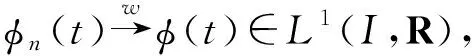
2) 定义算子L:W1,1(I,R)→L1,1(I,R), 且L(u)=u′+λu．易得L为可逆线性算子且L-1:L1(I,R)→L1(I,R)是紧算子, 则L-1U是上半连续且将任何有界集映射成列紧集．由定理3知,L-1U:W1,1(I,R)→Pkc(W1,1(I,R))上半连续的, 且U(u(t))为W1,1(I,R)非空紧凸闭子集．由定理1知,L-1U存在不动点u(t)∈L-1U(u(t)), 则L(u)=u′+λu∈U(u(t)), 有u′(t)+λu(t)∈Fα(t,u(t-τ)),t∈I．又u(t)=u0,t∈[t0-τ,t0], 故u(t)为系统(1)的解, 即Sα(J,t)非空．

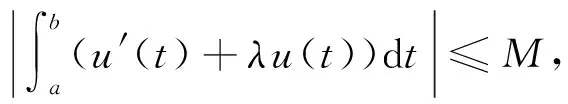
定理7假设f:J×R→Ec满足:

i)f在J×R上连续;

ii) 存在M>0, 对任意的(t,ξ)∈J×R,‖f(t,ξ)‖≤M成立;

iii) 对任意的(t,ξ),(t,η)∈J×R,‖f(t,ξ)-f(t,η)‖≤L‖ξ-η‖成立, 其中Lipschitz常数L> 0, 则存在系统(1)的解v:J→D1,使[v(t)]α=Sα(J;t),α∈[0,1]．

3 例证

设J=[0,2],f(t)=et+1w(t∈[1,2]),u(t)=w(t∈[0,1]), 其中w∈Ec,α∈[0,1],[w]α=[α,2-α]．显然,f(t)满足定理6的3个条件且t0=1．此时, 半线性时滞不确定动力系统为

可变为

4 结论

本文在微分包含意义下讨论半线性时滞模糊微分方程的初值问题, 弥补了在H-导数意义下半线性时滞模糊微分方程解存在的苛刻性, 也扩宽了在广义导数意义下时滞模糊微分方程解存在的局限性,为模糊微分方程解的存在提供了更为简单直接的方法和更为广泛的空间, 而且这种方法在模糊微分方程的边值问题和周期问题都有很大的应用价值．下一步的研究主要集中在半线性时滞不确定动力系统的稳定性等方面．