巧用旋转变换求解线段(和)的最值问题

罗强华

(重庆市奉节县巴蜀渝东中学,404600)

在初中几何试题中,我们时常遇到求解某条线段或某两条线段之和的最值问题.解决这类问题的常用方法是通过旋转变换作出恰当的辅助线,并借助全等三角形或相似三角形,将相关线段置于某一三角形中,再根据三角形的三边关系,即“三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边”来求解.下面举例说明.

一、以三角形为载体

1.构造全等三角形

例1如图1,等边∆ABC的边长为2,点D为BC边的中点,连结AD,点E,F分别是AD,AC上的两个动点,且AE=CF,求BF+CE的最小值.

分析由等边∆ABC及AE=CF,通过旋转变换构造全等三角形将BF和CE这两条分散的线段集中到一个三角形当中,再借助三角形的三边关系来解决问题.

解如图1,将线段AC绕点A顺时针旋转90°到AG,连结GE,GC.

∵D为等边∆ABC的BC边的中点,

∴AD⊥BC,∴∠ACD+∠CAD=90°,

∴∠GAE=∠ACD.

∵AG=BC,AE=CF,

∴∆AGE≌∆CBF,∴GE=BF.

说明当图形中的线段比较分散时,可以通过旋转变换将分散的线段集中在一个三角形中来解决问题.

2.构造相似三角形

例2[1]如图2,在Rt∆ABC中,∠BAC=90°,∠ACB=30°,点P为∆ABC所在平面内的一点,且点P到∆ABC的顶点A,B的距离分别为PA=6,PB=8,求PC的最值.

分析由图形可知,PA,PB,PC是分散的,从而想到通过旋转变换将三条线段集中到一个三角形当中,再通过三角形的三边关系来求PC的最值.

又∵∠CAP′=∠BAP,

在∆CPP′中,由三角形的三边关系,可得CP′-P′P≤PC≤CP′+P′P(当且仅当C,P,P′三点共线时,取“=”),

二、以四边形为载体

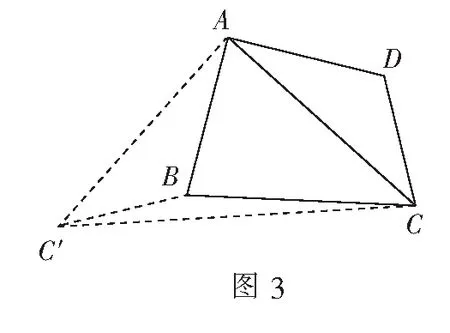
分析由共端点的等线段AB和AD,想到通过旋转将CD,CB集中到一个三角形当中,则问题迎刃而解.

解如图3,将∆ACD绕点A顺时针旋转90°至∆AC′B,连结CC′,则CD=C′B,∆ACC′是等腰直角三角形.

在∆BCC′中,由三角形的三边关系,可得C′B+CB≥CC′=10(当且仅当B,C,C′三点共线时,取“=”),

即CD+CB≥1,

∴CD+CB的最小值为10.

故答案为10.

三、以正方形为载体

例4如图4,在∆ABC中,BA=1,BC=2,以AC为边作正方形ACDE,使E,B两点落在直线AC的两侧,当∠ABC变化时,求BE的最大值.

分析由正方形具有共端点的等线段想到将∆ABE绕点A旋转,得到等腰Rt∆ABB′,可确定BB′为定值,再在∆BB′C中运用三角形的三边关系便能求解.

解如图4,将∆ABE绕点A顺时针旋转90°至∆AB′C,则BE=B′C,∆ABB′为等腰直角三角形,

四、以半圆为载体

例5[2]如图5,已知半圆O的直径为2,射线AF与半圆O相切于点A,长为1的线段CD在半圆上滑动,E是射线AF上的一动点,则BC+DE的最小值为______.

分析由半圆的半径相等,想到通过旋转变换将BC和DE这两个分散的线段集中到一个三角形当中,再运用三角形的三边关系可求得BC+DE的最小值.

解如图5,连结OC,OD.

由题意,可得等边∆COD,

∴∠DOC=60°.

将∆BOC绕点O逆时针旋转60°至∆MOD,连结EM,则∠BOM=60°.

在∆DEM中,由三角形的三边关系,可得DM+DE≥EM(当且仅当D,E,M三点共线时,取“=”),

∴BC+DE≥EM.

过点M作MN⊥AB于点N,则ON=

∵射线AF与半圆O相切于点A,

∴AB⊥AF,