剖析中考错解 实现思维分享*——2021年广州市中考数学第22题的错解分析及纠错策略

张河源

(广东省广州市增城区教师发展中心，511300)

错解是学生学习过程中十分宝贵的资料,也是教师教学过程中有效的教学资源.教师利用好错解资源，仔细分析错因，就能既帮助学生根治病症，又有助于教师自己提高教学水平.笔者利用阅卷之便，全面收集与分析广州2021年中考数学第22题的典型错解,进行归因分析，乐与同行分享．

一、原题呈现

如图1,在四边形ABCD中,∠ABC=90°,点E是AC的中点,且AC=AD.

(1)尺规作图:作∠CAD的平分线AF,交CD于点F,连结EF,BF;

(保留作图痕迹,不写作法.)

(2)在(1)所作的图中,若∠BAD=45°,且∠CAD=2∠BAC,求证:∆BEF为等边三角形.

二、简解

(1)图2为所求作的图形.

(2)证明:∵∠BAD=45°,

∠CAD=2∠BAC,

∠CAD+∠BAC=∠BAD,

∴∠CAD=30°, ∠BAC=15°.

∵AC=AD,A

F是∠CAD的平分线,

∴∠FAE=∠FAD=15°,∠AFC=90°.

∴∠BAF=30°.

∵∠AFC=90°,∠ABC=90°,

∴∠AFC+∠ABC=180°,

∴点B,A,F,C四点共圆,AC为直径.

∴EF=EB,∠BEF=2∠BAF=2×30°=60°,

∴∆BEF为等边三角形.

三、 典型错误与分析

第(1)问尺规作图,比较简单,学生作答较好.主要错误出现在第(2)问,笔者调阅试卷，发现主要有以下五种典型错解．

错解1(2)证明:∵∠BAD=45°,∠CAD=2∠BAC,

∠CAD+∠BAC=∠BAD,

∴∠CAD=30°， ∠BAC=15°.

∵AC=AD,AF是∠CAD的平分线,

∴∠FAE=∠FAD=15°,

∴∠BAC=∠FAC=15°,

∴EB=EF.

错因分析学生对“点到直线的距离”理解出错,误把“EB，EF”当成“∠BAC的平分线一点E到∠BAC的两边AB，AF的距离”,导致出现错误结论“EB=EF”．

错解2

(2)证明:∵∠BAD=45°,

∠CAD=2∠BAC,

∠CAD+∠BAC=∠BAD,

∴∠CAD=30°， ∠BAC=15°.

∵AC=AD,AF是∠CAD的平分线,

∴∠FAE=∠FAD=15°,

∴∠BAC=∠FAC=15°,

∴AC是∠BAC的角平分线.

∵∠ABC=90°,∴CB=CF.

错因分析学生对“角平分线的性质定理”理解出现偏差,误把一个平分“AC是∠BAC的角平分线”和一个垂直“∠ABC=90°”当成“角平分线性质定理中的两条件一平分两垂直”,导致出现错误结论“CB=CF”．

错解3

(2)证明:∵∠BAD=45°,

∠CAD=2∠BAC,

∠CAD+∠BAC=∠BAD,

∴∠CAD=30°, ∠BAC=15°.

∵AC=AD,AF是∠CAD的平分线,

∴∠FAE=∠FAD=15°,

∴∠BAC=∠FAC=15°.

在 Rt∆ABC中,点E为AC的中点，

∴以点E为圆心,BE为半径作⊙E,

∴点B，A，F，C四点共圆.

∴EB=EF,∠BEF=2∠BAF=2×(∠BAC+∠CAF)=2×30°=60°.

∴∆BEF为等边三角形.

错解4

(2)∵∠BAD=45°,且∠CAD=2∠BAC,

再由∠CAD+∠BAC=∠BAD,

得∠BAC=15°,∠CAD=30°.

∵∠ABC=90°,点E是AC的中点,

∴∠ABE=∠BAE=15°.

在∆ABE中,

∠BEC=∠ABE+∠BAE=30°.

∵AC=AD,AF是∠CAD的平分线,

∴CF=DF,即F为CD中点.

∵点E是AC的中点,

∴∠EFA=∠FAD=15°.

∵AB=AF，

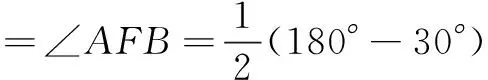
=75°，

∴∠EFB=∠AFB-∠EFA=60°.

∴EF=BE.

∴∆BEF为等边三角形.

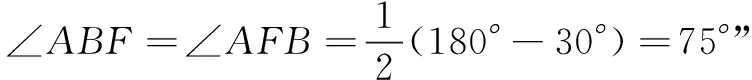
错解5

(2)证明:∵∠BAD=45°,

∠CAD=2∠BAC,

∠CAD+∠BAC=∠BAD,

∴∠CAD=30° ∠BAC=15°.

∵AC=AD,AF是∠CAD的平分线,

∴∠FAE=∠FAD=15°,

∴∠BAC=∠FAC=15°.

在∆ACF和∆ADF中，

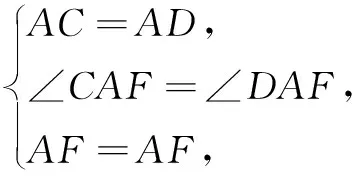
∴∆ACF≌∆ADF，

∴∠AFC=∠AFD=90°，

∴AF⊥CD.

在∆ABC和∆AFC中，

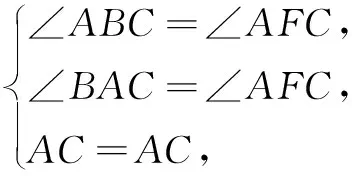
∴∆ABC≌∆AFC，

∴BC=FC，AB=AF，

∴AC是BF的垂直平分线，

∴EB=EF.

四、干预错误发生的应对策略

出错不可怕,重复出错才可怕．为避免学生在类似的数学问题上再出错误,教师务必深入剖析数学易错点出错的成因,抓住问题的症结,采取有效的教学手段提前干预．针对广州市中考21题出现的五种典型错误及其原因,我们提出提前干预错误发生的应对策略建议．

针对错误1,建议注重数学概念的教学

数学思维形式的判断与推理是以定理、法则、公式的方式表现出来,而数学概念则是基础．正确地理解并灵活运用数学概念,是掌握数学基础知识和运算技能、发展逻辑论证和空间想象能力的前提．数学概念教学应鼓励学生经历观察、操作、想象、推理、表达等思维活动．

例如,教师在教学“点到直线的距离”.

首先,让学生画一条直线l与直线l的一点P,连结点P与直线l上各点O，A1，A2，A3….其中PO⊥l(如图3).

其次,让学生比较线段PO,PA1,PA2,PA3…的长短,并问学生,这些线段中,哪一条最长?哪一条最短?让学生充分感受知识的生成．

再次,让学生给出概念“直线外一点到这条直线的垂线段的长度,叫做点到直线的距离”,强调关键词“垂直的线段”,让学生识图,画图,辩图,在画图中理解线段与线段的数量关系与位置关系,增强对图形的观察能力和鉴赏能力,培养学生几何直观的素养．

最后,给出其性质“垂线段最短”．

针对错误2，3,建议注重几何定理的教学

几何定理是证明过程的基本单位与逻辑推理的依据,教师在教学中可采用“自主探究法”．

如教师教学“角的平分线的性质定理”.

首先让学生画出∠AOB的平分线OC,在OC上任取一点P,过点P画出OA，OB的垂线,分别记垂足为D，E,测量PD，PE并作比较,得到什么结论?在OC上再取几个点试一试,通过以上测量,你发现了角的平分线的什么性质?让学生猜想角的平分线的性质,写出命题“角平分线上的点到角的两边的距离相等”．

其次,让学生找出命题的题设与结论,题设用直线标识,结论则波浪线标识,并突出本质部分“角的平分线上的点到这个角两边的距离”,根据题设与结论写出“已知”和“求证”,并要求学生自主探究命题的证明过程,堂上分享．

再次,让学生用几何语言写出定理的内容.

∵∠AOP=∠BOP,PD⊥OA,PE⊥OB，

∴PD=PE.

教师强调定理的条件是“一平分两垂直”,结论为“一相等”,尤其是“垂直”,为此教师可以设置一些反例让学生辩识,达到较佳效果．

最后,用类似的方法让学生“自主探究”定理的逆定理“角的内部到角的两边的距离相等的点在角的平分线上”,进一步体验定理与逆定理的学习过程,加深定理之间的区别与联系．

又如，教师在教学“三角形外接圆”.

首先,给学生思考“经过不在同一条直线上的三个点A，B，C能不能作圆,如果能,可以作出符合条件的圆有多少个?如何确定所作圆的圆心与半径?如果不能,说明理由．”让学生自主探索,然后小组交流,展示探究成果．

其次,教师利用几何画板,画出经过已知点A，B，C的圆,讲清画图原理“因为所求的圆要经过A，B，C三点,所以圆心到这三个点的距离必须要相等,根据线段的垂直平分线的性质定理可以得到,这个圆心必须在线段AB的垂直平分线上,又要在线段BC的垂直平分线上”．然后由学生动手画图,并呈现画图的步骤．

再次,师生互动交流后一致得出定理“不在同一条直线上的三个点确定一个圆”．进而得出任意一个三角形都有外接圆．

最后,把结论“任意一个三角形都有外接圆”拓展,请问“任意一个四边形是否都有一个外接圆?”让学生自主探究、动手操作、猜想,辩论,学生畅所欲言,教师利用几何画板对学生的结论进行一一验证,去伪存真,形成一致结论“只有对角互补的四边形才有其外接圆”．

针对错误4，5,建议注重数学逻辑推理的训练

有的学生在推理过程中,常常会出现跳步、条理不清、推理不顺等.教师平时的教学中要重视学生逻辑推理能力的训练及空间想象能力的培养．