采煤机自适应调高控制策略

王雅东，赵丽娟,2，张美晨

(1.辽宁工程技术大学 机械工程学院，辽宁 阜新 123000；2.辽宁省大型工矿装备重点实验室，辽宁 阜新 123000)

采煤机是综采工作面的核心装备，其智能高效截割是实现综采工作面智能化无人开采的基础保障，而采煤机截割滚筒的自适应调高在其中扮演重要角色，采煤机在进行综采作业时主要是利用液压系统对摇臂及滚筒高度进行调节，以适应不同厚度煤层的开采要求，调高液压系统在工作时要承受摇臂和滚筒自重及滚筒截割作业时所受到的冲击载荷作用，加之煤矿井下复杂的煤层赋存条件，导致采煤机的调高液压系统故障频发，给煤矿井下的正常综采作业造成了极大的困扰，因此，伴随综采工作面智能化无人开采要求的提出，滚筒高度自适应调节是目前学者们的研究热点之一。钟伟才基于PID电液比例液压系统机液耦合仿真模型，通过协同仿真研究了采煤机实验台在不同负载条件下，调高控制系统的响应快速性与滚筒跟踪目标轨迹的准确性。汪亮培利用单神经元与PID相结合的控制方法对电液比例调高系统进行研究，结果显示该控制方法具有较强的鲁棒性。毛君等提出了一种新型萤火虫算法优化PID控制器的控制策略，优化后的PID控制器对调高系统具有良好的控制性能。赵丽娟等前期采用模糊PID实现对采煤机调高系统的控制，与常规PID控制相比在快速性、稳定性、抗干扰能力等方面均有提高。煤岩截割状态的精准识别是实现滚筒高度自适应调节的前提，近些年来，学者们采取滚筒截割振动时域特性分析法、模糊识别技术、光谱分析识别技术、红外热像技术、基于多传感信息融合法等不同手段进行了大量研究，对煤岩识别技术的发展起到了积极的推动作用。将一维特征信号转换为时频谱图用以对工程故障诊断的研究也为煤岩识别提供新思路。

采煤机是机-液-控一体化设备的典型代表，各组成单元之间存在着多重耦合关系，单一领域的建模仿真与分析难以完成煤机性能的综合分析任务，而多领域建模与协同仿真方法显现出了更强的生命力，其中基于接口的多领域建模与协同仿真方法旨在将机械、液压、控制等不同学科领域的模型搭建成一个能够协同仿真、可耦合算法设计的仿真系统模型，将其应用在煤岩截割过程中采煤机自适应调高性能分析时存在以下3个优势：

(1)直接从EDEM-RecurDyn双向耦合仿真软件生成机械系统动力学方程，不仅简化了繁琐的建模过程还使得计算结果更加精确。

(2)直接利用Simulink模块搭建复杂的控制系统模型并实现对机械和液压系统的控制，有效解决了机械和液压系统自带的控制系统性能差的劣势。

(3)仿真过程虽略微复杂，但其反映的结果与实际更为契合，有效提高了研究的可信度。

采煤机截割、破落煤岩是一个复杂的，具有非平衡、时变性和强耦合特点的过程，采煤机实际调高控制信号需根据煤层赋存条件和煤岩识别结果自适应调整，以此分析自适应调高系统性能更贴合于实际。据此笔者基于虚拟样机技术、深层卷积神经网络模型和深度强化学习算法，采用多领域软件建模与协同仿真方法，搭建了采煤机自适应调高机-液-控一体化系统模型并进行仿真，仿真可以针对不同的工况进行反复试验，极大降低研发成本，提高研究的安全性和可靠性，并通过试验对其调高过程进行验证，有效提高采煤机对复杂煤层的适应性、促进煤矿智能化的发展进程。

1 采煤机调高液压系统原理

采煤机自适应调高液压系统结构如图1所示。

图1 采煤机自适应调高液压控制系统结构

结合电液比例控制技术，使用电液比例换向阀，基于检测的位移反馈信号与目标控制信号差值作为自适应控制器的输入来改变电磁阀的极性和大小，进而控制流过换向阀液体的流向和流量，实现对调高油缸的无级调速，调节滚筒升降，可以使调高缸平稳地加速或者减速，减少了系统的振动冲击和噪声的危害。在无杆腔回油路上增加单向节流阀和单向阻尼器抑制摇臂下调抖动现象；将单向阀与顺序阀结合构成双向平衡阀，实现调高油缸的锁紧与安全保护功能。

图2为采煤机调高液压系统几何关系简图，设活塞由运动到，滚筒由最低点运动到最高点，为调高油缸转过的角度，(°)；为调高油缸活塞伸出速度，mm/s；为滚筒处于最低点时调高油缸活塞端部距调高油缸与机身耳环铰接点的距离，mm；为小摇臂的长度，mm；为滚筒摇臂的长度，mm；为机身下耳环铰接点与摇臂上耳环铰接点距离，mm；和分别为滚筒处于最低点和最高点时活塞与小摇臂之间的夹角，(°)；为摇臂和转过的角度，(°)；和分别为∠和∠的大小，(°)；为液压缸活塞杆伸出过程所经过的时间；⊥和‖分别为滚筒处于最低点时，活塞伸出速度沿小摇臂方向和垂直于小摇臂方向的速度分量，mm/s；⊥和‖分别为滚筒处于最高点时，活塞伸出速度沿小摇臂方向和垂直于小摇臂方向的速度分量，mm/s；，和分别为滚筒处于最高点时，滚筒运动合速度、沿水平方向和竖直方向的速度分量，mm/s；为滚筒极限调节高度，mm。

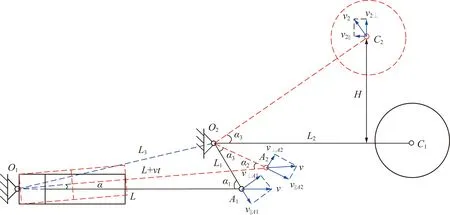
图2 采煤机调高液压系统简化示意

由图2可知采煤机滚筒高度在竖直方向的调节速度为

=cos

(1)

=⊥

(2)

由式(2)得

=⊥

(3)

⊥=sin

(4)

(5)

=-

(6)

(7)

根据式(1)～(7)可得到活塞伸出速度和采煤机滚筒高度在竖直方向的调节速度之间的关系为

(8)

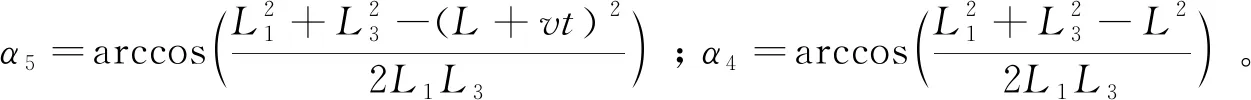
由式(8)可知，活塞伸出速度和采煤机滚筒高度在竖直方向的调节速度呈非线性关系，并且随着活塞伸出位移的增大，滚筒在竖直方向的调节速度逐渐减小。

2 采煤机自适应调高系统多领域协同建模

利用Pro/E及RecurDyn建立采煤机调高系统刚柔耦合动力学仿真模型，利用EDEM建立离散元煤壁模型，基于DEM-MFBD接口构建EDEM-RecurDyn双向耦合仿真调高机械系统模型，基于AMEsim建立调高机构液压系统模型。

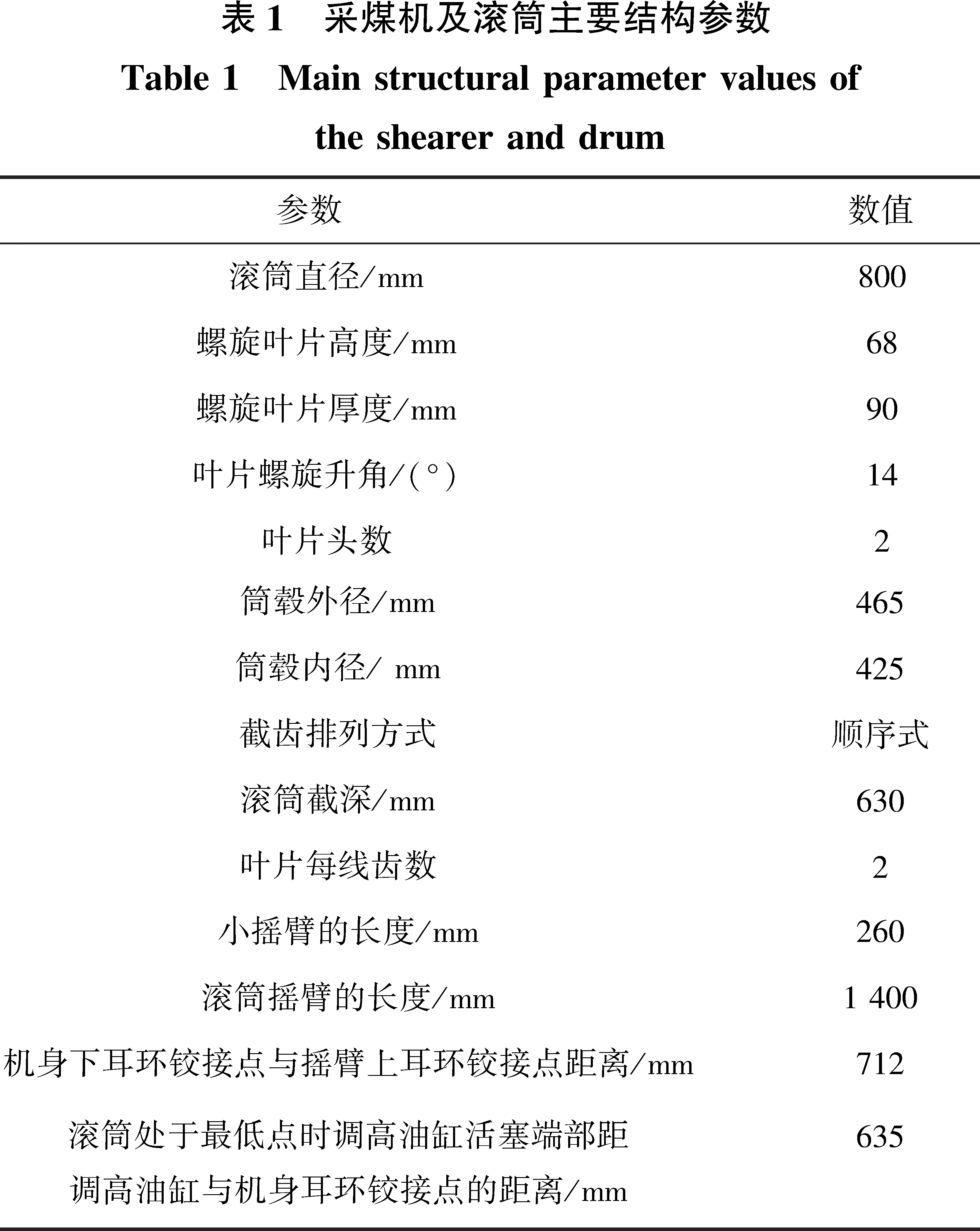
以MG2×55/250-BWD型薄煤层采煤机为工程对象，其主要结构参数见表1。基于Pro/E建立各零部件三维实体模型并进行装配，最终得到总装实体模型如图3所示。

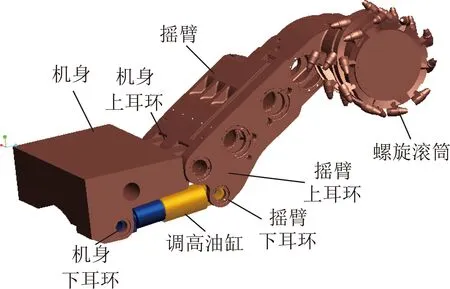
图3 采煤机调高机构三维实体模型

将调高机构三维实体模型导入RecurDyn软件中，并根据主要零部件间的相对运动关系添加约束，见表2。

表2 采煤机调高机构关键部件约束关系

由于煤层赋存条件复杂，在截割、破碎煤岩过程中，螺旋滚筒将受到来自煤岩体的冲击、非线性载荷而存在变形，尤其是螺旋滚筒及截齿直接参与截割，其变形程度更加明显，应对其进行柔性化处理，最终建立采煤机调高机构刚柔耦合动力学仿真模型如图4所示。

图4 采煤机调高机构刚柔耦合动力学仿真模型

基于兖矿煤业集团杨村煤矿4602工作面煤层赋存条件，获得离散元煤壁建模所需的力学性质参数见表3，并设计表4所示的4种典型工况进行采煤机自适应调高系统性能研究。

表3 煤岩体物理力学参数

表4 典型工况

根据实际煤岩体特性，颗粒与颗粒之间选用Hertz-Mindlin with bonding模型；基于BP神经网络，分别采用单轴压缩和巴西劈裂数值模拟试验进行参数标定获得煤岩颗粒间黏结参数，见表5。

表5 颗粒之间黏结参数

使用半径为12 mm的颗粒建立煤壁模型，根据表4中4种典型工况，建立EDEM煤壁模型如图5所示，以此来模拟不同顶板厚度下滚筒自适应调高截割工况，以工况1条件下建立的煤壁模型为例，实现与采煤机调高机构刚柔耦合动力学仿真模型的耦合，设置采煤机牵引速度=4 m/min、滚筒转速=90 r/min进行仿真，仿真模型如图6所示。

图5 不同工况下EDEM煤壁模型

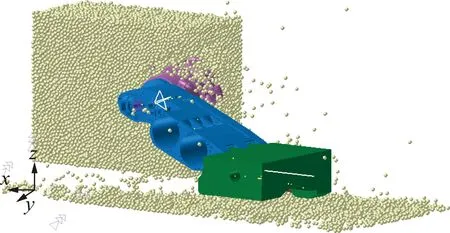
图6 EDEM-RecurDyn双向耦合调高机械系统仿真模型

考虑到后续研究需以EDEM-RecurDyn耦合仿真获取特征信息为基础，本文从理论计算和试验台试验2个方面对EDEM-RecurDyn耦合仿真的可行性与结果准确性进行验证。首先，利用课题组开发的采煤机工作机构载荷计算及参数优化软件对与基于EDEM-RecurDyn耦合仿真相同工况的滚筒受载进行准确性验证，结果见表6，受载均值、波动系数、均方根值的相对误差分别为4.77%，4.54%，3.29%；利用试验台试验验证基于EDEM-RecurDyn耦合仿真获得的滚筒振动特性的准确性，提取滚筒稳定截割状态下在截割阻力方向上的振动特性的仿真与试验曲线，结果如图7所示，振动特性特征值见表7，其中振动特性的试验值通过安装于滚筒上的无线振动加速度传感器获得，传感器布置如图8所示。

图7 基于仿真和试验的滚筒振动特性

图8 无线振动加速度传感器及其布置

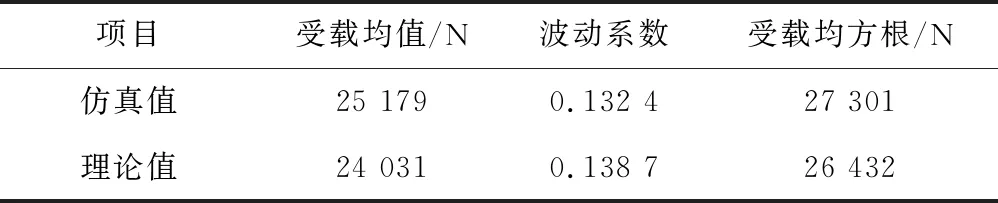
表6 滚筒受载特征值对比

对比分析表6中滚筒受载特征值、图7中滚筒振动特性曲线及表7滚筒截割阻力方向振动加速度时域信号特征值可知，滚筒受载特征值的最大相对误差为受载均值间的相对误差，仅为4.77%，处于合理范围内；滚筒振动特性波形相近，均在-19 000～18 000 mm/s波动，通过采样点数据导出计算得到仿真及试验条件下滚筒截割阻力方向振动加速度特征值的最大相对误差仅为6.65%，处于合理范围内；综上所述，无论是从滚筒受载亦或滚筒的振动特性角度均能够验证基于EDEM-RecurDyn耦合仿真的可行性与结果准确性。

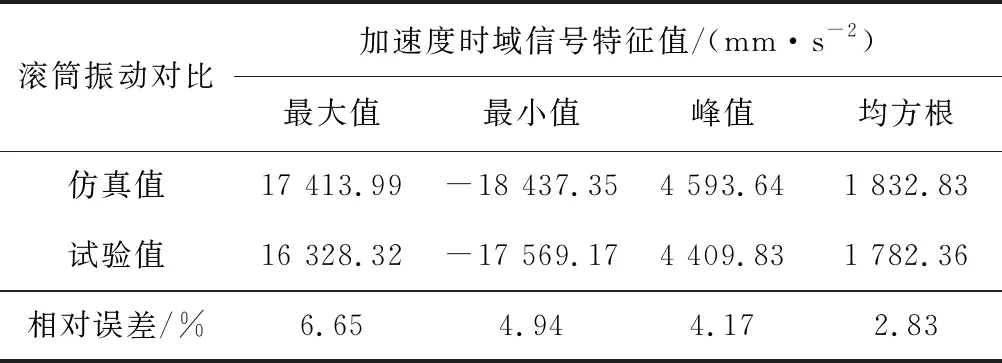
表7 滚筒截割阻力方向振动加速度时域信号特征值

AMEsim中有液压库及液压元件设计(HCD)库模块能够根据用户需求快速完成液压系统建模，同时解决基于经典控制理论研究液压系统动态性能差的问题，使研究更贴近工程实际。结合图1，基于AMEsim环境建立调高液压系统模型，组成元件参数设置见表8，模型如图9所示。

表8 元件参数设置

图9 采煤机电液比例调高液压系统AMEsim模型

以Simulink为多领域协同仿真主环境，基于AMEsim，RecurDyn和Simulink间接口模块将3者集成在一起，分别定义用于交换数据的输入、输出状态变量，将调高液压缸的活塞位移定义为输入，由 AMEsim 输入到 RecurDyn 液压缸的运动副中，RecurDyn将调高油缸作用力作为输出输入到AMEsim中的液压缸活塞上；通过将AMEsim输出的当前调高液压缸的活塞位移及与来自Simulink决策的调高液压缸的活塞位移目标值的差值输入至控制器，输出实现调高液压系统自适应调整的电信号，控制阀口开关及开口大小，提供给调高油缸稳定的流量以推动油缸活塞移动，使摇臂及滚筒实现升降，其中基于Simulink的自适应调高控制系统模型的建立将在第3节详细介绍，在此不多做赘述。据此实现采煤机自适应调高机-液-控一体化系统模型的构建，如图10所示，其中，为滚筒转速，r/min；为采煤机牵引速度，m/min；为滚筒截割阻力方向的振动加速度实时值，mm/s；为EDEM模型输出的煤岩颗粒对螺旋滚筒作用力，N；′为调高油缸活塞受力，N；为调高油缸活塞位移实时值，mm；为控制电液比例换向阀的电压信号，V。

图10 采煤机自适应调高机-液-控一体化系统仿真模型

3 采煤机自适应调高控制系统模型

3.1 采煤机煤岩截割状态感知分析

采煤机截割、破落煤岩过程中对采煤机运行状态的感知是实现采煤机自适应调高控制的前提，且要求感知过程具备实时性、快速性和准确性。在采煤机运动学参数一定的情况下，采煤机截割路径中所遇不同厚度顶板时，螺旋滚筒振动情况亦有差别，因此，螺旋滚筒振动情况能够反映被开采煤岩层的可截割性。选用连续3 s内的螺旋滚筒振动信号作为煤岩截割状态感知数据，根据滚筒振动加速度的时频谱图像能够实现煤岩截割状态的精准识别，且能够解决时域特征信号相似工况的区分问题，利用连续小波变换将表4所示的典型工况的滚筒振动加速度时域信号转换为时频谱图像以区分煤岩截割状态，如图11所示。

图11 不同煤岩截割状态的时频谱图像

由图11可知，截割4种典型工况下滚筒振动加速度的时频谱图像主频差异明显，因此可作为煤岩截割状态识别的图像数据样本。

3.2 基于Fancy PCA与Alexnet网络迁移学习的煤岩截割状态识别

近年来，机器视觉成为物品识别和分类的研究热点，文献[21-23]分别利用机器视觉、支持向量机、VGG16网络和迁移学习的思想、优化的LeNet-5网络对煤矸石进行分类，且文献[24]指出Alexnet是最适合于煤矸分选的深层神经网络，上述研究为煤岩截割状态识别提供全新手段。

3.2.1 基于Fancy PCA扩充样本数据库

为提高煤岩截割状态识别准确性，选用Fancy PCA方法扩充代表不同截割状态的原始时频谱样本，丰富原始数据库，提高模型的稳定性及鲁棒性，原始数据集是基于仿真获取的振动加速度时域信号经连续小波变换得到的时频谱图集合，每种工况的原始时频谱图样本均为30张，共计30×4=120张。

以工况1条件下滚筒振动加速度时频谱图为原始样本图像，基于Fancy PCA方法提取扩充的时频谱样本图像，并与原始样本图像进行对比，如图12所示。

由图12可以看出扩充样本与原始样本之间存在着很高的相似度，仍能够保持主频间相对位置关系，而在图像色泽、亮度等属性又略有差异，能够提高模型的泛化能力，可为煤岩截割状态的准确识别提供丰富的图像样本。

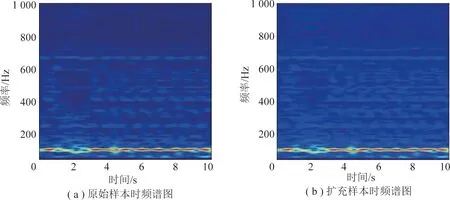
图12 时频谱样本与扩充样本之间的对比

3.2.2 基于Alexnet网络迁移学习实现煤岩截割状态识别

本文构建的Alexnet网络迁移模型主要由输入层、卷积层、池化层、全连接层、输出层组成，Alexnet具体网络结构如图13所示，卷积运算中，对于输入尺寸为×的图像，经过一个×大小的卷积核，步长为的卷积层操作，输出为

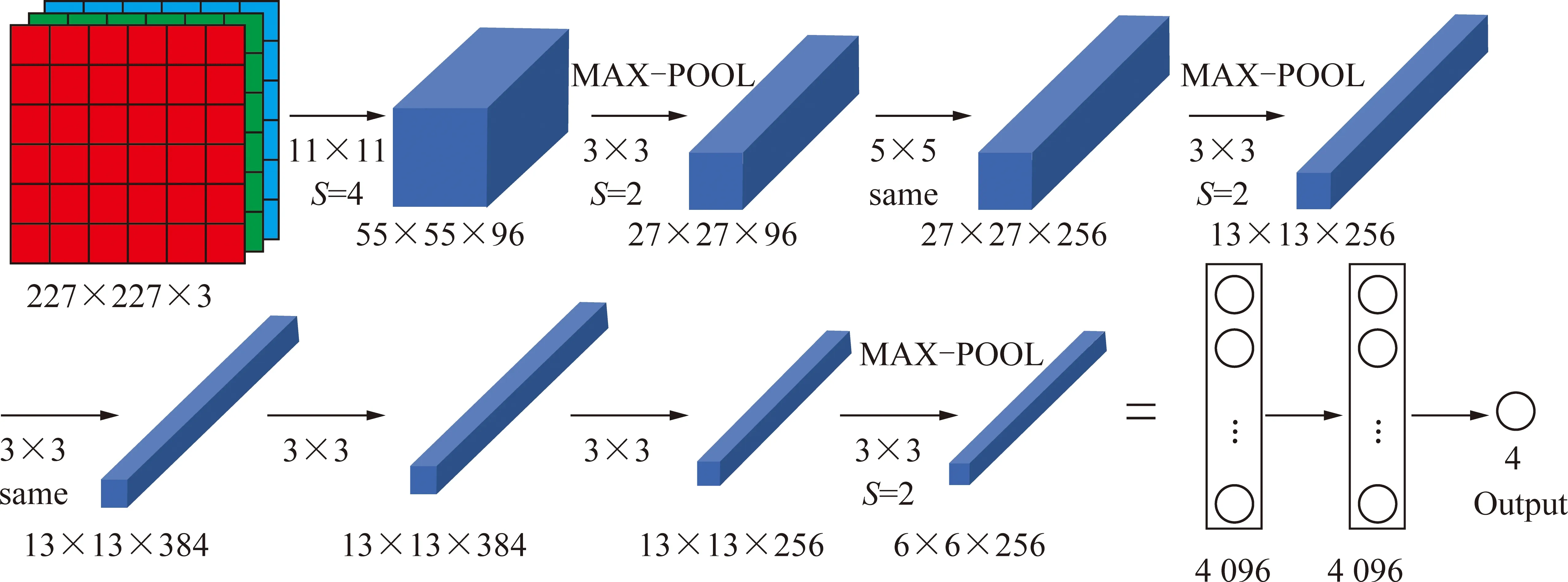
图13 Alexnet网络迁移模型结构

(9)

式中，为边界填充大小。

池化运算中，输出为

(10)

以多领域协同仿真获取的与基于Fancy PCA扩充的5 000×4张时频谱样本作为Alexnet网络输入，以与煤岩截割状态相对应的工况编号为输出，将4种代表煤岩截割状态的原始样本与扩充样本混合成的完整数据库按4∶1划分训练集和测试集，迭代次数设置为200，训练过程中其准确率的变化规律如图14所示。

图14 识别准确率

由图14可知随着迭代次数的增加，Alexnet网络迁移模型的识别准确率不断提升，当迭代次数达到140次左右时，识别准确率提升的速度缓慢，网络趋于收敛，识别准确率可为95.79%。

采用同样的手段重复进行了5次训练，得到的准确率分别为95.79%，94.89%，95.34%，96.18%和95.70%，得到模型平均识别准确率为95.58%。

3.2.3 识别模型与方法对比验证分析

分别选择经Fancy PCA进行数据样本扩充训练的Alexnet原始模型(Alexnet-FP)、Alexnet迁移模型(Alexnet-TL-FP)、VGG-16迁移模型(VGG-16-TL-FP)、GooleNet迁移模型(GooleNet-TL-FP)以及未经Fancy PCA进行数据样本扩充训练的Alexnet原始模型(Alexnet-NFP)和Alexnet迁移模型(Alexnet-TL-NFP)进行对比验证分析。根据控制变量原则保证各网络模型的参数设置相一致，经Fancy PCA进行数据样本扩充的样本数量为20 000，未经Fancy PCA进行数据样本扩充的原始样本数量为120，迭代次数为200，通过识别准确率及所消耗的识别时间为性能指标对其识别效果进行评价，结果见表9。

表9 不同模型下识别准确率及识别时间

对比表9中各模型的识别准确率及所需的识别时间可以发现：未经Fancy PCA进行数据样本扩充训练的Alexnet模型的识别准确率最低，仅为41.58%，在此基础上利用Fancy PCA进行数据样本扩充训练的Alexnet模型准确率升至48.07%，提升了6.49%，显然对原始数据样本扩充能够提升模型的准确率；Alexnet-TL-NFP和Alexnet-TL-FP相比于未经迁移学习的Alexnet模型的准确率显著提高，这是因为迁移学习能够将原模型上学习到的知识或模式迁移到所设计的新模型中，提高了模型的泛化能力，而Alexnet-TL-NFP的准确率低于Alexnet-TL-FP是因为将现有的小规模数据集应用于具有大型基础结构的网络中，容易产生过拟合，导致模型识别性能下降；VGG-16-TL-FP和GooleNet-TL-FP的准确率略高于Alexnet-TL-FP的准确率，但差距不大，造成这种结果的原因在于前两者与Alexnet-TL-FP相比具有更宽、更深的网络结构，提取特征能力更强；从所消耗的识别时间看4类Alexnet模型所消耗的时间接近，VGG-16和GooleNet迁移模型的识别时间远大于4类Alexnet模型。综上分析本文选择了经Fancy PCA数据样本扩充训练的Alexnet迁移学习模型对煤岩截割状态进行识别。

3.3 自适应调高控制系统模型的构建

自适应调高控制系统模型的构建需以其控制策略为指导，所制定的采煤机自适应调高控制策略如图15所示，结合Alexnet迁移学习网络的煤岩截割状态识别模型在Simulink中搭建采煤机自适应调高控制系统模型，如图16所示。

图15 采煤机自适应截割控制策略

图16 采煤机自适应调高Simulink控制系统模型

由图16可知，Simulink控制系统模型主要由信号处理模块(Signal processing)、时频谱图生成模块(Continuous wavelet transform System)、数据样本扩充模块(Fancy PCA System)、截割状态识别模块(Alexnet Transfer Learning System)、调高控制决策模块(Height Control decision)和DDPG高度调节模型模块(DDPG Height Adjustment Model)6个模块构成，其中时频谱图生成模块、数据样本扩充模块和截割状态识别模块已在第3.1节详细说明，在此不作赘述。信号处理模块实现对来自EDEM-RecurDyn仿真信息的预处理，利用Delay Line模块实现获取连续3 s内滚筒振动加速度时域信号，作为生成时频谱图的数据源；调高控制决策模块根据煤岩截割状态识别结果输出所对应的调高油缸活塞位移目标值；DDPG高度调节模型模块将DDPG控制器引入其中实现滚筒自适应调高。

3.3.1 基于DDPG的采煤机自适应调高模型的建立

DDPG是一种结合了基于值迭代和策略迭代的深度强化学习算法，具有复杂工况条件下自学习、自整定、自适应能力，非常适用于非线性、工况复杂且具有连续动作空间问题的采煤机自适应调高系统。受篇幅限制，其具体原理可参考文献[28]，在此不多作赘述。

将DDPG算法应用于采煤机调高液压系统，其整体结构框架如图17所示(图17中，为初始状态；+1为下一时间间隔后的状态；为智能体得到来自环境的即时奖励；为初始状态下随机采取某种动作；+1为在下一时间间隔后的状态下采取的最优动作；()为在状态下探索得到的目标动作函数；为状态动作价值函数；为critic网络目标函数)，框架主要由智能体(Agent)、奖励函数(Reward)、经验回放池(Experience Replay Buffer)和采煤机调高液压仿真模型(Simulation Model of Hydraulic High Adjustment of Shearer)4部分构成。智能体(Agent)由策略和学习算法组成，并分别通过用于生成动作的演员(Actor)网络和评价动作优劣的评论家(Critic)网络得以体现。

图17 基于DDPG算法的采煤机调高液压系统网络架构

为指导DDPG算法学习过程，设置奖励函数并从环境生成奖励信号，衡量Agent相对于给定的观察(状态)采取特定动作的有效性。

以基于DDPG算法的采煤机调高液压系统网络架构为指导建立并训练采煤机自适应调高系统模型。

(1)创建仿真环境。基于DDPG算法的采煤机自适应调高液压模型分别由Desired Height Level，Height Adjustment System，Signal Processing和RL Agent四大模块构成，其中Desired Height Level为液压缸活塞伸缩距离目标值模块，根据油缸活塞行程范围(150 mm)训练过程中随机选取的初始参数值应介于0～150 mm；Height Adjustment System为调高液压系统集成模块，由图9所示搭建的液压系统AMEsim模型转换为Simulink环境下的模型组成；Signal Processing为调高液压系统对深度强化智能体(Agent)的信号处理模块，将调高液压系统的液压缸活塞伸缩距离误差和液压缸活塞伸缩距离信号作为观察状态输入到RL Agent的Observation端口；以调高液压系统的液压缸活塞伸缩距离误差值为0作为RL Agent的截止条件输入至Isdone端口；以error值的大小作为奖励给予依据输入到RL Agent的Reward端口；RL Agent为DDPG深度强化智能体模块，基于DDPG算法以Reward端口和Observation端口数据为输入，在Action端口输出实现调高液压系统自适应调整的电压信号，最终得到基于DDPG算法的采煤机自适应调高液压模型，如图18所示。

图18 基于DDPG的采煤机自适应调高液压模型

(2)奖励函数的设计。奖励信号衡量Agent相对于任务目标的贡献，在训练过程中，Agent会根据收到的针对不同 “State-Action”组合的奖励来更新其策略。奖励函数分为离散奖励函数、连续奖励函数和混合奖励函数。本文结合调高液压控制系统设计了3类奖励函数，如式(11)～(13)所示。

离散奖励函数：

(11)

式中，为液压缸活塞伸缩距离误差，mm。

根据离散奖励函数的特点将奖励区间划分为||<01，01≤||<1，1≤||<5，5≤||<10，10≤||<17，17≤||<25，||≥25七个区间。结合式(11)可知，当误差超出区间时给予一个惩罚，且误差值越大，惩罚程度越严重，当误差在限定区间范围内时，为保证累计奖励最大值为负数，给予0的奖励。

连续奖励函数：

=-||

(12)

连续奖励函数是随液压缸误差值连续变化的奖励函数，亦是误差越大，惩罚越大。

混合奖励函数：

=+

(13)

混合奖励函数是综合考虑离散奖励函数和连续奖励函数的奖励函数。

(3)RL Agent的创建与训练。RL Agent使用critic价值函数表示近似长期奖励，利用actor策略函数来决定要采取的动作。创建一个具有观察和动作2个输入，以及一个用以评价动作优劣的输出的深度神经网络模拟critic网络，创建一个具有一个输入(观察)和一个输出(动作)的深度神经网络模拟actor网络，如图19所示。

图19 深度神经网络

采煤机工作过程中需根据复杂的煤层赋存条件对滚筒高度进行自适应调节，而其高度的调节依赖于调高液压缸活塞伸缩距离的精准控制，因此根据调高液压缸活塞伸缩距离范围设置式(14)所定义的重置功能函数，以随机化液压缸活塞伸缩距离目标值模块的参考值，保证Agent不定期地继续学习，不断更新控制策略以适应工况变化。

=150

(14)

式中，为0～1的随机数。

分别以，，为奖励函数信号对DDPG自适应调高控制模型进行训练，利用阶跃信号模拟调高液压缸活塞位移变化，比较基于3种奖励函数训练所得调高液压系统的控制性能，如图20所示。

由图20可知，相比于离散奖励信号和连续奖励信号训练的系统，混合奖励信号训练的系统响应速度更快，稳态误差更小，因此选择混合奖励函数作为训练智能体的奖励函数。

图20 不同奖励函数条件下系统控制性能

3.3.2 基于DDPG的采煤机自适应调高系统性能分析

分别利用模糊PID控制器及DDPG控制器实现采煤机调高液压系统的控制，并对两者控制效果进行对比分析。根据式(8)可得液压缸活塞收缩距离与螺旋滚筒下调高度之间的对应关系，见表10。根据表4中4种典型工况，并以工况1为例，基于搭建的采煤机自适应调高机-液-控一体化系统模型进行联合仿真，分别提取活塞位移跟踪情况及稳态误差、活塞运动速度和液压缸腔室流量变化3方面分析两者的控制性能，仿真结果如图21所示。

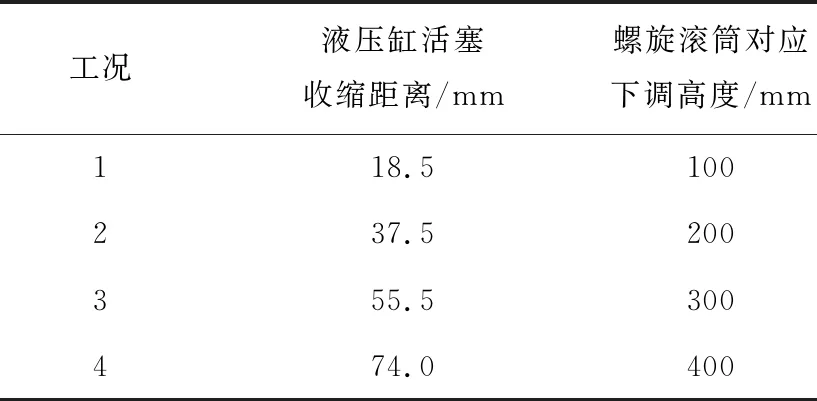
表10 液压缸活塞收缩距离与螺旋滚筒下调高度之间的对应关系

对比图21结果数据可以看出，基于模糊PID和DDPG控制的自适应调高系统在0～10.6 s时，活塞位移稳定在0 mm、活塞运动速度稳定在0 mm/s、液压缸流量稳定在0 L/min，但由于截割过程中负载的变化，其在稳定值附近有小幅波动，基于模糊PID控制的系统在初始时刻存在冲击，这对液压系统不利，而基于DDPG控制的系统初始时刻冲击较小，0～10.6 s处于调高前稳定阶段，基于模糊PID和DDPG控制的系统的位移稳态误差分别为0.2 mm和0.001 8 mm，且后者的活塞运动速度和液压缸流量控制更为稳定，在10.6 s接收到调高控制指令并开始调高，表明两者经0.6 s即感知到截割工况的变化，具有较快的响应速度；10.6～13.7 s处于调高阶段，经3.1 s左右活塞到达所设定的位置，在此过程中，活塞运动速度、液压缸有杆腔流量分别在6 mm/s、4.25 L/min左右波动，基于DDPG控制的系统波动更小；13.7～25.0 s处于调高后稳定阶段，基于模糊PID和DDPG控制的系统的位移稳态误差分别为0.32 mm和0.002 1 mm，且对比与调高前稳定阶段，模糊PID控制的系统的活塞运动速度和液压缸流量波动显著增大，而DDPG控制的系统则差别较小，表明后者具备更强的自适应性；综上述分析，显然DDPG控制器相比于模糊PID控制器的控制性能更优。

图21 模糊PID控制器及DDPG控制器性能对比

4 采煤机自适应调高系统联合仿真及性能分析

在Simulink控制系统模型中添加采煤机牵引速度=4.2 m/min、滚筒转速=90 r/min，调整滚筒高度至贴近顶板位置，以液压缸活塞缩回位移为正，伸出位移为负，设置仿真步长为0.05 s，对表4中4种典型工况进行EDEM-RecurDyn-AMEsim-Simulink多领域协同仿真，得到基于自适应调高控制下滚筒受载情况、液压缸活塞位移、运动速度及液压缸流量变化情况如图22～25所示，其中工况1的液压缸活塞位移、运动速度及液压缸流量变化情况在3.3.2节中已经给出，在此仅补充给出滚筒受载情况。

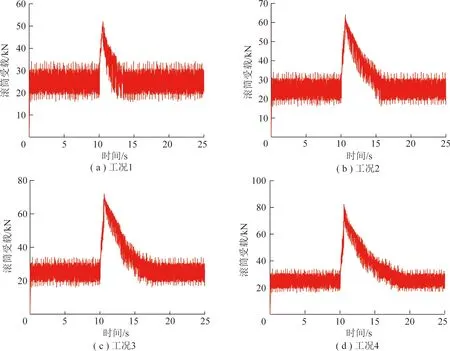
图22 滚筒受载变化情况

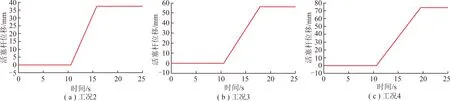
图23 液压缸活塞位移变化情况

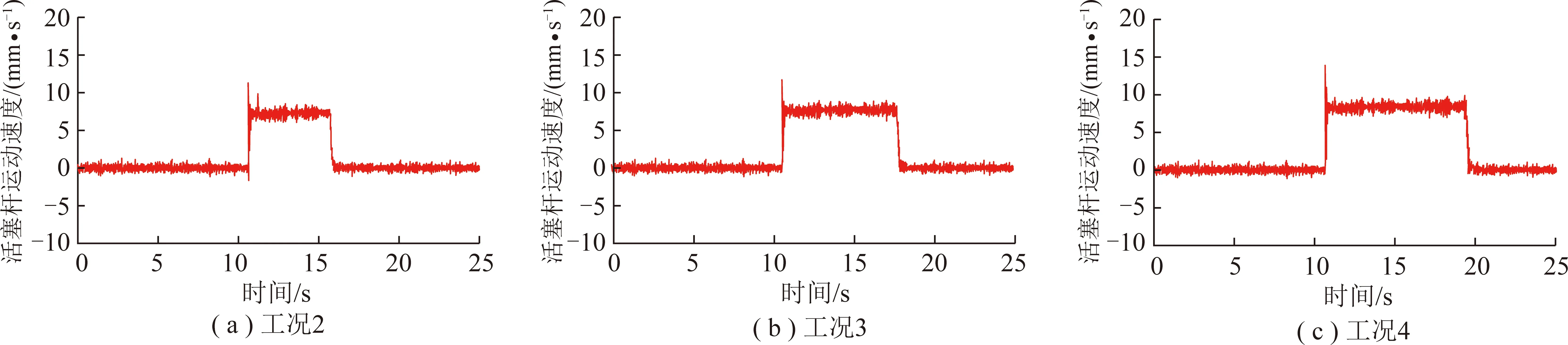
图24 液压缸活塞运动速度变化情况

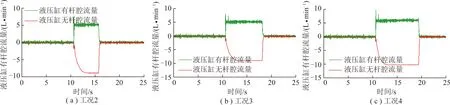
图25 液压缸腔室流量变化情况

由图22可以看出，在10 s左右之前4种工况条件下采煤机滚筒受载均在18 000～33 000 N波动，均值为25 500 N左右，仅变化趋势略有差别，这是由于滚筒初始位置不同造成的，由图23可看出4种工况条件下液压缸活塞位移几乎为0，说明此时液压缸活塞仅存在小幅度伸缩，滚筒高度亦处于初始高度截割工作中，由图24，25可看出活塞运动速度及液压缸腔室流量均在0 mm/s、0 L/min上下小幅波动，原因在于截割过程中由于煤岩体力学特性具有时变性和各向异性，致使作用在滚筒及截齿上的作用力亦是变化的，由此可以看出相比于以往将理想信号模拟截割阻抗进行系统性能分析的方法，多领域协同仿真能够较真实地模拟煤岩体实际截割破碎过程；在10 s左右时4种工况条件下采煤机滚筒受载突增，说明此时截割工况发生突变，但通过对比可知其增长幅度不同，分别经过0.57，0.61，0.60，0.56 s滚筒受载升至52 108，64 133，72 129，82 547 N，但此时液压缸活塞位移、运动速度和液压缸腔室流量仍保持初始状态；由图22，23可看出从10.6 s左右开始滚筒受载均下降，说明此时自适应调高系统仅经过0.6 s便感知到截割工况的变化，电液比例换向阀接到调控指令，推动阀芯并开启阀口，液压缸活塞开始缩回，表明系统具备较好的实时性和快速性，系统滞后时间短，4种工况条件下自适应调高系统分别经过3.1，5.2，7.3，8.9 s将液压缸活塞调整了18.497 9，37.501 7，55.498 4，74.001 9 mm，与目标位移值最大仅相差0.002 1 mm，与此同时滚筒受载随着滚筒高度的调节显著降低，并在滚筒高度调至目标值后恢复初始受载状态，表明此时滚筒已经避开顶板；由图24，25可看出在电液比例换向阀开启的瞬间活塞运动速度和液压缸有杆腔流量存在冲击，活塞运动速度最大分别可达9.02，11.31，12.24，13.81 mm/s，液压缸有杆腔流量最大分别可达6.21，7.72，8.24，9.71 L/min，由此可发现截割顶板厚度越大，对设备主要零部件冲击亦越大，阀口开启后液压缸活塞分别以6.0，7.2，7.6，8.3 mm/s左右的速度进行调节，液压缸有杆腔流量稳定在4.25，5.1，5.4，5.9 L/min，液压缸无杆腔流量逐渐增大后趋于稳定，调至目标位置后阀口关闭，液压缸位移恒定，滚筒高度保持不变，由此看出随着顶板厚度的增加，活塞位移目标值与当前位移值的增大，使得阀口开度适应工况变化，体现出基于DDPG控制的自适应调高系统具有良好的自适应能力。

5 试验验证

根据相似准则建立几何相似比为1∶2的自适应调高试验系统平台，计算得到采煤机结构参数、运动参数及时间相似比如表11、图26所示。

图26 自适应调高试验系统平台

表11 相似比的确定

试验平台主要包括试验台机液系统、上位机监控系统、操控台、机载测控系统及数据采集传输系统；其中试验台机液系统主要由试件夹持装置、截割装置(滚筒、摇臂、导轨、调高油缸、牵引液压缸)以及泵站等辅助元器件组成；滚筒高度采用定量泵-电液比例换向阀进行调节；上位机监控系统基于图形化编程语言LabVIEW开发，为了验证所提出的自适应调高策略，基于组件模型(COM)技术实现LabVIEW对自适应调高Simulink模型的调用，基于物联网技术以加速度传感器信号为主要分析对象，其他传感器信号为辅助监测信号，通过数据采集卡完成对其采集，并传输至上位机监控系统进行分析、处理和输出至交互式平台显示，根据识别结果向机载控制系统发出控制指令；将PLC作为机载测控系统的核心，基于OPC建立与上位机监控系统的通讯，以虚拟样机仿真调控策略为指导，结合接收煤岩截割状态识别结果对应的控制指令设计PLC控制程序，输出用以控制电液比例换向阀的电信号，并按比例转换成电磁力，从而改变电液比例方向阀的流量，实现对活塞伸缩速度的控制，自适应调高试验系统结构框图如图27所示。

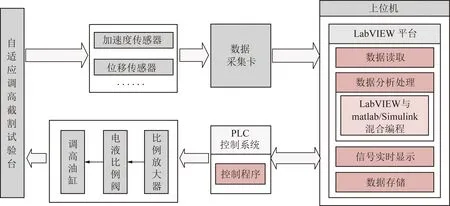
图27 自适应调高试验系统结构框图

基于兖矿煤业集团杨村矿4602工作面，根据相似准则推导相似夹矸煤岩性能参数，以工况2为例，将砂子、水泥、石膏、水按不同比例混合制作煤壁实体模型，保证相似煤壁在性能上与实际夹矸煤岩的一致性。

采用自适应调高试验系统平台进行试验，整理采集设备数据，获取试验条件下液压缸活塞位移、运动速度变化情况及两者相似反推数据，如图28，29所示。由图28及图29可以看出试验过程中液压缸活塞位移及其运动速度变化趋势与仿真过程基本一致，在图28中液压缸活塞位移试验值在0～8.8 s维持在0 mm左右，在8.8～13.12 s液压缸活塞位移由0 mm升至17.873 3 mm，在13.12～20.75 s液压缸活塞位移在17.873 3 mm上下小幅波动，结合表11中几何相似比取值情况能够计算出相似反推结果数据与仿真结果误差最大分别为4.68%；在图29中活塞杆运动速度试验值在0～8.8 s于0 mm/s左右小幅波动，在8.8～13.12 s活塞杆运动速度先增至6.75 mm/s后迅速降至4.15 mm/s左右小幅波动，在13.12～20.75 s活塞杆运动速度降至0 mm/s左右小幅波动，结合表11中牵引速度相似比取值情况能够计算出相似反推结果数据与仿真结果误差最大分别为3.97%。综上验证了提出的采煤机自适应调高控制策略的可行性与正确性。

图28 液压缸活塞位移试验结果及相似反推结果数据

图29 液压缸活塞运动速度试验结果及相似反推结果数据

6 结 论

(1)所提出的基于连续小波变换、Fancy PCA与Alexnet网络迁移学习相结合的方法能够实现煤岩截割状态精准识别，识别准确率可达95.58%，其为煤岩识别提供了全新的技术手段。

(2)利用DDPG深度确定性策略梯度算法能够实现对采煤机自适应调高系统调高过程的控制，且采用混合奖励函数对DDPG Agent进行训练效果最佳；通过与传统控制器控制的系统性能进行对比，得出基于DDPG控制的系统在响应速度、稳态误差及环境自适应性方面具备更优的控制性能。

(3)基于所搭建的自适应调高系统对4种典型工况进行联合仿真及性能分析，以仿真过程中滚筒受载、液压缸活塞位移、液压缸活塞运动速度及液压缸腔室流量4者的变化情况为系统性能评价指标，验证了自适应调高控制策略在多领域协同仿真中应用的可行性。

(4)利用物理试验验证了所提出的基于DDPG的采煤机滚筒自适应调高控制策略在实际应用中的可行性及多领域协同仿真结果的可靠性与准确性。