双空化射流中心体结构优化及破煤岩特性

涂翊翔，樊辰星，钱亦楠，王晓笋，康 勇，李 登

(1.武汉大学 水射流理论与新技术湖北省重点实验室，湖北 武汉 430072；2.武汉大学 动力与机械学院，湖北 武汉 430072)

煤层气(瓦斯)是在煤炭开采中形成的伴生气体，是一种十分重要的清洁能源。我国的煤层气资源存储量十分丰富，居世界第3，在国家能源战略中占有重要地位。随着中国煤矿开采规模的进一步扩大和开采深度的不断增加。煤层气治理和开发难度急剧增大，已严重威胁煤矿安全生产。抽采利用煤层气不仅可以减少煤矿瓦斯灾害事故，还对缓解能源危机具有重要作用。

我国目前采用的煤层气增产措施主要有钻孔卸压、水力压裂、水力割缝、水射流扩孔等。水射流技术由于其具有成本低、效果好、施工成功率高等优点，在煤层气开采领域受到广泛关注。刘勇等为了提高瓦斯抽采率，提出了磨料空气射流破煤增透措施，利用LS-DYNA对磨料空气射流冲蚀煤岩体进行了数值模拟，分析了射流扩散角和磨料的形状特性对煤岩体冲蚀的影响规律，并通过实验验证了其冲蚀模型准确性。李晓红等在瓦斯抽采中利用高压水射流钻孔，通过岩石损伤模型数值模拟了煤岩损伤特性及裂隙场的演化规律，同时开采了低渗透率高压脉冲水射流瓦斯抽采系统，在抽采瓦斯实践中取得了成功。卢义玉等运用缩放型喷嘴探讨了影响空化射流破岩能力的主要参数，并指出空化射流冲击是一种有效的破岩方式。马东军等利用自制的射流破岩系统，对淹没和围压条件下多孔射流钻头的破岩钻孔规律进行了试验研究，考虑了不同水力参数(冲蚀时间、射流压力、围压等)和结构参数(孔眼数量和侧向孔眼扩散角)对破岩效果的影响，找出了最优喷距范围和最优扩散角范围。江红祥等通过SPH-FEA耦合算法建立高压水射流冲击破岩过程，模拟了水射流损伤破岩过程中岩石失效、裂纹扩展以及不同位置岩石单元的损伤程度随时间变化的过程，发现当入射角大于70°时损伤破岩效果较好。段新奇等研究了在高压水射流作用下水射流辅助机械截齿破岩和机械截齿单独破岩，利用LS-DYNA对旋转破岩进行了仿真研究，并指出高压水射流压力在岩石模型强度以下时，截割力峰值相对于机械截齿单独破岩有所降低，但比能耗没有明显降低。

针对空化射流所产生的空泡溃灭压力，国内外学者也做了较多研究，杨勇飞在对于近壁面空泡溃灭的仿真及实验研究时得到单空泡近壁溃灭时压力为2.5 MPa，此时空泡直径可达0.3 mm。吕炜在对27个空泡的仿真研究中指出，在驱动压强与无量纲距离一定的情况下，空化泡的尺寸不影响作用在壁面上的溃灭压强，作用在壁面上的溃灭压强与驱动压强具有较强的依赖关系。此外，CHAHINE等通过研究得出，作用在壁面上的溃灭压强与驱动压强的平方根呈线性关系，通过水锤理论将驱动压强与作用在壁面上的溃灭压强联系起来。

为了进一步提高水射流破煤岩效率并促进该技术在煤层气开发中的应用，笔者基于前期研究基础,提出了一种新型的双空化射流，通过同时产生剪切空化与绕流空化形成空化云来提高空泡群溃灭产生的能量，从而进一步提高水射流的打击力与切割破碎能力。

笔者首先通过数值仿真研究不同中心体嵌入深度及中心体形状下的射流速度及气含率，然后选取最优中心体结构下的双空化射流压力与气含率参数，再结合空泡群动力学理论与流场特性，运用流固耦合模型对射流破煤岩进行了仿真分析，并与普通射流的破岩效果进行对比。

1 数值模拟计算模型

1.1 几何模型

双空化射流发生原理与喷嘴结构如图1所示。该喷嘴由外喷嘴、内喷嘴和中心体组成。外喷嘴环形通入低压水，内喷嘴通入高压水，当高压水通过含有中心体的内喷嘴时，中心体尾部会出现较大的湍动能和脉冲速度，在中心体尾部产生低压区从而诱发绕流空化。同时，由于高压水与低压水在速度上的巨大差异，射流剪切层中产生明显的速度梯度，促进了空化泡的产生。

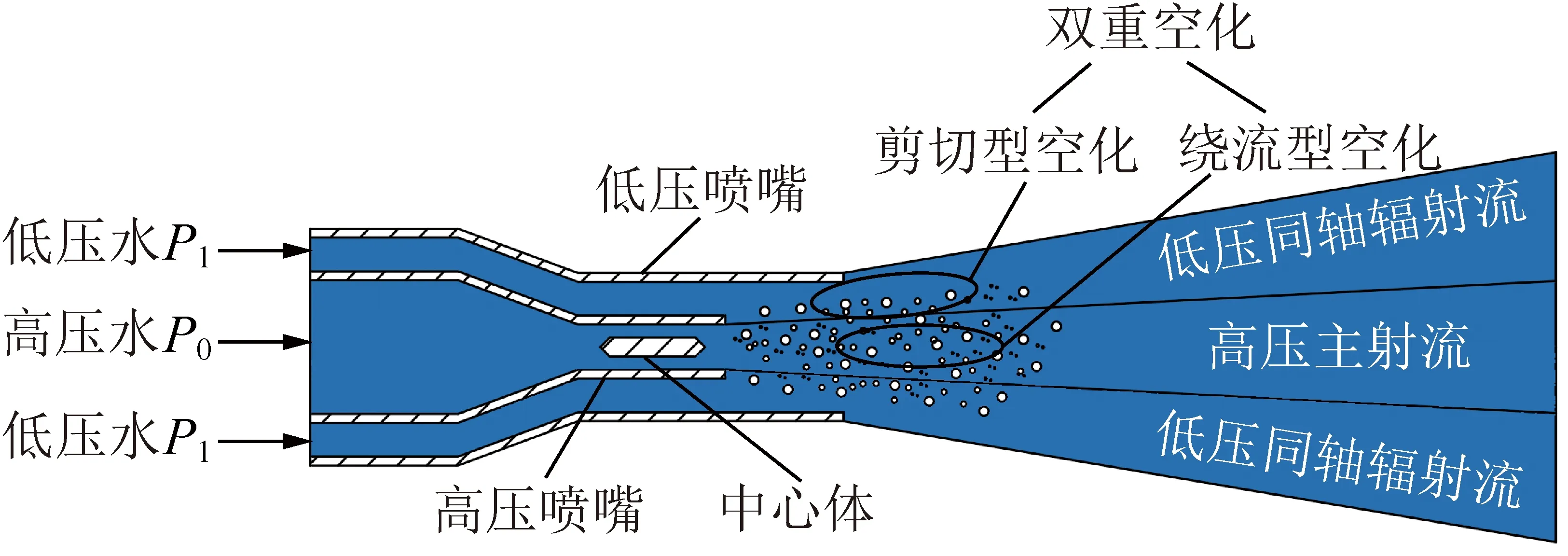
图1 双空化喷嘴结构与原理示意

双空化喷嘴的结构参数如图2所示。内喷嘴入口段直径=6 mm，内外喷嘴入口圆柱段长度=5 mm，内喷嘴出口圆柱段长度=5 mm，直径=2 mm，内外喷嘴径向间距=1.5 mm，出口轴向间距=2 mm，中心体长度=3 mm，直径=1 mm，收缩角为20°，笔者主要研究不同嵌入深度以及不同中心体形状下双空化射流性能。图3为不同中心体形状结构示意。根据廖松、邓松圣等前期对中心体喷嘴的研究，本文研究的中心体采用半球柱型以及90°锥形2种结构形式，为区分中心体结构的不同，沿着射流流动方向，对中心体前端用A来表示，对中心体末端用B表示，中心体形状用A-B表示。

图2 喷嘴结构参数

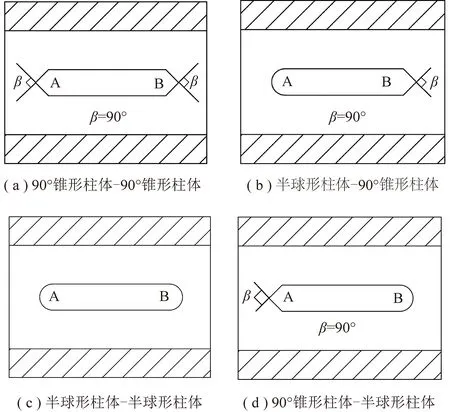
图3 不同形状中心体结构示意

1.2 控制方程

流场计算涉及到气液两相的混合流动，且属于湍流流动，同时由于绕流空化与剪切空化双重空化的发生，因此选用多相流中的Mixture混合物模型。该模型适用于各项速度不均等的多相流模拟，且较VOF模型和Eulerian模型更有助于收敛。

混合模型的连续性方程：

(1)

式中，为混合物密度，kg/m；为时间，s;为平均速度，m/s。

在进行射流计算时，标准-模型对于高速流动的仿真往往达不到预期的精度，而RNG-模型在方程中增加了一个附加项，在计算速度梯度较大的流场时精度更高。同时RNG理论能够兼顾高、低雷诺数流动黏性，在湍流中关于旋涡的计算更为准确。相较于标准-模型，RNG-模型可以适应更多类型的流动，同时拥有更高的精度。故湍流模型采用RNG-模型。

RNG-模型输运方程(分别属于湍动能以及耗散率):

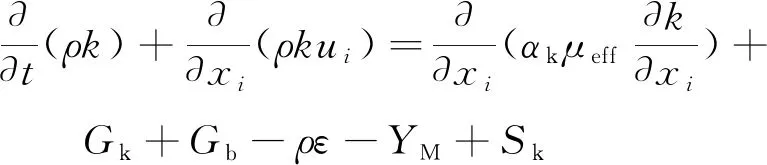
(2)

式中，为密度，kg/m；为不同输运物质的相，=1,2,3；为第相在其方向上的位移；为第相的流速，m/s；为有效磁导率；为平均速度梯度引起的湍流动能；为由浮力产生的湍流动能；为可压缩湍流中波动膨胀对总耗散率的贡献；为湍动能的库郎特数倒数;为用户定义的源项。

选用Schnerr-Sauer空化模型，控制方程用有限体积法进行离散，模拟采用基于压力的求解器，压力速度耦合采用SIMPLEC计算方法，离散格式采用二阶迎风格式。

1.3 网格划分与模型设置

本文提出的双空化喷嘴计算模型如图4所示。采用二维旋转对称模型，最大网格为0.2 mm，总网格数量为1.4×10。

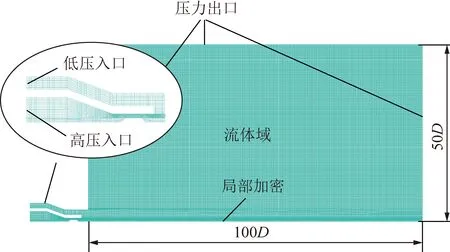
图4 计算模型

由笔者前期研究，最大网格尺寸取0.2 mm时已达到网格无关，因此取0.2作为计算网格大小。高压入口压力为20 MPa；低压入口压力为0.4 MPa。流场出口为大气压，为0.101 MPa。由于在中心体以及高低速射流交汇处出口区域，水和外界介质存在强烈的相互作用，对该处网格进行了适当加密。

2 数值模拟结果与流场特性分析

2.1 不同嵌入深度l的影响

嵌入深度分别取0.5，1.0，1.5，2.0 mm，其对气含率影响如图5所示，对速度影响如图6所示。

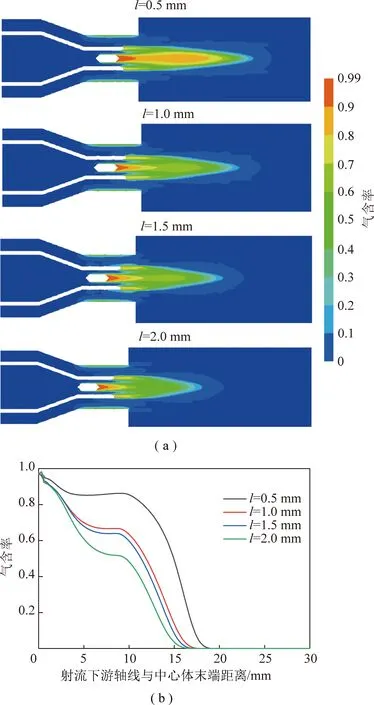
图5 不同嵌入深度下喷嘴射流流场气含率分布和对比

图6 不同嵌入深度下喷嘴射流流场速度分布和对比

由图5可以看出，射流经出口圆柱段后绕过中心体末端产生旋涡，形成负压区，同时射流绕过中心体末端后诱发了一个舌型空化气含区，并沿着轴心线向外扩散。随着嵌入深度的增加，喷嘴的空化区逐渐变小，这是因为中心体尾流诱发形成的空化泡在到达出口端面前就逐渐溃灭，从而使得在流场出口处形成的空化泡减少。从图5(b)可以看出，在距中心体后端10 mm处，=0.5 mm时的气含率接近0.9，而=1.0，1.5，2.0 mm时气含率分别为0.70，0.65，0.52。相比之下，=0.5 mm时双空化喷嘴具有更好的空化性能。随着距离中心体长度的增加，相较于另外3个嵌入深度，=0.5 mm时空化云长度更长，约在19 mm处才逐渐消失。这说明中心体嵌入深度对空化效果的形成有重要的影响，嵌入深度越小，空化作用的有效距离越大。在=0.5 mm时，产生的空化区域最大，空泡的扩散更有利。

由图6可知，随着中心体嵌入深度的增加，双空化喷嘴射流轴心线上的最大速度出现越早。尽管=2.0 mm时射流可达到的最大速度最高，但不同中心体嵌入深度的双空化喷嘴速度变化趋势基本趋于一致，在离中心体30 mm处逐渐趋于重合。此时=0.5 mm稳定速度最高，可以看出嵌入深度的改变对射流轴心线上的速度影响不大。

由上述对气含率分布和速度分布对比后可知，通过减小嵌入深度可以增大空化气含区，空化作用的有效距离也就越大，在=0.5 mm时空化作用效果最好。

2.2 不同中心体形状的影响

根据2.1节结果，取=0.5 mm，改变中心体前端和末端形状为90°锥形-90°锥形、半球-90°锥形、半球-半球和90°锥形-半球。中心体形状对气含率影响如图7所示，对速度的影响如图8所示。

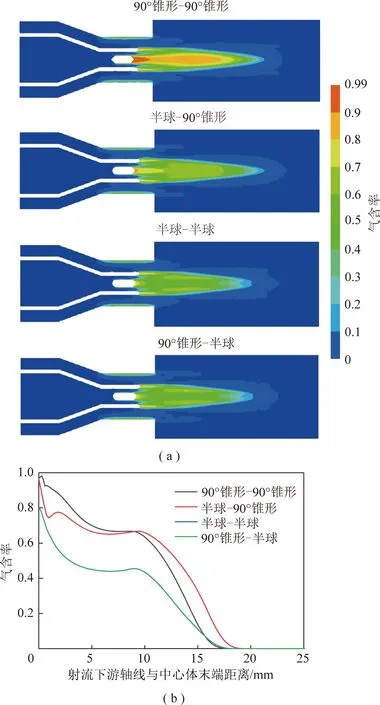
图7 不同中心体形状下喷嘴射流流场气含率分布和对比

图8 不同中心体形状下喷嘴射流流场速度分布和对比

从图7(a)可知，与半球柱中心体末端相比，射流在90°锥形柱体末端条件下产生的空化区域更大，集束性更好。但射流在中心体末端为半球柱体时产生的空化区存在径向发散。这是因为半球形柱体所形成的边界层比90°锥形柱体形状所产生的边界层易脱落，漩涡沿轴心扩散的同时存在径向移动。

由图7(b)可知，总体来看所有中心体形状下射流的气含率都随位置的增大而减小。当与中心体末端面距离小于4 mm时，气含率快速减小；在4～10 mm时，气含率几乎保持不变；当大于10 mm时，气含率急剧减小，并在18 mm时降为0。与中心体末端面距离小于10 mm时，中心体为90°锥形-90°锥形的气含率最高。

对于90°锥形-90°锥形和半球-90°锥形，当射流绕过中心体末端产生回流，并沿着轴心不断扩散，回流作用逐渐减弱，且都在中心体附近出现低速区；而中心体末端为半球柱体时形成的低速区最小，中心体形式为90°锥形-90°锥形时的低速区比中心体为半球形-90°锥形的更大。射流的速度在中心体尾部出现一点微小波动后逐渐增大。

由图8(b)可以看出，末端为半球形柱体中心体的喷嘴轴心速度增长最快，中心体形状为90°锥形-90°锥形柱体相较于中心体形状为半球-90°锥形柱体轴心速度增长速度基本趋于一致，但最终速度略低。末端为半球形的2条曲线基本重合，说明前端无论为半球柱或90°锥形体时对其速度的影响并不大。对比图7(b)和8(b)可发现，速度的增长率慢有利于空化区域的稳定扩散。尽管中心体形状为90°锥形-90°锥形时达到稳定时速度最慢，但其气含率相较其余几种形式随位置变化降速更低，更有利于增加其空泡溃灭打击强度。

通过在不同中心体形状下对气含率及速度进行对比分析后，认为在中心体形状为90°锥形-90°锥形时双空化喷嘴性能更优。

3 空化射流破煤岩流固耦合分析

基于流体力学、弹塑性力学及岩石力学，将射流和煤岩看作互相接触的2个物体，并考虑射流与煤岩的特性，通过流固耦合罚函数算法进行双空化射流破碎煤岩的数值模拟。由于煤岩的破坏主要由空泡溃灭时产生微射流和冲击波的强大冲击作用所致，因此利用空泡群动力学理论，将射流的冲击压力与空泡溃灭压力综合求得煤岩所受总压力，按Bernoulli方程将其转化为对应的速度参数，得到射流冲击煤岩的速度。

为了便于研究，对模型进行如下假设：① 岩石为各向同性连续介质，忽略孔隙介质的影响；② 射流以恒定速度水平冲击岩石。

3.1 流固耦合模型建立

3.1.1 不同靶距下射流冲击特性

为研究双空化喷嘴中空泡群溃灭压力与冲击波强度分布模型，计算其空化射流冲击压力，结合2.1，2.2节已求得的双空化喷嘴优化参数进行不同靶距条件下的冲击仿真，结果如图9所示，以中心体末端位置为坐标原点。

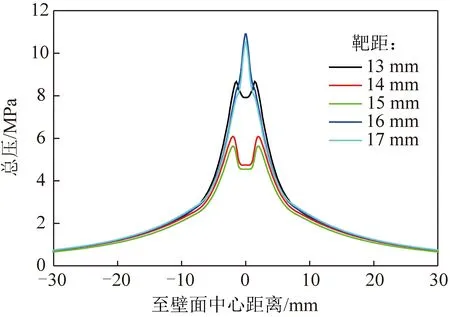
图9 双空化喷嘴冲击仿真

3.1.2 基于群泡溃灭动力学理论的空化冲击力计算

根据JOHNSON等研究了等温压缩条件下连续射流与空化射流冲击力之间的关系，得出：

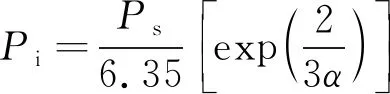
(3)

式中，为空化射流冲击压力；为连续射流冲击压力；为液体内气相体积。

此后，由COON和RUDY用实验给出，当=1/6～1/10时，可得

=(86～124)

(4)

由式(4)可得射流在不同靶距下的冲击压力，液体内气相体积可由在第2章所得到的最优参数中心体双空化射流得到，如图5(b)所示。将各参数代入后求得当靶距为15 mm时，空化射流冲击压力最高可达155 MPa，约为28倍的射流冲击压力。

同时根据实际情况对Bernoulli方程进行修正，该式适用于在射流的轴线附近区域，用于计算射流的流速：

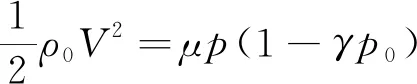
(5)

式中，为压缩性系数；为流体密度，g/cm；为流体速度，m/s；为入口压力，MPa；为喷嘴的溢流系数，为喷嘴收缩和速度系数的函数：

=∂(1-0184-02)

(6)

式中，收缩系数∂可以用喷嘴的几何参数来定义；为直径为处喷嘴出口圆柱段的长度，m。

将射流的等速核段定义为冲击段，由于射流核内存在着速度衰减，假设该段为一定靶距下射流冲击岩石的速度段。

此时该条件下有效半径(射流核半径)为

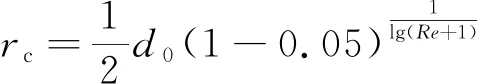
(7)

综合群泡溃灭动力学和射流冲击溃灭特性后，假设空化射流为具有一定半径下的等速核，对其进行射流破岩流固耦合仿真实验。

将各计算参数代入后可得：20 MPa驱动压强下的普通水射流经修正Bernoulli方程可得射流流速为63.24 m/s，而双空化射流喷嘴在引入空泡溃灭压力后总压可达155 MPa，换算后速度约为556.77 m/s。双空化射流与普通射流均取射流核半径=1 mm，并将所求的各参数代入破岩模型中进行求解计算。

3.1.3 空化射流破岩模型

空化射流破岩流固耦合模型采用1/4对称模型，岩石几何尺寸为40 mm×40 mm×60 mm，=1 mm。综合考虑射流冲击煤岩的非线性变形及高应变率特性，水本构方程用Gruneisen状态方程表示，空气状态方程采用多线性方程表示，岩石的材料模型选用J-H-C模型。采用MAT_NULL空材料模型来代表射流与空气域(图10)。在射流冲击段设置了较细密的网格，煤岩底端采用位移约束固定，由于瞬态冲击的作用会使网格严重变形并且产生高幅值的冲击波，对煤岩采用Lagrange算法，对射流采用Ale罚函数耦合算法。Ale方法继承了Lagrange方法的优点，能够较精确地描述结构边界的运动。同时具有Euler方法的优点，可以很好地克服单元严重畸变引起的数值计算困难。煤岩采用的J-H-C模型的材料参数见表1(为密度；为剪切模量；′为抗压强度；为最大静水拉伸强度；,分别为单轴试验中的压应力和体积应变)。

图10 流固耦合模型

表1 煤岩的模型参数

3.2 仿真结果分析

图11为普通射流与双空化射流分别在25，50，75，100 μs时的破岩效果对比，可以看出双空化射流对煤岩的冲击作用相较于普通射流更明显，且呈“锥形坑”状，与文献[26]结果吻合。

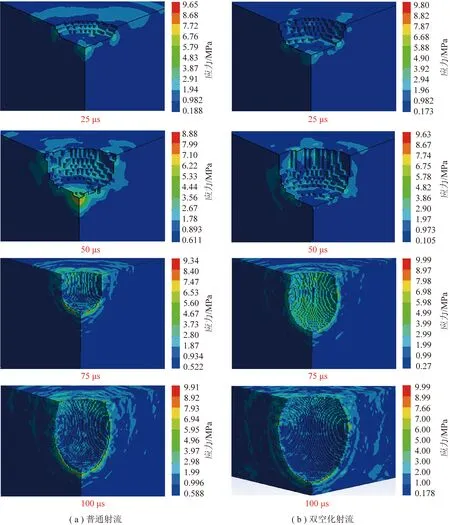
图11 射流破岩效果对比与Von-Mises应力示意

空化射流破岩的实质是由于空泡溃灭时产生的微射流和溃灭压强破坏煤岩，同时射流沿着煤岩表面裂纹进入煤岩内部，致使裂隙端部扩展从而破坏煤岩。在射流作用煤岩表面处受到射流的压应力与空泡溃灭所产生的溃灭压强，而未受到冲击的岩体与冲击处产生较大的剪切应力，从而受到破坏，形成初始的破碎坑。而距离射流冲击中轴线一定距离处，出现拉伸应力极值，使岩体产生裂纹，空化射流空泡溃灭时产生的微射流和溃灭压强对煤岩有强烈的破坏作用。随后，射流沿着煤岩表面裂纹进入煤岩内部，出现拉伸应力极值，致使裂隙端部进一步扩展。煤岩的损伤场在轴向和径向迅速扩展，深度和孔径都逐渐增大，而随着距离的增大，衰减极为迅速，双空化射流破岩过程中，由于空泡溃灭具有一段有效长度，当距离过大时，溃灭压强已无法对煤岩起到作用，同时由于射流的外沿损耗逐渐增大，流速降低，孔深、孔径的增长率迅速减小，促使形成“锥形坑”状。

图12为在双空化射流与普通射流冲击下煤岩破碎深度随时间的变化，同时与文献[27]中模拟的脉冲射流进行对比，可以看出，在50 μs前普通射流破岩冲蚀深度略优于脉冲射流，但在50 μs后却低于脉冲射流，2者的破碎深度和速度基本一致，这可能是由于在极短的时间内脉冲射流近似普通水流，2者特性相差不大。

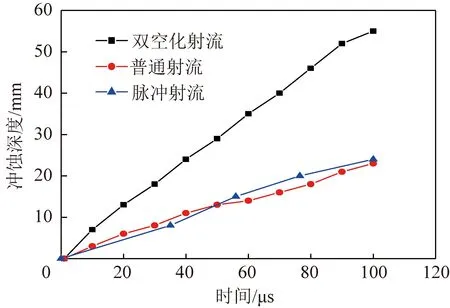
图12 煤岩破碎深度变化对比

双空化射流则表现出更高的破岩效率，在100 μs时破煤岩深度可以达到普通射流的2.4倍，这是由于双重空化增大了空化云的体积，从而使空泡溃灭时产生的冲击更大，作用于煤岩裂隙时破坏力更强，从而提高了破岩效率。

图13显示了普通射流与空化射流破岩冲蚀孔径特征。可以看出，在100 μs时双空化射流的破岩孔径为普通射流的1.3倍，这是由于双空化射流具备空泡云溃灭产生的巨大能量，可以对煤岩造成进一步破坏，煤岩的孔径进一步增大。同时，由于射流的“水锤效应”出现于冲击的开始瞬间，使得2者在10 μs都表现出极强的冲蚀能力，煤岩孔径呈线性增加，而在10 μs后2者的破岩效率开始降低，这是由于液体在破碎煤岩后的返回流分担了射流的很大一部分能量，但破岩孔径仍处于加大阶段。当作用的时间足够大时，破碎孔径不再明显增加。

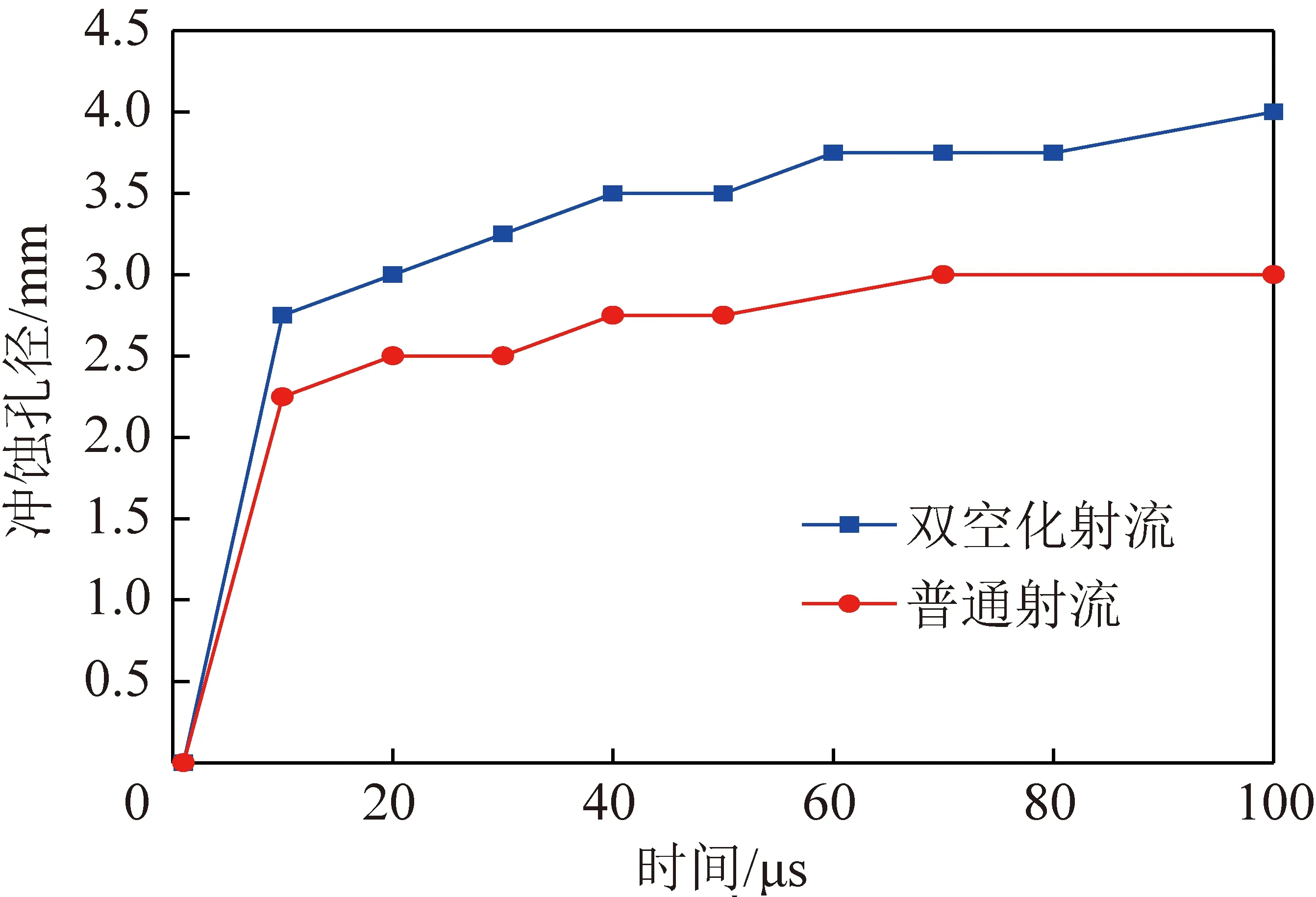
图13 煤岩破碎孔径变化对比

4 结 论

(1)通过对喷嘴内部中心体不同嵌入深度进行计算，发现随着嵌入深度的增加，喷嘴出口处的空化区逐渐变小，嵌入深度=0.5 mm时在距中心体末端10 mm处的气含率体积约为0.9，在距离为19 mm才逐渐消失，相较于其他3种嵌入深度，=0.5 mm产生的空化区域最大，对空化泡的扩散也更有利。

(2)针对不同的中心体形状，当中心体选用半球柱体时空泡存在径向发散的问题，而选用90°锥形柱体时的集束性更好，当末端为半球形时性能最差，因此在本文所选用的4种不同前后形状的条件下，前后形状为90°锥形-90°锥形中心体双空化喷嘴性能最优。

(3)结合群泡溃灭动力学，建立了空化射流破岩流固耦合模型，并将双空化射流与普通射流冲击煤岩破碎深度与破碎孔径进行对比，在100 μs时双空化射流冲蚀深度和孔径约为普通射流的2.4倍和1.3倍，随着时间的增长冲蚀孔径不再明显增加，而冲蚀深度不断增大，且与冲蚀时间呈线性关系。