基于混合输电线路下故障测距方法研究*

侯 伟 ，李宁

(1.国网北京市电力公司城区供电公司,北京 100010；2.国网北京市电力公司电缆分公司,北京 100020)

随着国民生活的不断提高,城市建设的步伐加快,用电负荷也越来越大,传统的架空线路不能满足城市的发展,也不符合城市现代化发展,因此采用了高压电缆线路,随之架空线路-高压电缆线路的混合输电线路越来越普及[1-2]。然而其故障也随之增多,也较为复杂[3-4],因此对混合输电线路的故障定位的研究具有重要意义。

目前,针对架空线路的故障定位方法主要有两种分别为阻抗法以及行波法[5-7]。阻抗法具有应用方便,且经济性高等特点,然而会受到系统阻抗或者过渡电阻等条件的影响,进而造成计算精度下降[8]。行波法能够有效降低输电线路运行方式、线路分布不均以及过渡电阻等条件的影响,然而针对混合输电线路仍受到不同线路参数的影响,进而造成精度降低[9-10]。

为了提高精度,一种基于双端行波原理的混合输电线路故障电位方法,通过对两侧行波进行检测能大致判断故障位置,但由于受到行波两端不同步造成的误差,将会影响其判断精度[11-12]。一种基于波速度归一法的混合输电线路故障判断方法被提出,该法通过将架空线路以及电缆线路的行波传播速度进行折算进而实现故障判断[13-14]。然而该方法实现困难且也会受到行波两端不同步的影响。此外,一些学者还提出了一种基于时间中点的双端行波故障测距算法以及一种基于分段补偿原理的混合线路双端行波故障定位方法等方法[15-17],然而上述方法测量精度均受到双端线路长度与时间不同步的影响,因此仍无法满足现阶段混合输电线路故障判断和定位的需求。

本文为了提高混合输电线路的故障测距效率,针对基于混合输电线路下故障测距策略进行了深入研究。首先深入研究了架空线路-电缆线路-架空线路结构的故障行波传播原理,针对故障点所在线路上以及对接处等情况提出了混合输电线路故障测距模型,通过搭建仿真模型,进而获得混合输电线路不同位置出现故障时的行波状态,并对所提故障测距策略的有效性进行验证,其结果具有一定的工程实际意义。

1 混合输电线路行波传播原理研究

1.1 故障行波传播原理

在由架空线路-电缆线路-架空线路的结构交替连接组成的混合输电线路出现故障后,其故障行波的传播路径示意如图1 所示。由于混合输电线路的变化行波阻抗不一样,所以其传输的速率也不尽相同,在电缆和架空线对接处的行波阻抗即为行波传递的转折点,因此在传播过程中遇到故障或者对接处均会产生行波折射以及反射[18]。

图1 中,Lo1和Lo2分别表示两段架空线路的长度,Lc则表示电缆线路的长度,K 和P 点分别表示了架空线路和电缆线路对接点,而F 点则表示故障点的位置,LMF则表示混合线路一段M 点和故障点F的距离。此外,参数tM和tN分别表示了故障点行波到达混合输电线路的两侧的时间,且i表示线路两端所收到的第i个波形,并令行波在电缆中传播速度为vc,在架空线路中传播速度为vo。

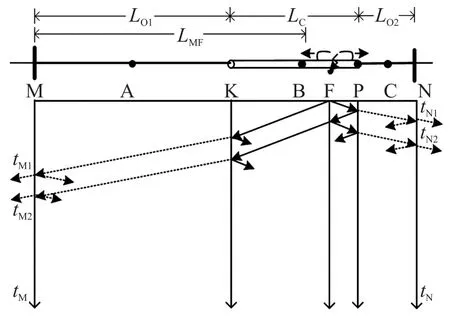
图1 混合输电线路故障行波的传播路径图

从图1 中能够得到,当线路出现故障后,其行波传播路径较为复杂。以图中故障点F 向混合输电线路的M 端进行行波传播过程为例进行分析。当故障出现时,其初始行波将会向M 端和N 端同时进行传播,其中向M 端传播过程中遇到对接点K 后,行波产生折射并继续向M 端传播,接着在M 端处出现折射以及反射,同时,另一侧故障行波向N 端传播过程中遇到对接点P 后,行波产生折射和反射,其中折射波继续向N 端传递,反射波则向故障点F 进行传播,并同样产生折射以及反射,其中该折射波将会继续向M端传播,并且在M 端同样发生折射与反射,反射波又会传播至故障点F 处,如此不断循环传递。

1.2 行波折射和反射特性

在架空线路-电缆线路-架空线路的混合线路结构中,行波的传播路径示意图如图2 所示。

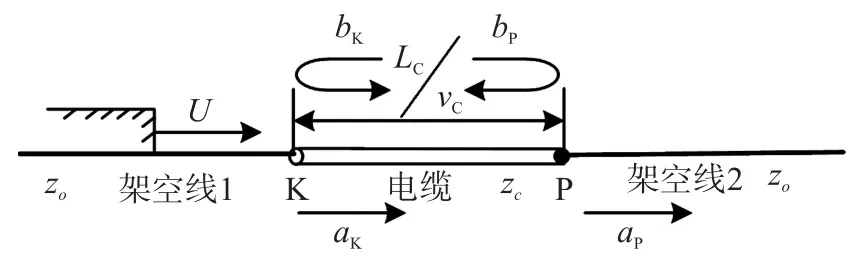
图2 行波的传播路径示意图

图中,参数Zc和Zo分别表示了电缆线路以及架空线路的阻抗,参数U表示行波的电压,而参数aK以及aP分别表示了行波在两个对接点的折射系数,而在两个对接点的反射系数分别为bK以及bP,根据反射和折射特点,其各系数分别被定义为:

若令两端的架空线路长度足够长,即其远处端的反射波还没传播至电缆和架空线路的对接处K和P,此时幅值U的电压行波从架空线路1 端向右传播,当其行波传播至对接点K 处时,行波出现折射波以及反射波,其中折射波会继续向右侧传播,在电缆线路上传播时间为Lc/vc,行波到达第二个对接点P 处,此时行波同样会产生反射波和折射波,其折射波继续沿架空线路2 传播,反射行波则是沿电缆向K 处传播,如此不断循环反复。令电压行波第一次到达K 处时作为初始时间,入射波方向设定为正方向,因此在P 处正方向上电压行波U(t)被定义为:

式中:参数n表示第n次反射。该式的第一项表示行波第一次从架空线路传播至电缆线路的电压行波分量,而第二项则表示在经过多次反射后再从P 处折射向架空线路2 端传播。同理能够得到其P 处正方向上电流行波I(t)被定义为:

此外,由于架空线路的波阻抗比电缆的大,所以行波在电缆中传播后,其幅值也会出现减弱。

2 混合输电线路故障测距方法

2.1 确定故障区间

针对故障出现在架空线路-电缆线路-架空线路的混合输电线路的不同位置,建立故障区间定位策略。在图1 的示意图上,假定三段线路MK(架空线路)、KP(电缆线路)、KP(架空线路)的中点A、B、C 三处以及在两个对接点K 和P 处出现故障时,故障行波传播至架空线路两端的时间差值进行序列整定,其公式定义为:

式中:参数ΔT1、ΔT2、ΔT3、ΔT4以及ΔT5分别表示了故障点在A、K、B、P 以及C 点出现故障时,其故障行波向两端传播时间的偏差。

令故障点传播至两端的时间为Δt,其值等于tM1和tN1的差值,当线路在不同地方出现故障时,其区间判定结果如表1 所示。

表1 混合输电线路故障区间判断

2.2 故障距离判断

针对故障出现在架空线路-电缆线路-架空线路的混合输电线路的不同位置时,即根据表1 对其故障与线路最左侧M 端的距离进行判断。

当故障出现在架空线路MA 区间内,在线路的M 端第二次接收行波是故障点的反射波,因此其故障点F 与线路最左侧M 端的距离被定义为:

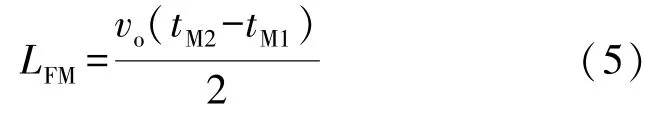
当故障点出现在第一段架空线路的中点A 点时,其在线路的M 端第二次接收行波是对接K 点与故障点反射波的累积波,且其F 与M 端的距离即为:

当故障出现在架空线路AK 区间内,在线路的M 端第二次接收行波是对接处K 点的反射波,因此其故障点F 与线路最左侧M 端的距离被定义为:

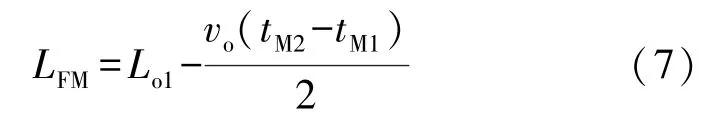
当故障点出现在第一段架空线路和电缆线路的对接处K 点时,其F 与M 端的距离即为:

当故障出现在电缆线路KB 区间内,在线路的M 端第二次接收行波是故障点的反射波,因此其故障点F 与线路最左侧M 端的距离被定义为:

当故障点出现在电缆线路的中点B 点时,其在线路的M 端第二次接收行波是对接P 点与故障点反射波的累积波,且其F 与M 端的距离被定义为:

当故障出现在电缆线路BP 区间内,在线路的M 端第二次接收行波是对接P 点的反射波,因此其故障点F 与线路最左侧M 端的距离被定义为:

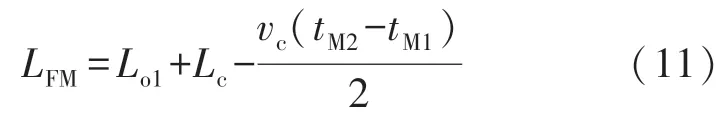
当故障点出现在电缆线路和第二段架空线路对接处P 点时,其F 与M 端的距离即为:

当故障出现在第二段架空线路PC 区间内,在线路的M 端第二次接收行波是故障点的反射波,因此其故障点F 与线路最左侧M 端的距离被定义为:

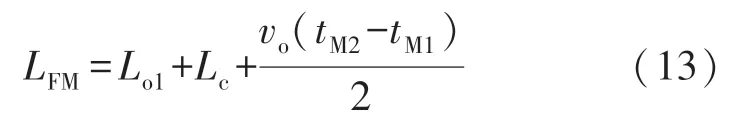
当故障点出现在第二段架空线路的中点C 点时,其在线路的M 端第二次接收行波是N 端与故障点反射波的累积波,且其F 与M 端的距离即为:

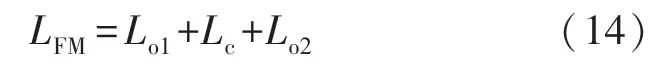
当故障出现在第二段架空线路CN 区间内,在线路的M 端第二次接收行波是N 端的反射波,因此其故障点F 与线路最左侧M 端的距离被定义为:

以江西工业贸易职业技术学院（以下简称江西工贸职院）为基地，与江西省粮油质量监督检验中心共同成立食品安全检测应用技术协同创新中心。双方共建实训场所，将创新中心打造成优良实验室规范（GLP），由江西工贸职院与企业实施订单培养，江西工贸职院与江西省粮油质量监督检验中心为江西省内粮食食品企业检验人员提供培训，并为粮油食品企业提供第三方检测服务。

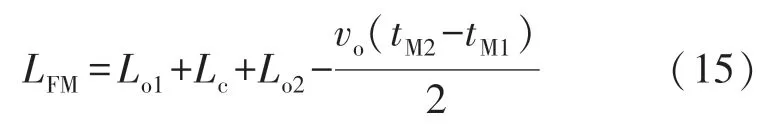
3 混合输电线路故障仿真模型建立

架空线路-电缆线路-架空线路结构的混合输电线路电路图如图3 所示,其中在各段线路上共设计了4 个故障点。

图3 混合输电线路故障电路示意图

通过PSCAD 软件构建其仿真模型,如图4 所示。主要参数设置为:架空线路的两侧M 与N 端的电压源均设定为500 kV,型号为LGJQ,4 分裂形式,半径为11.8 mm,裂相长度为450 mm,直流电阻大小为每公里0.108 Ω,电抗值大小为0.031 4 Ω；电缆结构则由6 层材料构成,从内向外分别是导体层、绝缘层1、保护层、绝缘层2、铠装层以及绝缘层3,厚度分别设定为18 mm、35 mm、36 mm、36.8 mm、38.2 mm 以及41.2 mm；系统频率设定为10 MHz。线路各段距离分别设定为:架空线路MK 距离和PN 距离分别为125 km 和10 km,而电缆段KP 距离则为30 km；并在各段内设定一个故障点,第一个故障点F1 在MK 区间,距离电缆M 端50 km；第二个故障点F2 在KP 区间,距离对接点K 为13 km；第三个故障点F3 对接点K 处；第四个故障点F4 在架空线PN 区间,距离对接点P 为5 km。

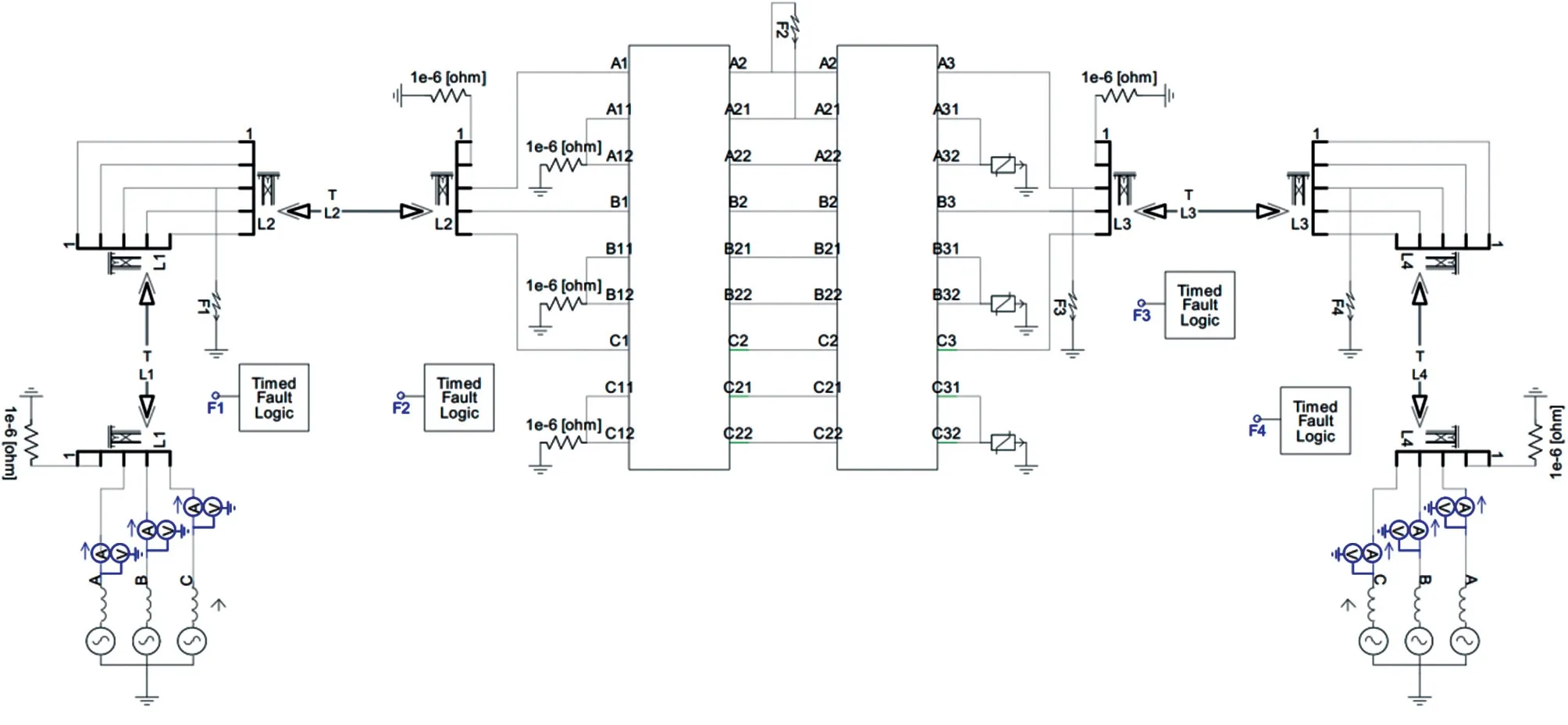
图4 混合输电线路故障仿真模型

4 仿真结果及其分析

4.1 金属直接接地故障仿真结果

(1)故障出现在F1 点

当架空线路-电缆线路-架空线路结构的混合输电线路各故障点在初始时刻(t＝0)出现金属性接地故障,且无过渡电阻,对线路M 端和N 端两端的故障相电流行波波形以及相电压行波波形进行采集。在故障点F1 点出现金属性接地故障时仿真结果如图5 所示。

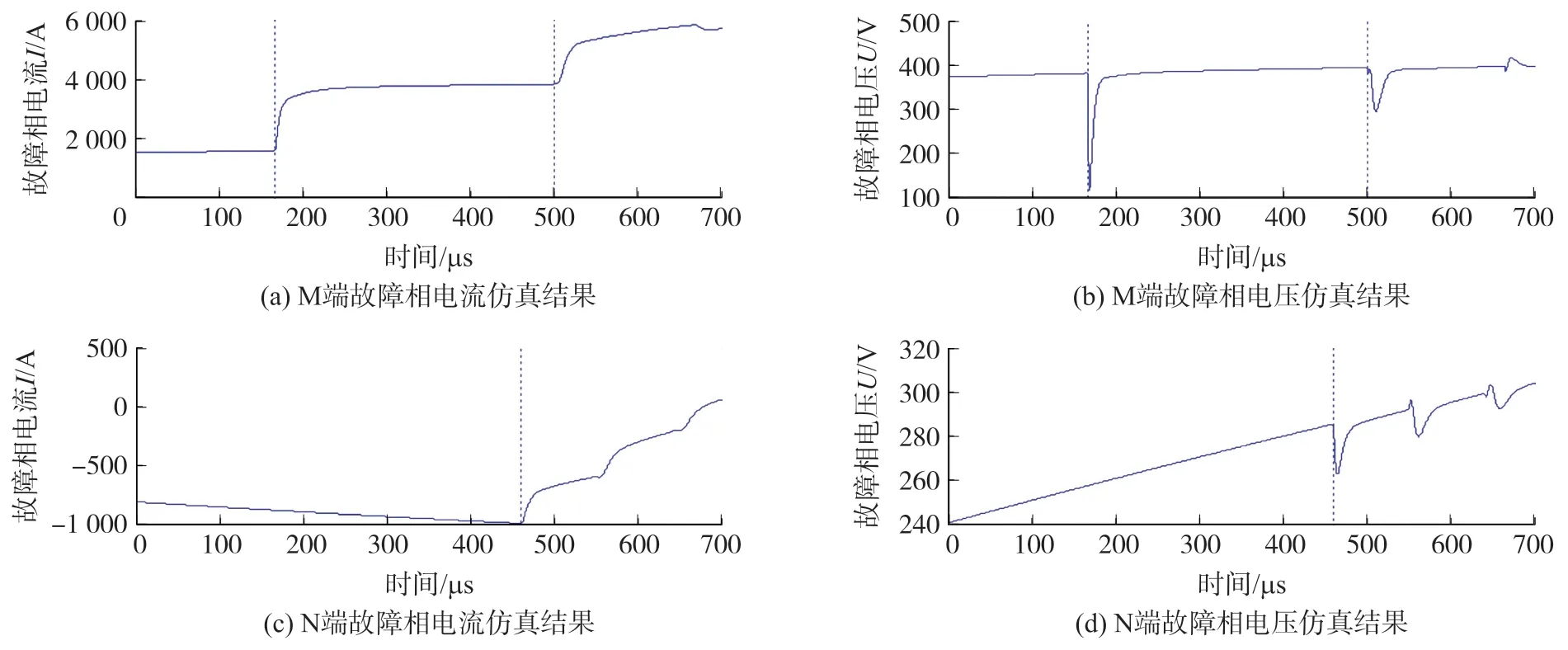
图5 故障点F1 的仿真结果

从图中能够得到,第一次到达线路M 端的时间tM1为168 μs,第二次到达线路M 端的时间tM2为502 μs,第一次到达线路N 端的时间tN1为457 μs。因此其Δt为-289 μs,此外根据式(4)可得参数ΔT1、ΔT2、ΔT3、ΔT4以及ΔT5的值分别为:

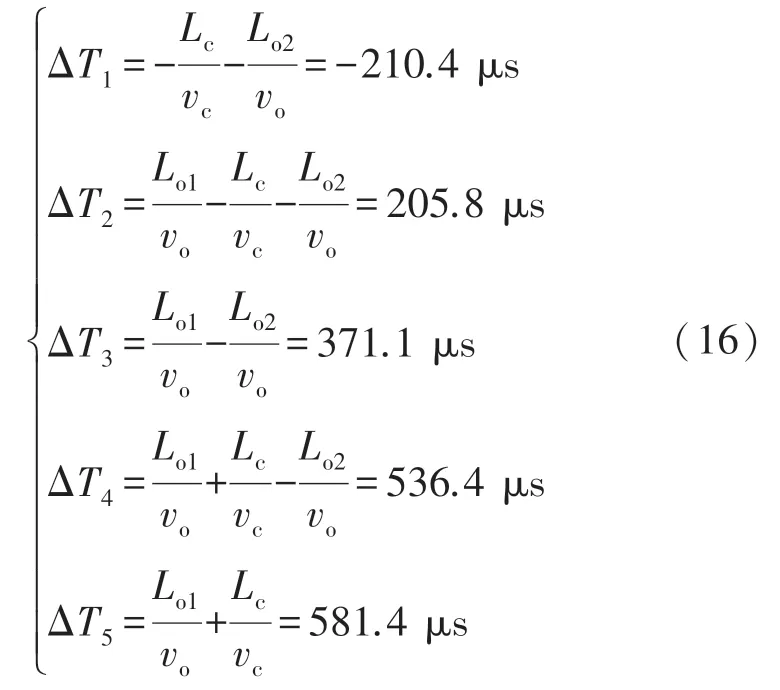
由于Δt小于ΔT1的值,因此判断其故障发生在MA 区间内,通过式(5)进一步得到其距离M 端的长度LFM为49.995 km,其计算结果与设定值的误差为0.005 km,表明该情况下此法能够较为准确判断故障位置。

(2)故障出现在F2 点

在故障点F2 点出现金属性接地故障时仿真结果如图6 所示。

图6 故障点F2 的仿真结果

(3)故障出现在F4 点

在故障点F4 点出现金属性接地故障时仿真结果如图7 所示。

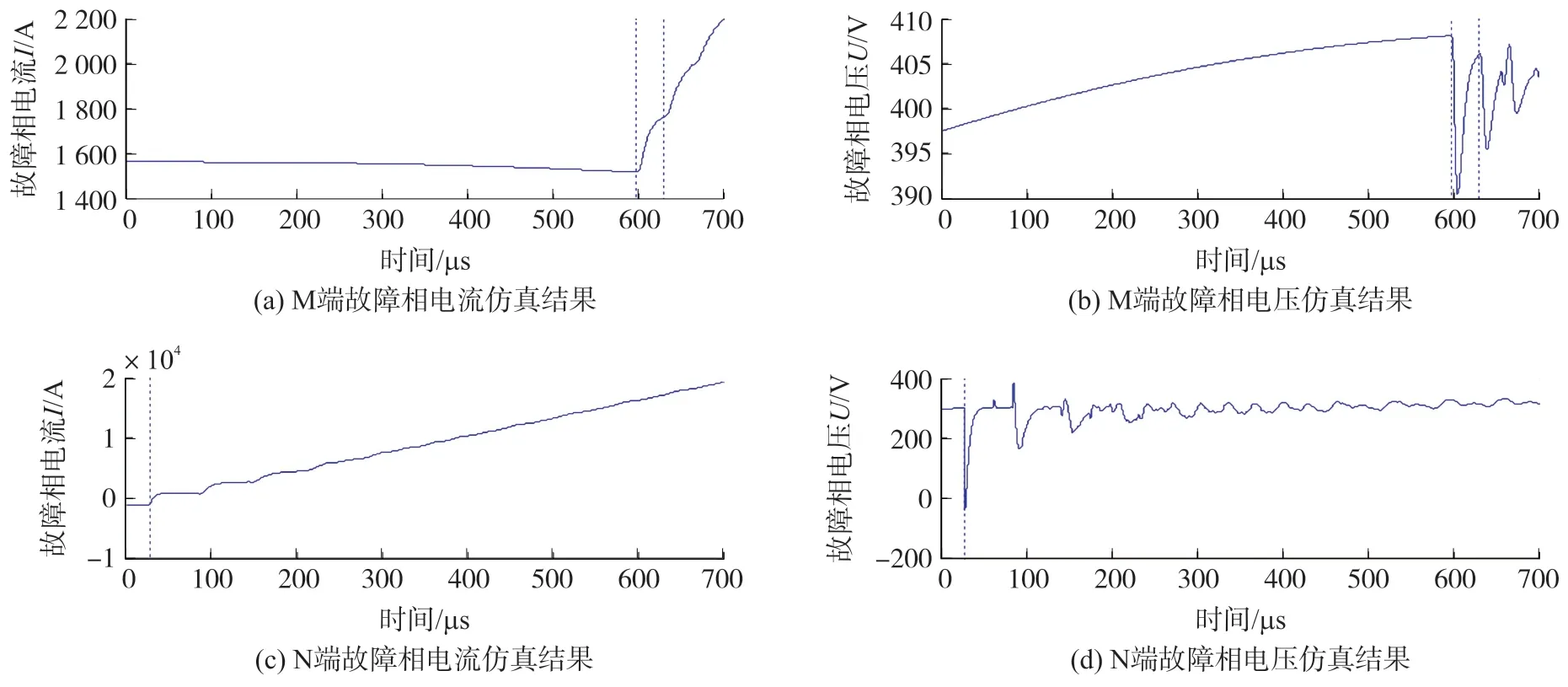
图7 故障点F4 的仿真结果

从图中能够得到,第一次到达线路M 端的时间tM1为599 μs,第二次到达线路M 端的时间tM2为632 μs,第一次到达线路N 端的时间tN1为29 μs。因此其Δt为570 μs,在ΔT4和ΔT5的区间范围内,即判断故障发生在电缆线路的PC 段区间,通过式(13)进一步得到其距离M 端的长度LFM为160.12 km,其计算结果与设定值的误差为0.12 km,表明该情况下此法能够较为准确判断故障位置。

(4)故障出现在F3 点

在故障点F3 点出现金属性接地故障时仿真结果如图8 所示。

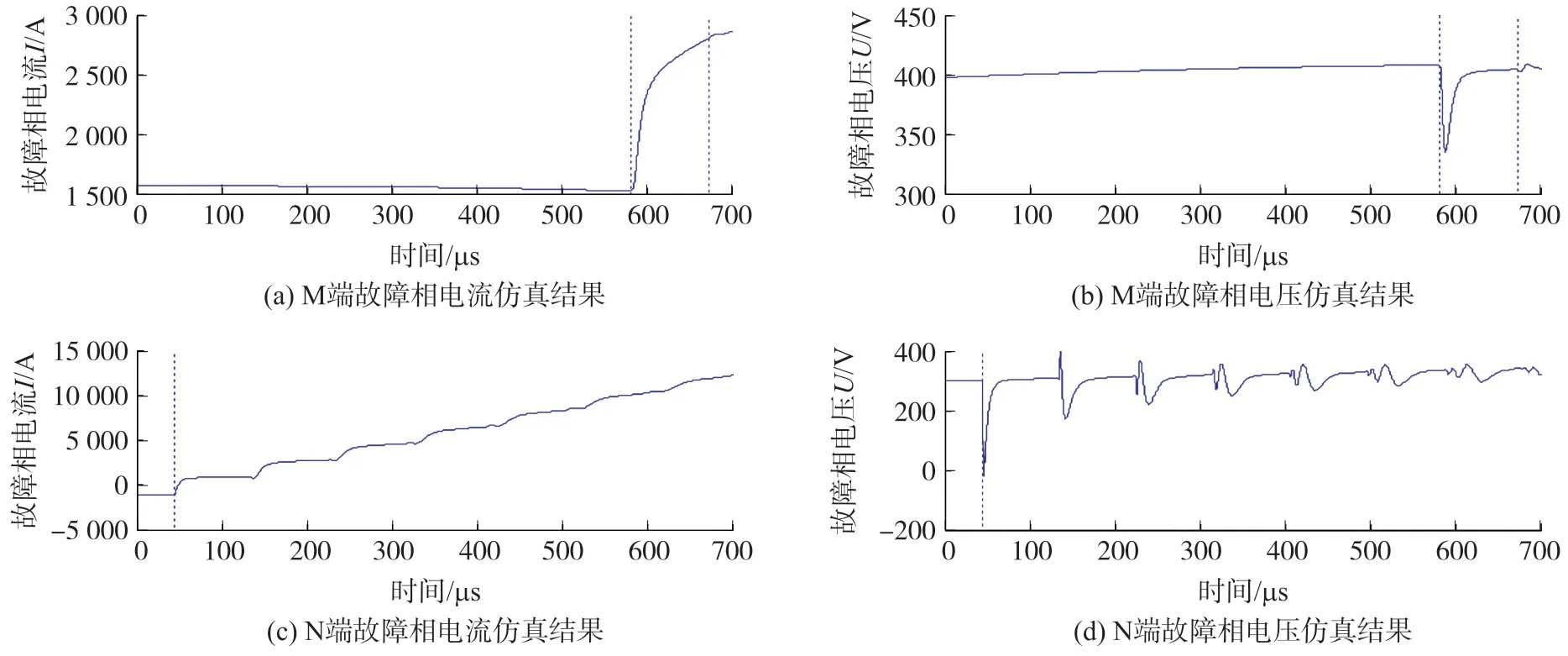
图8 故障点F3 的仿真结果

从图中能够得到,第一次到达线路M 端的时间tM1为582 μs,第二次到达线路M 端的时间tM2为672 μs,第一次到达线路N 端的时间tN1为46 μs。因此其Δt为536 μs。又由于存在的一定测量误差造成其Δt值和ΔT4的值虽然十分接近,但不完全一致。针对在对接处故障增加了一个判定条件,即若Δt的值远大于Δt和ΔT4的差值且其该差值小于1 μs,则可利用在对接处故障进行距离计算。通过式(12) 进一步得到其距离M 端的长度LFM为155 km,其计算结果与设定值一致,表明该情况下此法能够较为准确判断故障位置。

综合分析,当架空线路-电缆线路-架空线路结构的混合输电线路不同地方出现金属直接接地故障时,通过所提方法能够较为准确定位到故障位置。

4.2 经过渡电阻接地故障仿真结果

模拟混合输电线路各故障点在初始时刻(t＝0)出现经过60 Ω 的过渡电阻单相接地故障,并对线路M 端和N 端两端的故障相电流行波波形以及相电压行波波形进行采集。

(1)故障出现在F1 点

在故障点F1 点出现金属性接地故障时仿真结果如图9 所示。

图9 故障点F1 的仿真结果

从图中能够得到,第一次到达线路M 端的时间tM1为168 μs,第二次到达线路M 端的时间tM2为502 μs,第一次到达线路N 端的时间tN1为457 μs。因此其Δt为-289 μs,由于Δt小于ΔT1的值,因此判断其故障发生在MA 区间内,通过式(5)进一步得到其距离M 端的长度LFM为49.995 km,其计算结果与设定值的误差为0.005 km,表明该情况下此法能够较为准确判断故障位置。

(2)故障出现在F2 点

在故障点F2 点出现金属性接地故障时仿真结果如图10 所示。

图10 故障点F2 的仿真结果

从图中能够得到,第一次到达线路M 端的时间tM1为485 μs,第二次到达线路M 端的时间tM2为622 μs,第一次到达线路N 端的时间tN1为143 μs。因此其Δt为342 μs,在ΔT2和ΔT3的区间范围内,即判断故障发生在电缆线路的KB 段区间,通过式(9)进一步得到其距离M 端的长度LFM为138.01 km,其计算结果与设定值的误差为0.01 km,表明该情况下此法能够较为准确判断故障位置。

(3)故障出现在F3 点

在故障点F3 点出现金属性接地故障时仿真结果如图11 所示。

图11 故障点F3 的仿真结果

从图中能够得到,第一次到达线路M 端的时间tM1为582 μs,第二次到达线路M 端的时间tM2为672 μs,第一次到达线路N 端的时间tN1为46 μs。因此其Δt为536 μs。由于Δt和ΔT4的差值仅为0.4 μs,小于1 μs,则可利用在对接处故障进行距离计算。通过式(12)进一步得到其距离M 端的长度LFM为155 km,其计算结果与设定值一致。

(4)故障出现在F4 点

在故障点F4 点出现金属性接地故障时仿真结果如图12 所示。

图12 故障点F4 的仿真结果

从图中能够得到,第一次到达线路M 端的时间tM1为599 μs,第二次到达线路M 端的时间tM2为632 μs,第一次到达线路N 端的时间tN1为29 μs。因此其Δt为570 μs,在ΔT4和ΔT5的区间范围内,即判断故障发生在电缆线路的PC 段区间,通过式(13)进一步得到其距离M 端的长度LFM为160.12 km,其计算结果与设定值的误差为0.12 km,表明该情况下此法能够较为准确判断故障位置。

通过将经过渡电阻接地故障仿真结果和直接金属性接地故障仿真结果对比能够得到其经过过渡电阻后对线路故障行波的幅值有影响,对故障行波传播时间并无影响,因此通过所提方法仍能够较为准确定位到故障位置。

5 结论

本文研究了基于混合输电线路下故障测距方法。深入探究了架空线路-电缆线路-架空线路结构的混合输电线路故障行波传播原理,并基于行波原理提出故障位置区间定位以及距离计算方法。通过建立仿真模型模拟在混合输电线路不同位置出现金属性直接接地故障和经过渡电阻接地故障时,对线路两端的故障行波进行采集和分析。其实验结果表明:所提的基于混合输电线路下复合故障行波测距方法,能够较为准确地判断和定位到混合输电线路上出现两种故障时,其所在区间和距离。通过双端故障策略和在对接点故障策略相结合,有效弥补双端策略因长度与时间所引起的误差。此外,经过过渡电阻时,其故障波形只有幅值受到影响,对故障行波传播时间并无影响。该结果对混合输电线路故障更好的定位和测距有重要意义。